2022-2023学年广西河池市宜州区八年级（上）期中数学试卷（含解析）

2022-2023学年广西河池市宜州区八年级（上）期中数学试卷

一、选择题（本题共12小题，共36分）

1. 下列图案中不是轴对称图形的是．(    )

A.  B.  C.  D.

2. 下列各组线段中，不能组成一个三角形的是(    )

A. ，， B. ，，
C. ，， D. ，，

3. 已知的两边长为和，第三边的长为整数，则的周长是(    )

A.  B.  C.  D.

4. 如图，已知长方形窗框，，，，分别是其四条边的中点，为了稳固，需要在窗框上钉一根木条，这根木条不应钉在(    )

A. ，两点处
B. ，两点处
C. ，两点处
D. ，两点处

5. 若一个多边形的每一个内角都是，则该多边形是(    )

A. 六边形 B. 七边形 C. 八边形 D. 九边形

6. 在平面直角坐标系中，点与点的位置关系是(    )

A. 关于轴对称 B. 关于轴对称 C. 关于原点对称 D. 没有对称关系

7. 若等腰三角形的一边长为，周长为，则它的腰长为(    )

A.  B.  C. 或 D. 不能确定

8. 已知中，，则图中的度数为(    )

A.
B.
C.
D.

9. 如图，若从点出发，前进后向右转，再前进后又向右转，这样一直走下去，当第一次回到点时，所走的路程一共是(    )

A.
B.
C.
D.

10. 如图，在等边中，平分交于点，过点作于点，且，则的长为(    )

A.
B.
C.
D.

11. 如图，已知，下列条件中，不能判定≌的是(    )

A.  B.
C.  D.

12. 如图，等边三角形的边长为，、、三点在一条直线上，且≌若为线段上一动点，则的最小值是(    )

A.  B.  C.  D.

二、填空题（本题共6小题，共18分）

13. 十二边形的外角和是______ 度．
14. 已知点与点关于轴对称，则等于______．
15. 在中，，若，则为______
16. 如图，若，则______

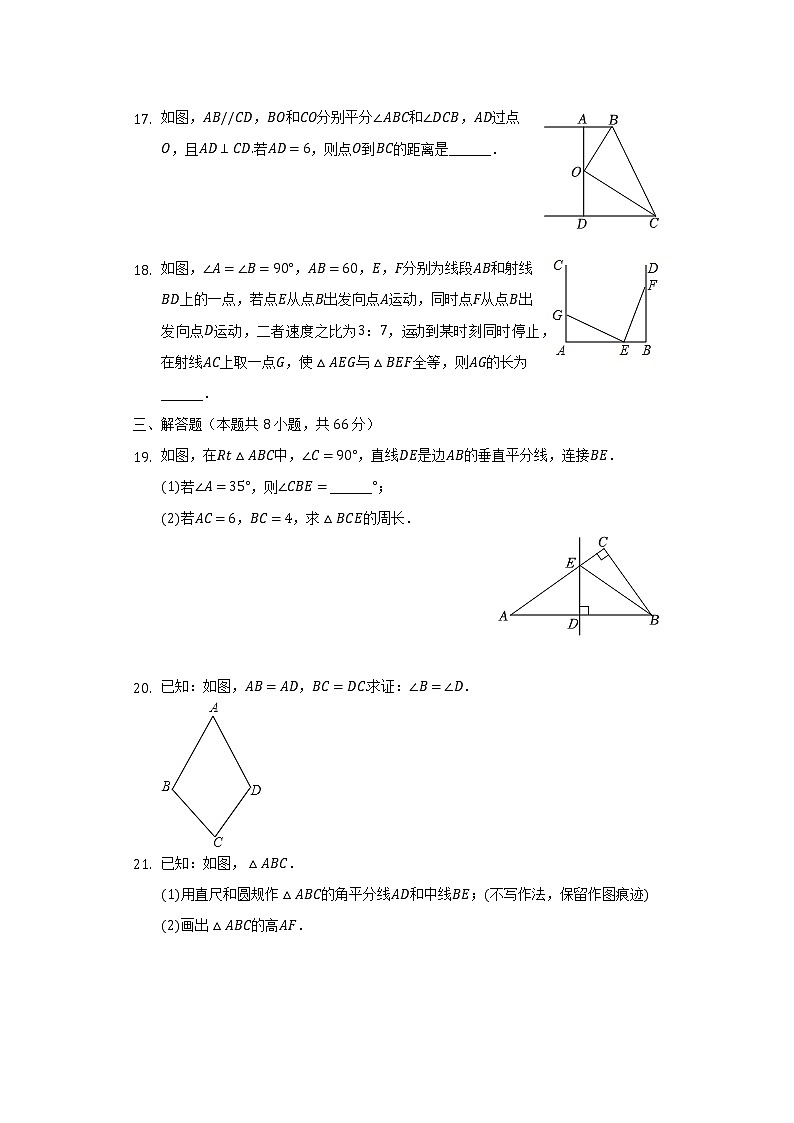
17. 如图，，和分别平分和，过点，且若，则点到的距离是______．

18. 如图，，，，分别为线段和射线上的一点，若点从点出发向点运动，同时点从点出发向点运动，二者速度之比为：，运动到某时刻同时停止，在射线上取一点，使与全等，则的长为______．

三、解答题（本题共8小题，共66分）

19. 如图，在中，，直线是边的垂直平分线，连接．
    若，则______；
    若，，求的周长．

20. 已知：如图，，求证：．
     
21. 已知：如图，．
    用直尺和圆规作的角平分线和中线；不写作法，保留作图痕迹
    画出的高．

22. 如图，三个顶点的坐标分别是，，．
    画出关于轴对称的，并写出点、、的坐标；
    在轴上求作一点，使的周长最小，并直接写出点的坐标．

23. 如图，树垂直于地面，为测树高，小明在处，测得，他沿方向走了米，到达处，测得，你能帮助小明计算出树的高度吗？

24. 如图，点在线段上，，，，平分．
    求证：于点．

25. 如图，，，垂足分别为，，，相交于点，求证：．

26. 如图，已知是等边三角形，点是边上一点．
    如图，以为边构造等边其中点、在直线两侧，猜想与的位置关系，并证明你的结论；
    如图，过点作，在上取一点，连接、，使得，猜想的形状，并证明你的结论．
    
    

答案和解析

1.【答案】 

【解析】解：、是轴对称图形，故此选项错误；
B、是轴对称图形，故此选项错误；
C、是轴对称图形，故此选项错误；
D、不是轴对称图形，故此选项正确．
故选：．
根据轴对称图形的概念求解．
本题考查了轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合．
 

2.【答案】 

【解析】解：、，故能构成三角形，不符合题意；
B、，故不能构成三角形，符合题意；
C、，故能构成三角形，不符合题意；
D、，故能构成三角形，不符合题意；
故选：．
根据三角形三边关系定理：三角形两边之和大于第三边，进行判定即可．
本题考查的是三角形的三边关系，掌握三角形三边关系定理：三角形两边之和大于第三边、三角形的两边差小于第三边是解题的关键．
 

3.【答案】 

【解析】解：的两边长为和，
第三边的取值范围是：，
第三边为整数，
第三边为，
周长为．
故选：．
根据三角形三边关系得出，任意两边之和大于第三边以及任意两边之差小于第三边，即可得出第三边的取值范围．
此题主要考查了三角形三边关系，根据第三边的范围是：大于已知的两边的差，而小于两边的和是解决问题的关键．
 

4.【答案】 

【解析】解：由三角形具有稳定性可知，这根木条不应钉在，两点处，
故选：．
根据三角形具有稳定性判断即可．
本题考查的是三角形的性质，熟记三角形具有稳定性是解题的关键．
 

5.【答案】 

【解析】解：一个多边形的每一个内角都是，则每个外角是，
该多边形是，
故选：．
由多边形的外角和是即可解决问题．
本题考查多边形的有关知识，关键是掌握多边形的外角和是．
 

6.【答案】 

【解析】解：点与点，横坐标相同，纵坐标互为相反数，
点与点的位置关系是关于轴对称．
故选：．
直接利用关于关于轴的对称点的坐标特点：横坐标不变，纵坐标互为相反数，进而得出答案．
此题主要考查了关于轴对称点的性质，正确记忆横纵坐标的符号关系是解题关键．
 

7.【答案】 

【解析】解：分两种情况：
当等腰三角形的底边长为时，
等腰三角形的周长为，
等腰三角形的腰长，
当等腰三角形的腰长为时，
等腰三角形的周长为，
等腰三角形的底边长，
等腰三角形的的三边长为，，，
，
不能组成三角形；
综上所述：它的腰长为，
故选：．
分两种情况：当等腰三角形的底边长为时，当等腰三角形的腰长为时，然后分别进行计算即可解答．
本题考查了等腰三角形的性质，三角形的三边关系，分两种情况讨论是解题的关键．
 

8.【答案】 

【解析】解：，
．
，
．
故选：．
先根据三角形内角和定理求得的和是度，再根据四边形的内角和是度，即可求得的值．
本题考查了三角形内角和定理和四边形的内角和定理．知道剪去三角形的一个角后得到一个四边形，根据四边形的内角和定理求解是解题的关键．
 

9.【答案】 

【解析】解：由题意知行走的路线是正多边形，边长是，每个外角是，
该多边形的边数是，
因此所走的路程一共是．
故选：．
由题意知行走的路线是正多边形，求出它的边数即可．
本题考查多边形的有关知识，关键是明白行走的路线是正多边形．
 

10.【答案】 

【解析】解：是等边三角形，
，，
，
，
，
，
，平分，
，
，
故选：．
先利用等边三角形的性质可得，，再利用垂直定义可得，从而利用直角三角形的两个锐角互余可得，然后利用含度角的直角三角形的性质可得，再利用等腰三角形的三线合一性质可得，即可解答．
本题考查了等边三角形的性质，含度角的直角三角形，角平分线的性质，熟练掌握等边三角形的性质是解题的关键．
 

11.【答案】 

【解析】解：由题知，，，
当时，≌，
故选项A能判定两个三角形全等；
，，
当时，≌，
故选B能判定两个三角形全等；
当，不能判定，≌，；
当，≌，
故选项D能判定两个三角形全等．
故选：．
从图中读取公共边的条件，结合每个选项给出的条件，只要能够判定两个三角形全等的都排除，从而找到不能判定两个三角形全等的选项C．
本题考查全等三角形的判定，注意一般三角形的“边边角”不能判定两个三角形全等，以及直角三角形的“”可以判定两个三角形全等．
 

12.【答案】 

【解析】解：连接交于点，
直线，且与关于直线对称，
，，共线，
，
，
，
，
，，
，关于直线对称，
当点与重合时，的值最小，最小值为线段的长，
故选：．
连接交于点，，关于直线对称，推出当点与重合时，的值最小，最小值为线段的长．
本题考查轴对称最短问题，等边三角形的性质等知识，解题的关键是学会利用轴对称解决最短问题，属于中考常考题型．
 

13.【答案】 

【解析】

【分析】
本题考查了多边形的外角和定理，多边形的外角和与边数无关，任意多边形的外角和都是，是基础题，需要熟记．
根据多边形的外角和等于解答．
【解答】
解：一个十二边形的外角和是．
故答案为：．  

14.【答案】 

【解析】解：由平面直角坐标系中关于轴对称的点的坐标特点：横坐标不变，纵坐标互为相反数，
可得：．
故答案为：．
利用平面内两点关于轴对称时：横坐标不变，纵坐标互为相反数，进行求解．
此题主要考查了关于坐标轴对称，解决本题的关键是掌握好对称点的坐标规律：
关于轴对称的点，横坐标相同，纵坐标互为相反数；
关于轴对称的点，纵坐标相同，横坐标互为相反数；
关于原点对称的点，横坐标与纵坐标都互为相反数．
 

15.【答案】 

【解析】解：中，
，，
．
故答案为：．
根据直角三角形两锐角互余，即可求出的度数．
此题考查了直角三角形两锐角互余的性质及度分秒的换算，熟记性质是解题的关键．
 

16.【答案】 

【解析】解：延长交于，

，
，
，
，
故答案为：．
延长交于，由三角形的外角的性质即可求解．
本题考查角的计算，关键是延长交于，应用三角形外角的性质．
 

17.【答案】 

【解析】解：过点作，垂足为，

，，
，
平分，，，
，
平分，，，
，
，
点到的距离是，
故答案为：．
过点作，垂足为，利用平行线的性质可得，然后利用角平分线的性质可得，进行计算即可解答．
本题考查了角平分线的性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
 

18.【答案】或 

【解析】解：设，则，因为，使与全等，可分两种情况：
情况一：当，时，
，，
，
解得：，
；

情况二：当，时，
，，
，
解得：，
，
综上所述，或．
故答案为：或．
设，则，使与全等，由可知，分两种情况：
情况一：当，时，列方程解得，可得；
情况二：当，时，列方程解得，可得．
本题主要考查了全等三角形的性质，利用分类讨论思想是解答此题的关键．
 

19.【答案】 

【解析】解：直线是边的垂直平分线，
，
，
，
，
故答案为：；
垂直平分，
，
．
根据垂直平分线的性质得，再根据三角形外角的性质得出的度数，即可求解；
根据垂直平分线的性质得出，再根据三角形的周长公式即可求解．
本题考查了线段垂直平分线的性质，等腰三角形的性质，熟练掌握线段垂直平分线的性质是解题的关键．
 

20.【答案】证明：连接，在和中，
，
≌，
． 

【解析】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：、、、判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．
连接，在和中，，，，通过可证全等，所以．
 

21.【答案】解：如图，、为所求；
如图，即为所求．
 

【解析】利用基本作图作的平分线得到，作的垂直平分线得到的中点，从而得到中线；
利用基本作图，过点作的垂线即可．
本题考查了作图复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了三角形的高、角平分线和中线．
 

22.【答案】解：如图所示，即为所求，各点的坐标分别为：，，．

如图所示，点即为所求，其坐标为． 

【解析】分别作出三个顶点关于轴的对称点，再首尾顺次连接即可得；
作点关于轴的对称点，再连接，与轴的交点即为所求．
本题主要考查作图轴对称变换，掌握轴对称变换的定义和性质，并据此得出变换后的对应点是解题的关键．
 

23.【答案】解：，，
，
，
，
又，
，
树的高度为米． 

【解析】本题考查了含角的直角三角形的性质，三角形的外角的性质有关知识，根据三角形外角的性质得到，根据等腰三角形的性质得到，由直角三角形的性质即可得到结论．
 

24.【答案】证明：，
，
在和中
，
≌，
，
平分，
． 

【解析】根据平行线性质得出，根据证≌，推出，根据等腰三角形的三线合一定理推出即可．
本题考查了全等三角形的性质和判定，平行线的性质，等腰三角形的性质等知识点，关键是求出，主要考查了学生运用定理进行推理的能力．
 

25.【答案】证明：，，
．
在和中，
，
≌，
．
在和中，
，
≌，
． 

【解析】由条件可证明≌，可得，再证明≌，可得．
本题考查全等三角形的判定和性质，解题的关键是熟练掌握基本知识，属于中考常考题型．
 

26.【答案】解：，理由如下：
和都是等边三角形，
，，，
，
≌，
，
，
；
是等边三角形，理由如下：
在上取点，使，连接，
则是等边三角形，

，，
，
，
，
，
，
，
，
，，
，
在和中，
，
≌，
，
，
是等边三角形． 

【解析】利用证明≌，得，再利用内错角相等，两直线平行即可得出结论；
在上取点，使，连接，则是等边三角形，再利用证明≌，得，从而解决问题．
本题主要考查了等边三角形的判定与性质，全等三角形的判定与性质，平行线的判定与性质等知识，作辅助线构造全等三角形是解题的关键．