

2022届江西师范大学附属中学高三5月三模数学(文)试题含解析
展开
这是一份2022届江西师范大学附属中学高三5月三模数学(文)试题含解析,共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
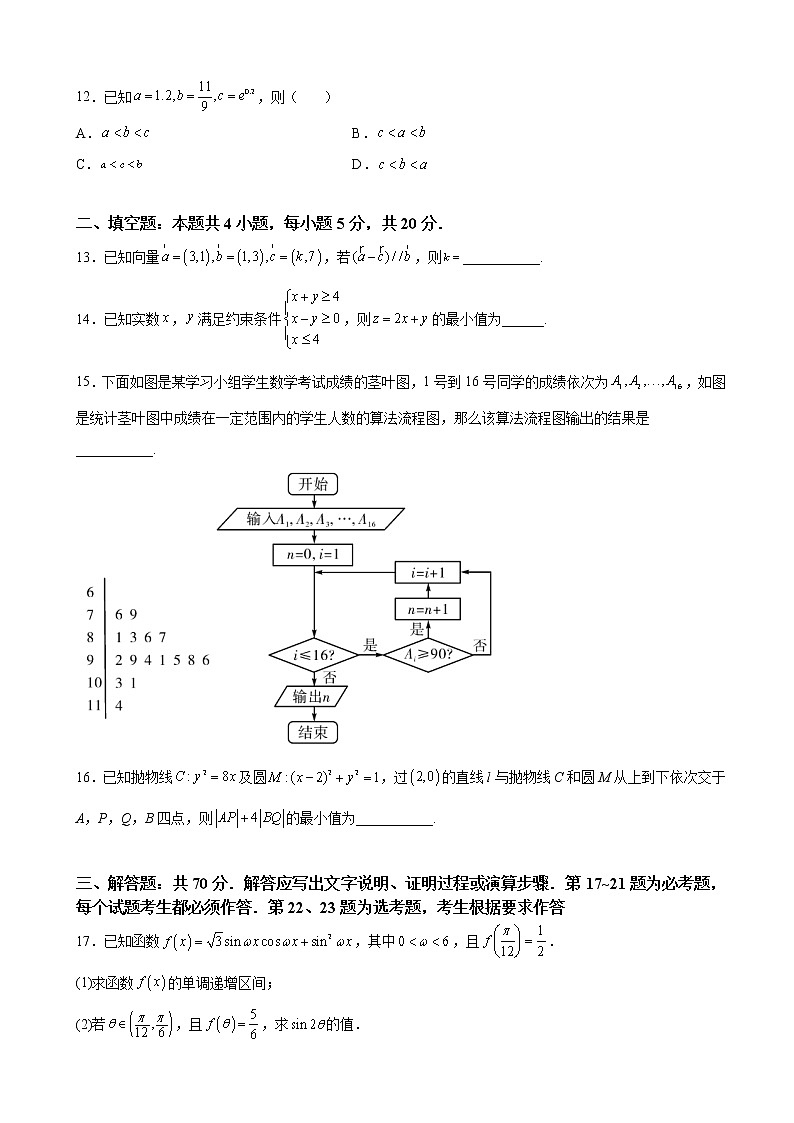
江西师范大学附属中学2022届高三5月三模数学(文)试题一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合,,,则( )A. B. C. D.2.已知是虚数单位,则的虚部是( )A. B. C.1 D.3.已知双曲线的虚轴长为,离心率为,则其方程是( )A. B. C. D.4.把边长为的正方形沿对角线折起,使得平面⊥平面,形成三棱锥的正视图与俯视图如图所示,则侧视图的面积为( )A. B.C. D.5.《张丘建算经》卷上第二十二题为:“今有女善织,日益功疾.初日织五尺,今一月日织九匹三丈.”其意思为今有一女子擅长织布,且从第2天起,每天比前一天多织相同量的布,若第一天织5尺布,现在一个月(按30天计)共织390尺布.则该女子最后一天织布的尺数为( )A.18 B.20 C.21 D.256.已知命题“”的否定是“”;命题在等比数列中,若,则是的充分不必要条件.则下列命题中为真命题的是( )A. B. C. D.7.函数的图象大致为( )A. B.CC. D.8.某种病毒的繁殖速度快、存活时间长.已知a个这种病毒在t天后将达到个,且经过4天后病毒的数量会达到原来的2倍.若再过t天后病毒的数量达到原来的8倍,则( )A.4 B.8 C.12 D.169.地处赣江东岸的腾王阁与岳阳楼、黄鹤楼并称为“江南三大名楼”,是中国古代四大名楼之一、“中国十大历史文化名楼”之一,世称“西江第一楼”.“云销雨霁,彩彻区明.落霞与孤鹜齐飞,秋水共长天一色.渔舟唱晚,响穷彭蠡之滨;雁阵惊寒,声断衡阳之浦”是唐代文学家王勃对腾王阁的生动描写.某位游客(身高忽略不计)从地面D点看楼顶点A的仰角为30°,沿直线前进72米到达E点,此时看点C的仰角为45°,若,则楼高AB约为( )A.58米 B.68米 C.78米 D.88米10.甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩,老师说,你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩,看后甲对大家说:我还是不知道我的成绩,根据以上信息,则( )A.乙可以知道其他两人的成绩 B.丁可以知道四人的成绩C.乙、丁可以知道对方的成绩 D.乙、丁可以知道自己的成绩11.定义在R上的函数满足,且当时,.则函数的所有零点之和为( )A.7 B.14 C.21 D.2812.已知,则( )A. B.C. D. 二、填空题:本题共4小题,每小题5分,共20分.13.已知向量,若,则___________.14.已知实数,满足约束条件,则的最小值为______.15.下面如图是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次为,如图是统计茎叶图中成绩在一定范围内的学生人数的算法流程图,那么该算法流程图输出的结果是___________.16.已知抛物线及圆,过的直线l与抛物线C和圆M从上到下依次交于A,P,Q,B四点,则的最小值为___________. 三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答17.已知函数,其中,且.(1)求函数的单调递增区间;(2)若,且,求的值.18.如图,在四棱锥中,平面,四边形是平行四边形.E、Q分别是的中点,是边长为1的正三角形.(1)证明:;(2)若,求点E到平面的距离.19.随着经济的高速发展,南昌市居住环境及人文环境进一步得到改善.目前已基本依水建成赣江西岸绿道、赣江东岸绿道、乌沙河绿道、玉带河桃花河绿道、抚河故道绿道、幸福渠绿道、艾溪湖瑶湖绿道等城市主干绿道.新建提升20个公园,精心打造100条景观路,织起一张“四横七纵六环”的“绿道网”.另外,位于凤凰洲赣江边的省文化中心的建成已成为展示江西历史文化的地标建筑.省文化中心由省博物馆、省图书馆、省科技馆三馆组成,三个主体建筑由北向南排列,分别隐喻历史、现在与未来,反映出文化发展的路径,描述了探索知识的故事与旅程.作为江西省文化的新地标,城市的新客厅,成为加快推动江西文化强省建设的一个亮丽缩影,成为丰富江西省人民群众精神文化需求的重要阵地.(1)相比老年人而言,青年人更喜欢在闲暇时间选择去省文化中心参观、学习.已知某区青年人的男女比例为3:2,现采用分层抽样的方法从中抽取100名作为样本,对这100位青年是否在闲暇时间去省文化中心进行统计,得条形图如下所示. 男女合计去省文化中心 不去省文化中心 合计 完成下列2×2列联表,并判断是否有90%的把握认为青年人选择去省文化中心与性别有关?(2)现有甲、乙、丙、丁四位青年人,他们每个周末都选择去省文化中心,将他们想去的场馆情况汇总如下:场馆图书馆科技馆博物馆意向甲、乙、丙甲、乙、丁乙、丙、丁 若每人只能从已登记的选择意向中随机选取一个场馆,且每个场馆至多有两人选择,求甲、乙两人选择去同一个场馆的概率.附:0.1000.0500.0250.010,其中.2.7063.8415.0246.635 20.已知函数(e是自然对数的底数,).(1)设的导函数为,试讨论的单调性;(2)当时,若是的极大值点,判断并证明与大小关系.21.已知椭圆的离心率为,点A、B分别是其右顶点和上顶点,坐标原点O到直线AB的距离为.(1)求椭圆C的标准方程;(2)设斜率为的直线l与椭圆的两个交点(自上至下)分别为C、D,问:直线BC与AD的斜率之积是否为定值?若是,求出其大小;若不是,说明理由. (二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.22.[选修4—4:坐标系与参数方程](10分)在直角坐标系中,直线的参数方程为(为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为(1)求曲线的直角坐标方程(2)已知点的直角坐标为,与曲线交于两点,求23.[选修4—5:不等式选讲](10分)已知函数(1)解不等式:(2)记的最小值为,若正实数满足,试求:的最小值
参考答案:1.C【解析】【分析】根据补集的运算求得,再结合并集的运算,即可求解.【详解】由题意,集合,,,根据补集的运算,可得,则.故选:C.2.D【解析】【分析】直接进行复数运算结合虚部的概念即可得结果.【详解】,故其虚部为,故选:D.3.C【解析】【分析】根据题意,得到,结合,求得的值,即可求解.【详解】由题意,双曲线的虚轴长为,离心率为,可得,即,因为,解得:.所以曲线的方程为.故选:C.4.C【解析】【详解】取BD的中点E,连结CE,AE,∵平面ABD⊥平面CBD,∴CE⊥AE,∴三角形直角△CEA是三棱锥的侧视图,∵BD=,∴CE=AE=,∴△CEA的面积S=××=,故选C.5.C【解析】【分析】根据题意,织的布的尺数依次排列形成一个等差数列,其中,结合题设条件列出方程,求得的值,即可求解.【详解】依题意得,织女每天所织的布的尺数依次排列形成一个等差数列,其中,前30项和为390,于是有,解得,即该织女最后一天织21尺布.故选:C.6.B【解析】【分析】根据全称命题的性质、等比数列的性质,结合与、或、非命题的真假原则逐一判断即可.【详解】对于命题p,其否定应该是“”,故p为假命题;对于命题q,依题意.;且;所以“”是“”的充分不必要条件.故q为真命题.由复合命题的真假判断得知为真命题.故选:B7.C【解析】【分析】判断函数的奇偶性,可排除B,D;将特殊值 代入解析式验证,可排除A,由此可得答案.【详解】由,可知为奇函数,排除B,D;又,排除A,故选:C.8.B【解析】【分析】根据题意解指数方程可得参数的值,通过函数值为原来的8倍解出,即可得结果.【详解】由题意得,∴,即.设经过t天后,病毒的数量达到原来的8倍,则有,解得.所以再过天,病毒的数量达到原来的8倍.故选:B.9.A【解析】【分析】设,得到,列出方程,求得的值,即可求得楼高,得到答案.【详解】设,则由题意可得,所以,解得,所以楼高.故选: A.10.D【解析】【分析】根据所给信息进行推理.【详解】甲、乙、丙、丁四位同学中有2位优秀,2位良好,因为甲看乙、丙的成绩后仍不知道自己的成绩,可知乙、丙一人优秀一人良好,则甲、丁一人优秀一人良好,乙看到丙的结果则知道自己的结果,丁看到甲的结果则知道自己的结果,故选:D.11.B【解析】【分析】根据分析得到是周期为4的周期函数,且关于点对称,函数的所有零点之和即为函数与的图像的交点的横坐标之和,画出函数图象,数形结合求出答案.【详解】依题意,是奇函数.又由知,的图像关于对称.,所以是周期为4的周期函数.,所以关于点对称.由于从而函数的所有零点之和即为函数与的图像的交点的横坐标之和.而函数的图像也关于点对称.画出,的图象如图所示.由图可知,共有7个交点,所以函数所有零点和为.故选:B12.C【解析】【分析】构造函数,,利用导数研究函数的单调性,得出,的单调性,得出,令,可得出,再由得出的,令,得出,从而得出结果.【详解】解:先证,令,则,可知在上单调递增,所以,即,令,则,所以;再证即证,令,则,所以在上单调递增,所以,即,令,则,所以,从而.故选:C.13.【解析】【分析】根据平面向量共线的坐标表示列式可解得结果.【详解】,,若,则,解得.故答案为:.14.【解析】【分析】根据约束条件,画出可行域,将目标函数转化为,平移直线,由直线在y轴上截距最小时求解.【详解】由约束条件,画出可行域如图所示阴影部分:将目标函数转化为,平移直线,当直线经过点A时,直线在y轴上截距最小,此时,目标函数取得最小值,由,解得,所以,所以目标函数的最小值为,故答案为:615.10【解析】【分析】根据算法流程图可知是统计大于或等于90分的人数,结合茎叶图即可求解.【详解】由算法流程图可知,其统计的是数学成绩大于或等于90的人数.由茎叶图知,数学成绩大于若等于90的人数为10,因此输出结果为10.故答案为:1016.13【解析】【分析】根据圆心即为抛物线C的焦点F,利用抛物线的定义,结合基本不等式求解.【详解】解:如图所示:圆心即为抛物线C的焦点F.所以,由抛物线的定义,,所以,又易知:,所以,当且仅当,即时等号成立. 所以的最小值为13,故答案为:1317.(1)(2)【解析】【分析】(1)利用二倍角和辅助角公式可化简得,根据可求得,进而得到;令,解不等式即可求得所求的单调递增区间;(2)由可求得,根据同角三角函数关系求得,根据,利用两角和差正弦公式可求得结果.(1),,,解得:,又,,;令,解得:,的单调递增区间为;(2)由(1)知:,;当时,,,.18.(1)证明见解析(2)【解析】【分析】(1)先证得,再由平面证明,进而证得平面,即可证得;(2)由,先设点E到平面的距离为h,求得,再求得,即可求解.(1)由题意知,,,,于是,即,由于,故,又平面,平面,所以,又,平面,可得平面,因为平面,故.(2)由题意得:,设点E到平面的距离为h,因为平面,平面,所以,则,又由(1)知平面,,则平面,则到平面的距离为,而,所以,解得:,即点E到平面的距离为.19.(1)列联表答案见解析,没有90%的把握认为青年人选择去省文化中心与性别有关(2)【解析】【分析】(1)先由分层抽样及条形图完善列联表,再计算,结合临界值作出判断即可;(2)列举出所有的基本事件,从中找出甲、乙两人选择去同一个场馆的基本事件,由古典概型求解即可.(1)由分层抽样知男性共人,女性共人,结合条形图得去省文化中心男性有人,去省文化中心女性人,完成2×2列联表如下: 男女合计去省文化中心402565不去省文化中心201535合计6040100 计算:,所以,没有90%的把握认为青年人选择去省文化中心与性别有关.(2)分两种情况来考虑:4人分别去其中的两个场馆、4人分别去三个场馆.我们将所有的情况列举如下:序号图书馆科技馆博物馆1甲丙乙丁 2乙丙甲丁 3 甲乙丙丁4 甲丁乙丙5甲乙 丙丁6甲丙 乙丁7甲乙丁丙8甲丙乙丁9甲丙丁乙10乙丙甲丁11丙甲乙丁12乙甲丁丙13丙甲丁乙14甲乙丁丙15甲丁乙丙16甲乙丙丁17乙甲丙丁18丙甲乙丁 共有18种选择,其中甲、乙选择同一个场馆的有4种,故概率为.20.(1)答案见解析(2),证明见解析【解析】【分析】(1)求出函数的导数,求出,分为和两种情形,即可得结果;(2)根据(1)中的结论结合极大值的概念,求出满足,求出,结合二次函数的性质可得结果.(1)∵,∴令,则.①若,则,所以单调递增;②若,则当时,,所以所以单调递减;当时,,所以单调递增;综上,当时,在上单调递增;当时在单调递减,在单调递增.(2)由(1)知,当时,在上单调递减,在上单调递增;∵,且故存在两个零点且.的符号及的单调性如下表所示:x+0-0+↗极大↘极小↗ 由于是的一个零点,故,所以于是,∵,∴所以.21.(1);(2)是定值,定值为.【解析】【分析】(1)根据椭圆的离心率的公式,结合点到直线距离公式进行求解即可;(2)把直线l的方程与椭圆的标准方程联立,利用一元二次方程根与系数关系,结合直线斜率的公式进行求解即可.(1)由题意知,,所以,而,所以①,直线AB的方程为,即,所以②,由①②解得:,所以椭圆的标准方程为:;(2)由(1)得椭圆的标准方程为,.直线BC的方程为,与椭圆的方程联立:'化简得解得,即同理,直线AD的方程为.联立化为,∴,解得﹐∴,∴,化为∴∴,为定值.【点睛】关键点睛:利用一元二次方程根与系数关系是解题的关键.22.(1).(2).【解析】【分析】(1)由转化为可化极坐标方程为直角坐标方程;(2)直线参数方程代入曲线的直角坐标方程,应用韦达定理得,利用参数的几何意义求解.【详解】(1)由得,又,所以.即.(2)把直线参数方程方程,得,,由于,所以异号..【点睛】思路点睛:本题考查极坐标方程与直角坐标方程的互化,考查直线的参数方程,在直线与相交问题时,涉及到直线的线段长问题有时用直线的参数方程比较方便,如直线参数方程是(为参数),是直线的倾斜角,,直线与交线交点为,则对应的参数值有:,,如果是直线向上的方向,则为正,否则为负.23.(1);(2).【解析】【分析】(1)由绝对值定义分类讨论;(2)由绝对值三角不等式求得,然后凑配出定值由基本不等式得最小值.【详解】(1)时,不等式为,,所以,时,不等式为恒成立,所以,时,不等式为,,所以,综上不等式的解为,即解集为;(2),当且仅当时等号成立,所以,因为,所以,当且仅当,即时等号成立.的最小值是.【点睛】思路点睛:本题考查解绝对值不等式,求绝对值函数的最值,考查用基本不等式求最值.钥绝对值不等式的一般方法是根据绝对值定义分类讨论去绝对值符号后求解,此时绝对值分段函数可求得函数最值,也可根据绝对值三角不等式求得最值.而用基本不等式求最值需要满足基本不等式的有一个条件:一正二定三相等,特别是相等容易遗漏出错.
相关试卷
这是一份2023届江西师范大学附属中学高三三模考试数学(文)试题含解析,共20页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份2023届江西师范大学附属中学高三三模考试数学(理)试题含解析,共21页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份精品解析:江西师范大学附属中学2023届高三三模考试数学(文)试题(解析版),共23页。试卷主要包含了 已知集合,则, 已知复数满足, 在中,,则, 已知是双曲线C等内容,欢迎下载使用。










