广西专用高考数学一轮复习选修4_4坐标系与参数方程课件新人教A版理

这是一份广西专用高考数学一轮复习选修4_4坐标系与参数方程课件新人教A版理，共46页。PPT课件主要包含了-3-，知识梳理，双基自测，-4-，逆时针，距离OM，xOM，Mρθ，-5-，-6-等内容，欢迎下载使用。

选修4—4　坐标系与参数方程
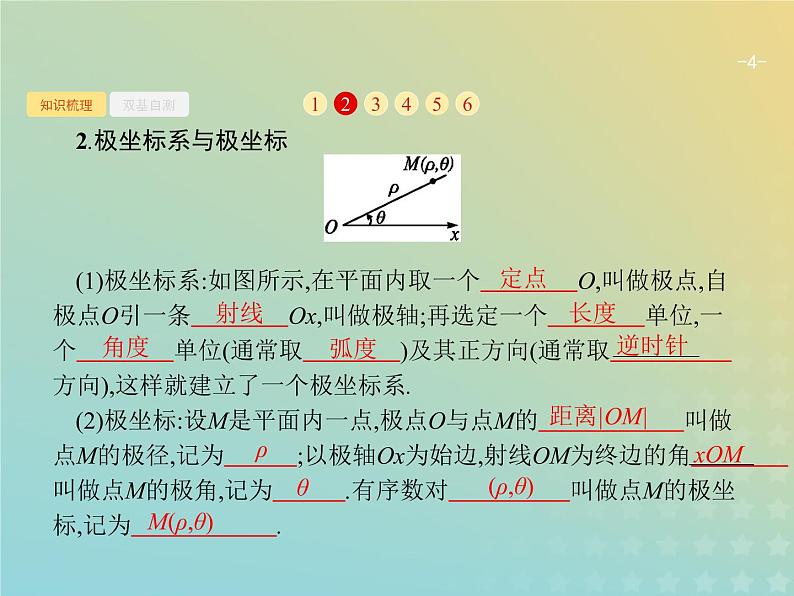
2.极坐标系与极坐标(1)极坐标系:如图所示,在平面内取一个　　　　O,叫做极点,自极点O引一条　　　　Ox,叫做极轴;再选定一个　　　　单位,一个　　　　单位(通常取　　　　)及其正方向(通常取　　　　　方向),这样就建立了一个极坐标系. (2)极坐标:设M是平面内一点,极点O与点M的　　　　　　叫做点M的极径,记为　　　;以极轴Ox为始边,射线OM为终边的角　　　　叫做点M的极角,记为　　　.有序数对　　　　　叫做点M的极坐标,记为　　　　　　. 
3.极坐标与直角坐标的互化(1)设点P的直角坐标为(x,y),它的极坐标为(ρ,θ),(2)把直角坐标转化为极坐标时,通常有不同的表示法(极角相差2π的整数倍).一般取ρ≥0,θ∈[0,2π).
4.直线的极坐标方程(1)若直线过点M(ρ0,θ0),且与极轴所成的角为α,则直线的方程为:ρsin(θ-α)=　　　　　　　　　. (2)几个特殊位置的直线的极坐标方程①直线过极点:θ=θ0和　　　　　　　; ②直线过点M(a,0),且垂直于极轴:　　　　　　; 
ρ0sin(θ0-α)　
5.圆的极坐标方程(1)若圆心为M(ρ0,θ0),半径为r,则圆的方程为　　　　　　　　　 　　　　　　　　　. (2)几个特殊位置的圆的极坐标方程①圆心位于极点,半径为r:ρ=　　　; ②圆心位于M(a,0),半径为a:ρ=　　　　　　　; 
ρ2-2ρ0ρcs(θ-θ0)+ -r2=0　
4.在极坐标系中,直线ρcs θ+ρsin θ=a(a>0)与圆ρ=2cs θ相切,则a=　　　　　. 
考向一　直角坐标方程化为极坐标方程例1以直角坐标系原点O为极点,x轴正方向为极轴建立极坐标系,已知曲线C1的方程为(x-1)2+y2=1,C2的方程为x+y=3,C3是一条经过原点且斜率大于零的直线.(1)求C1与C2的极坐标方程;(2)若C1与C3的一个公共点为A(异于点O),C2与C3的一个公共点为
解:(1)曲线C1的方程为(x-1)2+y2=1,C1的极坐标方程为ρ=2cs θ.
考向二　极坐标方程化为直角坐标方程例2在极坐标系中,曲线C的极坐标方程为 以极点O为直角坐标原点,极轴为x轴的正半轴建立平面直角坐标系.(1)求曲线C的直角坐标方程;(2)设曲线C与x轴、y轴的正半轴分别交于点A,B,P是曲线C上一点,求△ABP面积的最大值.思考如何把极坐标方程化为直角坐标方程?
解题心得1.直角坐标方程化为极坐标方程,只需把公式x=ρcs θ及y=ρsin θ直接代入化简即可.2.极坐标方程化为直角坐标方程要通过变形,构造形如ρcs θ,ρsin θ,ρ2的形式,进行整体代换.其中方程的两边同乘(或同除以)ρ及方程两边平方是常用的变形方法.
对点训练1(1)在平面直角坐标系xOy中,圆C1:(x-3)2+y2=9,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,圆C2的圆心的极坐标为 ,半径为1.①求圆C1的极坐标方程;②设圆C1与圆C2交于A,B两点,求|AB|.
(2)在极坐标系下,已知圆O:ρ=cs θ+sin θ和直线l: 以极点为直角坐标原点,极轴为x轴的正半轴建立平面直角坐标系.①求圆O和直线l的直角坐标方程;②当θ∈(0,π)时,求直线l与圆O公共点的一个极坐标.
解题心得1.参数方程化为普通方程的基本方法就是消参法,常用的消参技巧有代入消元、加减消元、平方后再加减消元等.对于与角θ有关的参数方程,经常用到公式sin2θ+cs2θ=1;在将曲线的参数方程化为普通方程时,还要注意其中的x,y的取值范围,即在消去参数的过程中一定要注意普通方程与参数方程的等价性.2.将普通方程化为参数方程时,只要适当选取参数t,确定x=f(t),再代入普通方程,求得y=g(t),即可化为参数方程 注意参数t的意义和取值范围.直线、圆、圆锥曲线的普通方程有其较为固定的参数方程,只需套用公式即可.
对点训练2在平面直角坐标系xOy中,直线l的参数方程为
(其中t为参数).在以原点O为极点,以x轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=4sin θ.(1)求直线l的普通方程及曲线C的直角坐标方程;(2)设M是曲线C上的一动点,OM的中点为P,求点P到直线l的距离的最小值.
例4在极坐标系中,O为极点,点M(ρ0,θ0)(ρ0>0)在曲线C:ρ=4sin θ上,直线l过点A(4,0)且与OM垂直,垂足为P.
(2)当M在C上运动且P在线段OM上时,求P点轨迹的极坐标方程.思考在极坐标系中,如何求两点之间的距离?
(2)设P(ρ,θ),在Rt△OAP中,|OP|=|OA|cs θ=4cs θ,即ρ=4cs θ.因为P在线段OM上,且AP⊥OM,
解题心得1.在极坐标系中求两点间的距离,可以结合极坐标系刻画点的位置、图形中点的对称等均可求得两点间的距离;也可以利用点的极坐标与直角坐标的互化公式,将点的极坐标转化为直角坐标,然后利用平面直角坐标系中两点间的距离公式求A,B两点间的距离.2.在极坐标系中,经过极点的直线上两点A(ρ1,θ),B(ρ2,θ)的距离|AB|=|ρ2-ρ1|.
对点训练3在平面直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcs θ=4.(1)M为曲线C1上的动点,点P在线段OM上,且满足|OM|·|OP|=16,求点P的轨迹C2的直角坐标方程;
解:(1)设P的极坐标为(ρ,θ)(ρ>0),M的极坐标为(ρ1,θ)(ρ1>0).
由|OM|·|OP|=16得C2的极坐标方程ρ=4cs θ(ρ>0).因此C2的直角坐标方程为(x-2)2+y2=4(x≠0).(2)设点B的极坐标为(ρB,α)(ρB>0).由题设知|OA|=2,ρB=4cs α,于是△OAB面积
例5(2020全国Ⅲ,理22)在直角坐标系xOy中,曲线C的参数方程为 (t为参数,且t≠1),C与坐标轴交于A,B两点.(1)求|AB|;(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求直线AB的极坐标方程.思考如何利用直线的参数方程求直线与曲线相交的弦长?
解:(1)因为t≠1,由2-t-t2=0,得t=-2,所以C与y轴的交点为(0,12);由2-3t+t2=0,得t=2,所以C与x轴的交点为(-4,0).
解题心得求直线与圆锥曲线相交所得的弦长,可以利用直线参数方程中t的几何意义,即弦长=|t1-t2|.
解:(1)圆C的直角坐标方程为(x-1)2+y2=1,即x2+y2-2x=0,化为极坐标方程为ρ2-2ρcs θ=0,即ρ=2cs θ.综上所述,圆C的极坐标方程为ρ=2cs θ.
例6在平面直角坐标系中,已知点A(10,0),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线M的参数方程为 (α∈[0,π]为参数),曲线N的极坐标方程为ρ(1-cs θ)=2.(1)求曲线M的极坐标方程;(2)设曲线M与曲线N的交点为P,Q,求|OP|+|OQ|的值.思考求解参数方程与极坐标方程综合问题的一般思路是什么?
解题心得求解极坐标方程与参数方程综合问题的一般思路:分别化为普通方程和直角坐标方程后求解.转化后可使问题变得更加直观,它体现了化归思想的具体运用.当然,还要结合题目本身特点,确定选择何种方程.
对点训练5在平面直角坐标系中,将曲线C1向左平移2个单位,再将得到的曲线上的每一个点的横坐标保持不变,纵坐标缩短为原来的 ,得到曲线C2,以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,C1的极坐标方程为ρ=4cs α.(1)求曲线C2的参数方程;(2)已知点M在第一象限,四边形MNPQ是曲线C2的内接矩形,求内接矩形MNPQ周长的最大值,并求周长最大时点M的坐标.