

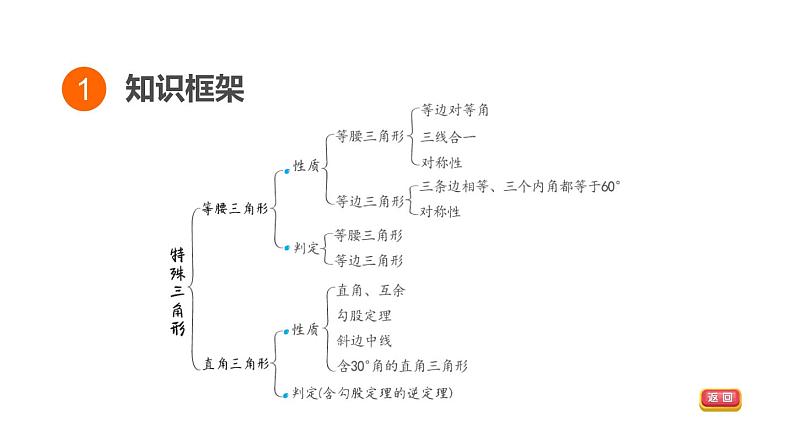





中考数学复习第17课时特殊三角形课堂教学课件
展开· 考点1 等腰三角形的性质(含等边)
· 考点2 等腰三角形的判定(含等边)
· 考点3 直角三角形的性质
· 考点4 直角三角形的判定
考点1 等腰三角形的性质(含等边)
1.等腰三角形的性质:(1)等边对等角:等腰三角形的两个底角相等;(2)三线合一:顶角的平分线、底边上的中线、底边上的高相互重合;(3)等腰三角形是轴对称图形,有1条对称轴.
2.等边三角形的性质:(1)等边三角形的三个内角都相等,并且每一个内角都等于60°;(2)等边三角形是轴对称图形,有3条对称轴.
已知△ABC为等腰三角形.(1)△ABC是________图形,且关于_________________________对称.(2)①若∠BAC=90°,则∠C的度数为________;②若∠BAC=120°,则∠C的度数为________;③若∠BAC=80°,则∠C的度数为________________.
顶角的平分线所在的直线
80°或50°或20°
(3)若△ABC的两边长分别为3和7,则△ABC的周长为____.(4)如图,在△ABC中,AB=AC,AD是∠BAC的平分线.①若BC=12,则BD=________;②当∠B=40°时,∠BAD的度数为________.
(5)若△ABC为等边三角形,AD是BC边上的高.①∠BAD的度数为________;②若BD=3,则△ABC的周长为________.
福建6年中考聚焦[6年2考]
1.【2020福建4分】如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )A.10 B.5 C.4 D.3
2.【2018福建4分】如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )A.15° B.30° C.45° D.60°
3.若实数m、n满足|m-3|+ =0,且m、n恰好是等腰三角形ABC的两条边的边长,则△ABC的周长是( )A.12 B.16 C.12或15 D.15
考点2 等腰三角形的判定(含等边)
1.等腰三角形的判定:(1)有两条边相等的三角形是等腰三角形;(2)等角对等边:如果一个三角形有两个角相等,那么这两个角所对的边也相等.
2.等边三角形的判定:(1)三条边都相等的三角形是等边三角形;(2)三个角都相等的三角形是等边三角形;(3)有一个角是60°的等腰三角形是等边三角形.
1.【2022龙岩质检4分】如图,△ABC中,AD平分∠BAC,E是BC的中点,AD⊥BD,AC=7,AB=3,则DE的值为( )
2.【2021厦门二模4分】如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,BD平分∠ABC,AD∥BC,则AD的长是________.
3.在平面直角坐标系中,O为坐标原点,已知点A(2,-1),在x轴上确定一点P,使得△AOP为等腰三角形,则符合条件的点P有________个.
考点3 直角三角形的性质
1.两锐角之和等于90°.2.斜边上的中线等于斜边的一半.3.30°角所对的直角边等于斜边的一半.4.勾股定理:如果直角三角形的两条直角边分别为a,b,斜边为c,那么a2+b2=c2.
*5.在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.(小题可直接用,大题需先证明)
如图,已知三角形ABC为直角三角形,∠BAC=90°,AD为BC边上的高,AE为BC边上的中线.(1)若∠B=50°,则∠C=________;(2)若BC=2 ,AB= ,则S△ABC=________,AD=________;(3)若BC=4,∠C=30°,则BD=________;
(4)若∠ABD=45°,AB=2 ,则△ABC的形状为________________,CD=________;(5)若BD=2,AE=10,则AD=________;(6)若F,G分别是AB,AC的中点,FG+AE=8,则BE=________.
1.【2018福建4分】如图,Rt△ABC中,∠ACB=90°,AB=6,D是AB的中点,则CD=________.
2.【2018福建4分】把两个同样大小的含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A,且另三个锐角顶点B,C,D在同一直线上.若AB= ,则CD=________.
3.【2022厦门质检4分】在△ABC中,∠C=90°,AB=10,AC=8,则BC的长为________.
4.如图,数字代表所在正方形的面积,则A所代表的正方形的面积为________.
5.【2022福建模拟4分】如图,在Rt△ABC中,∠C=90°,点D在线段BC上,且∠B=30°,∠ADC=60°,BC=3 ,则BD的长度为________.
考点4 直角三角形的判定
1.有一个角为90°的三角形是直角三角形.2.勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2 ,那么这个三角形是直角三角形.3.有两个角互余的三角形是直角三角形.*4.一条边的中线等于这条边的一半的三角形是直角三角形.(小题可直接用,大题需先证明)
1.已知,在△ABC中,∠B=50°,当∠A=__________时,△ABC为直角三角形.
2.【2021厦门二模4分】三个顶点都在网格点上,且有一个角为直角的三角形称为网格直角三角形.如图,在8×8的网格中,若△ABC为网格直角三角形,则满足条件的C点个数为( )A.6 B.7 C.13 D.15
3.点A(2,m),B(2,m-5)在平面直角坐标系中,点O为坐标原点.若△ABO是直角三角形,则m的值不可能是( )A.4 B.2 C.1 D.0
1.【2022宿迁】若等腰三角形的两边长分别是3 cm和5 cm,则这个等腰三角形的周长是( )A.8 cmB.13 cmC.8 cm或13 cmD.11 cm或13 cm
2.△ABC中,AB=4,∠B=∠C=15°,则△ABC的面积是( )A.2 B.4 C.6 D.8
3.下列对△ABC的判断,错误的是( )A.若AB=AC,∠B=60°,则△ABC是等边三角形B.若∠A∶∠B∶∠C=2∶3∶5,则△ABC是直角三角形C.若∠A=20°,∠B=80°,则△ABC是等腰三角形D.若AB=BC,∠C=40°,则∠B=40°
4.【2022滨州】如图,屋顶钢架外框是等腰三角形,其中AB=AC,立柱AD⊥BC,且顶角∠BAC=120°,则∠C的大小为________.
5.【2022云南】已知△ABC是等腰三角形.若∠A=40°,则△ABC的顶角度数是______________.
6.已知在△ABC中,∠C=90°,AC=6,BC=8,点D是BC边上的动点,P是AB边的中点,若要使△BPD为直角三角形,则BD=___________.
7.如图,△ABC中,∠C=90°,CA=8 cm,CB=6 cm,D为动点,沿着C→A→B→C的路径运动(再次到达C点则停止运动),点D的运动速度为2 cm/s,设点D的运动时间为t s.(1)当点D在AC上运动时,若DC=BC,则t=________;
(2)若点D与△ABC某一顶点的连线平分△ABC的周长,求t的值.
2023中考复习大串讲初中数学第17课时特殊三角形 课件(福建版): 这是一份2023中考复习大串讲初中数学第17课时特殊三角形 课件(福建版),共41页。PPT课件主要包含了要点知识,题串考点,轴对称,第二空答案不唯一,福建6年中考聚焦,等腰直角三角形,°或90°,°或100°等内容,欢迎下载使用。
中考数学复习第17课时特殊三角形课后练课件: 这是一份中考数学复习第17课时特殊三角形课后练课件,共19页。PPT课件主要包含了基础题,∠A=60°,答案不唯一,综合应用创新题等内容,欢迎下载使用。
中考数学复习第23课时菱形课堂教学课件: 这是一份中考数学复习第23课时菱形课堂教学课件,共16页。PPT课件主要包含了题串考点,福建6年中考聚焦等内容,欢迎下载使用。












