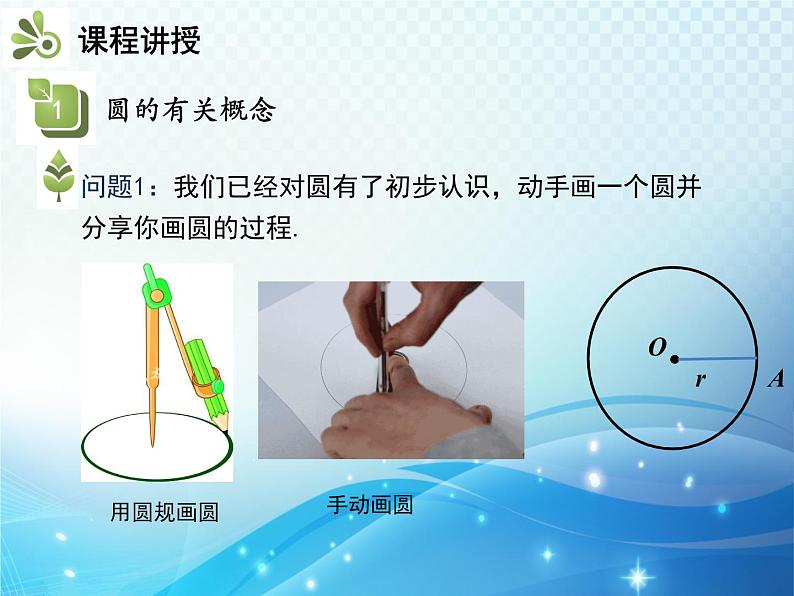
2020-2021学年24.2.1 点与圆的位置关系以及圆的有关概念教学ppt课件

这是一份2020-2021学年24.2.1 点与圆的位置关系以及圆的有关概念教学ppt课件，共25页。PPT课件主要包含了知识要点，圆的有关概念，点和圆的位置关系，圆的对称性，用圆规画圆，手动画圆，ACAB，OBr，OCr，①②③④等内容，欢迎下载使用。

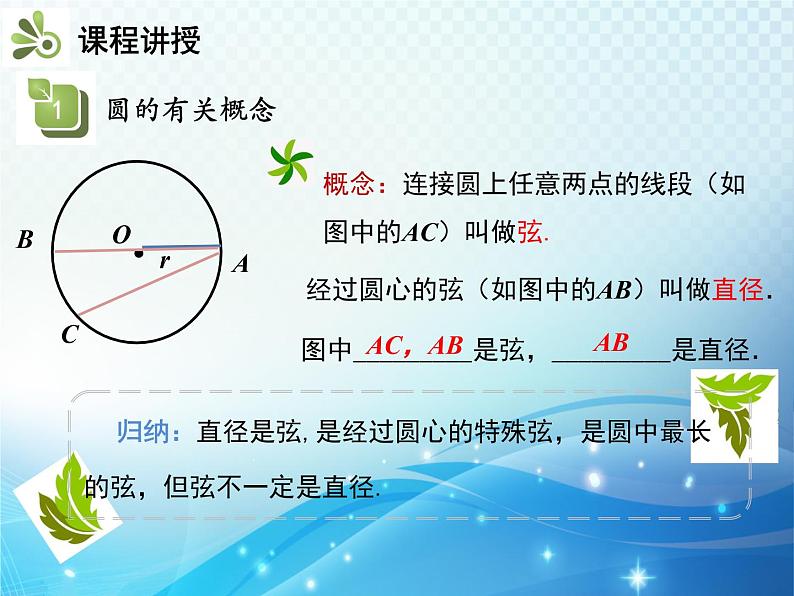
经过圆心的弦（如图中的AB）叫做直径．
图中_________是弦，_________是直径．
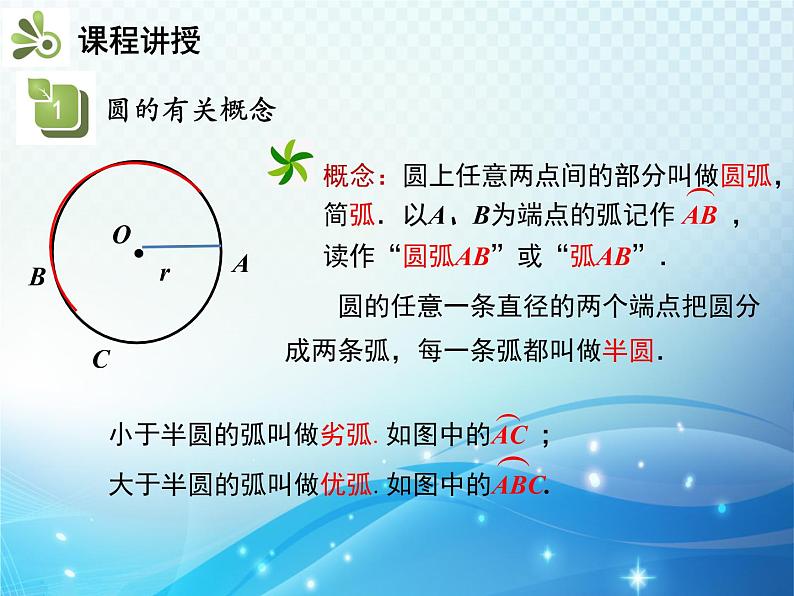
圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆．
击中靶上不同位置的成绩是根据距离靶心的距离决定的，距离靶心越近，得分越高.
要进一步解决这个问题，我们需要研究点和圆的位置关系.
我们知道，圆上所有的点到圆心的距离都等于半径.
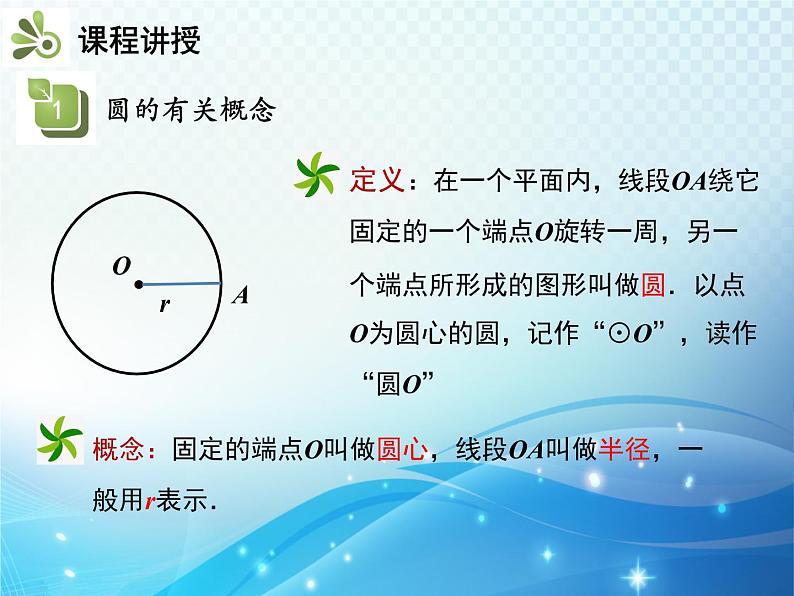
如图，设⊙O的半径为r，点A在圆内，点B在圆上，点C在圆外.
容易看出：OA____r
反过来说：如果OAOB=r，点B在圆____
OC>r，点C在圆_____
1.下列条件能确定圆的是（ ）A.以点O为圆心B.以2 cm为半径C.以点O为圆心，以3 cm为半径D.经过已知点A2.过圆上一点可以作出圆的最长弦的条数为（ ） A.1条 B.2条 C.3条 D.无数条
3.如图，王大伯家屋后有一块长为12 m、宽8 m的矩形空地，他在以长边BC为直径的半圆内种菜，他家养的一只羊平时拴在A处的一棵树上，为了不让羊吃到菜，拴羊的绳长可以为（ ） A.3 m B.5 m C.7 m D.9 m
4.下面3个命题：①半径相等的两个圆是等圆；②长度相等的弧是等弧；③一条弦把圆分成两条弧，这两条弧不可能是等弧.其中真命题的个数为（ ） A.0个 B.1个 C.2个 D.3个
5.已知⊙A的半径为5，圆心A的坐标为（1，0），点P的坐标为（-2，4），则点P与⊙A的位置关系是（ ） A.点P在⊙A上 B.点P在⊙A内 C.点P在⊙A外 D.不能确定
6.如图，AB是⊙O的直径，∠BAC=42°,点D是弦AC的中点，则∠DOC的度数是_______度.
8.如图，CD是⊙O的直径，∠EOD=78°,AE交⊙O于点B，且AB=OC，求∠A的度数.
∵AB=OC,OB=OC,
∴AB=OB,∴∠BOC=∠A.
∴∠E=∠OBE=∠BOC+∠A=2∠A，
∴∠DOE=∠E+∠A=3∠A，
9.如图，在△ABC中，BD，CE是两条高，点O为BC的中点，连接OD，OE.求证：B，C，D，E四个点在以点O为圆心的同一个圆上.
∴B，C，D，E四个点在以点O为圆心的同一个圆上.
证明 ∵BD，CE是两条高，
∴∠BDC=∠BEC=90°.
∴OB=OC=OD=OE.