
第19讲 统计与概率 2023年中考数学一轮复习专题训练(江苏专用)
展开第19讲 统计与概率 2023年中考数学一轮复习专题训练(江苏专用)
一、单选题
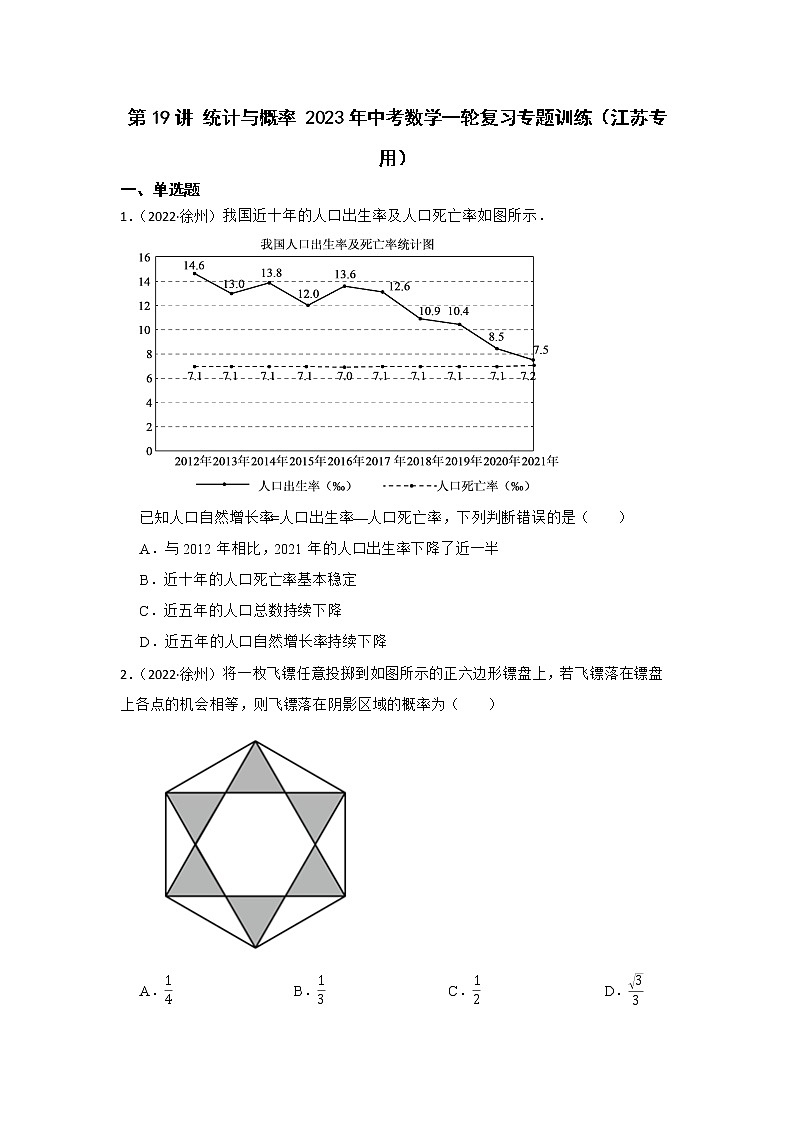
1.(2022·徐州)我国近十年的人口出生率及人口死亡率如图所示.
已知人口自然增长率=人口出生率—人口死亡率,下列判断错误的是( )
A.与2012年相比,2021年的人口出生率下降了近一半
B.近十年的人口死亡率基本稳定
C.近五年的人口总数持续下降
D.近五年的人口自然增长率持续下降
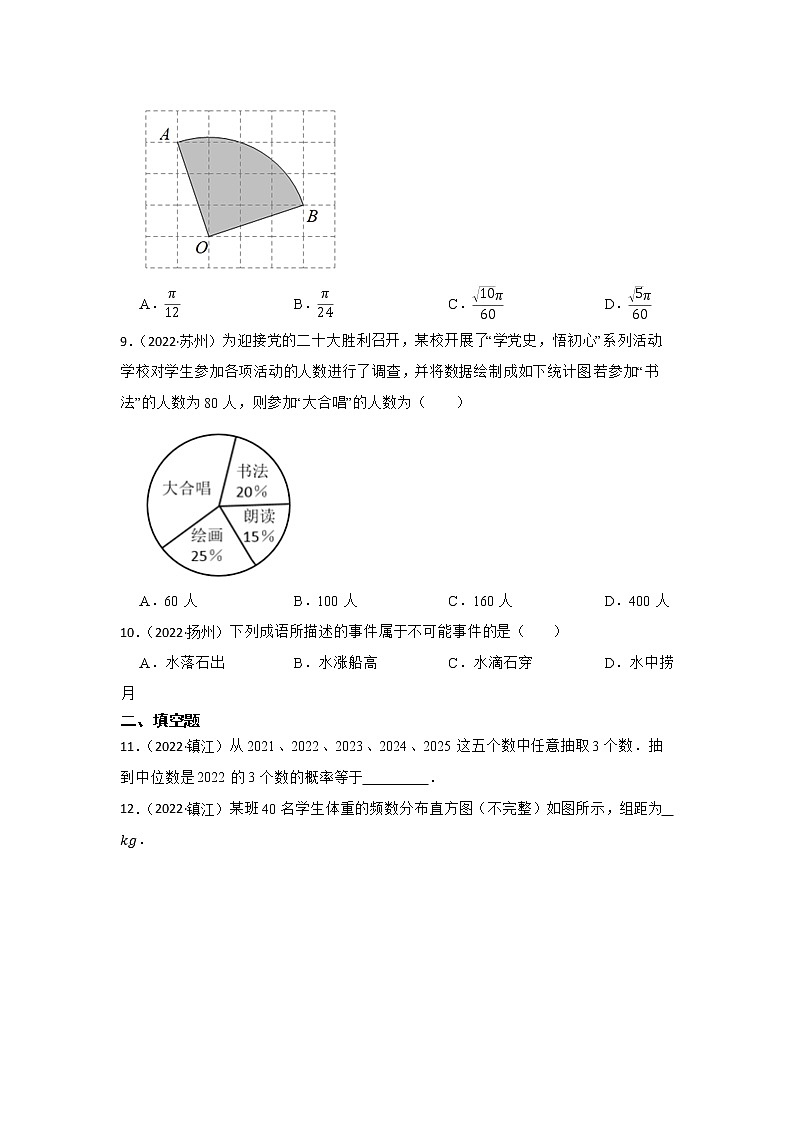
2.(2022·徐州)将一枚飞镖任意投掷到如图所示的正六边形镖盘上,若飞镖落在镖盘上各点的机会相等,则飞镖落在阴影区域的概率为( )
A.14 B.13 C.12 D.33
3.(2022·镇江)第1组数据为:0、0、0、1、1、1,第2组数据为:0,0,⋯,0︷m个0、1,1,⋯,1︷n个1,其中m、n是正整数.下列结论:①当m=n时,两组数据的平均数相等;②当m>n时,第1组数据的平均数小于第2组数据的平均数;③当m
4.(2022·盐城)一组数据-2,0,3,1,-1的极差是( )
A.2 B.3 C.4 D.5
5.(2022·泰州)如图,一张圆桌共有3个座位,甲、乙,丙3人随机坐到这3个座位上,则甲和乙相邻的概率为( )
A.13 B.12 C.23 D.1
6.(2022·无锡)已知一组数据:111,113,115,115,116,这组数据的平均数和众数分别是( )
A.114,115 B.114,114 C.115,114 D.115,115
7.(2022·泗洪模拟)某市四月份连续7天的最高气温依次是:18,15,16,15,16,18,19单位(℃),则这组数据的中位数是( )
A.16℃ B.17℃ C.18℃ D.19℃
8.(2022·苏州)如图,在 5×6 的长方形网格飞镖游戏板中,每块小正方形除颜色外都相同,小正方形的顶点称为格点,扇形OAB的圆心及弧的两端均为格点.假设飞镖击中每一块小正方形是等可能的(击中扇形的边界或没有击中游戏板,则重投1次),任意投掷飞镖1次,飞镖击中扇形OAB(阴影部分)的概率是( )
A.π12 B.π24 C.10π60 D.5π60
9.(2022·苏州)为迎接党的二十大胜利召开,某校开展了“学党史,悟初心”系列活动.学校对学生参加各项活动的人数进行了调查,并将数据绘制成如下统计图.若参加“书法”的人数为80人,则参加“大合唱”的人数为( )
A.60人 B.100人 C.160人 D.400人
10.(2022·扬州)下列成语所描述的事件属于不可能事件的是( )
A.水落石出 B.水涨船高 C.水滴石穿 D.水中捞月
二、填空题
11.(2022·镇江)从2021、2022、2023、2024、2025这五个数中任意抽取3个数.抽到中位数是2022的3个数的概率等于 .
12.(2022·镇江)某班40名学生体重的频数分布直方图(不完整)如图所示,组距为 kg.
13.(2022·南通)为了了解“双减”背景下全国中小学生完成课后作业的时间情况,比较适合的调查方式是 (填“全面调查”或“抽样调查”).
14.(2022·盐城)如图所示,电路图上有A,B,C三个开关和一个小灯泡,闭合开关C或者同时闭合开关A,B,都可使小灯泡发光.现任意闭合其中一个开关,则小灯泡发光的概率等于
15.(2022·泰州)学校要从王静,李玉两同学中选拔一人参加运动会志愿者工作,选拔项目为普通话,体育知识和旅游知识.并将成绩依次按4∶3∶3计分. 两人的各项选拔成绩如右表所示,则最终胜出的同学是 .
普通话
体育知识
旅游知识
王静
80
90
70
李玉
90
80
70
16.(2022·泗洪模拟)如图,从一个大正方形中截去面积为3cm2和12cm2的两个小正方形,若随机向大正方形内投一粒米,则米粒落在图中阴影部分的概率为 .
17.(2022·扬州)某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如图所示,甲、乙两选手成绩的方差分别记为S甲2、S乙2,则S甲2 S乙2.(填“>”“<”或“=”)
18.(2022·宿迁)已知一组数据:4,5,5,6,5,4,7,8,则这组数据的众数是 .
19.(2022·海陵模拟).一个口袋中装有2个红球、1个白球,现小明和小丽用两种不同的方法从袋中随机摸球.小明从袋中一次性随机摸取2个球,都是红球的概率记为P1;小丽先从袋中随机摸出1个球,记下颜色后放回,再从袋中随机摸出1个球,两次都是红球的概率记为P2.则P1与P2的大小关系是P1 P2(填“>”、“<”或“=”).
20.(2022·沭阳模拟)甲、乙两位同学在近五次数学测试中,平均成绩均为85分,方差分别为S甲2=0.70、S乙2=1.82,甲、乙两位同学成绩较稳定的是 同学.
三、综合题
21.(2022·徐州)如图,将下列3张扑克牌洗匀后数字朝下放在桌面上.
(1)从中随机抽取1张,抽得扑克牌上的数字为3的概率为 ;
(2)从中随机抽取2张,用列表或画树状图的方法,求抽得2张扑克牌的数字不同的概率.
22.(2022·徐州)如图,下列装在相同的透明密封盒内的古钱币,其密封盒上分别标有古钱币的尺寸及质量,例如:钱币“文星高照”密封盒上所标“45.4*2.8mm,24.4g”是指该枚古钱币的直径为45.4mm,厚度为2.8mm,质量为24.4g.已知这些古钱币的材质相同.
根据图中信息,解决下列问题.
(1)这5枚古钱币,所标直径的平均数是 mm,所标厚度的众数是 mm,所标质量的中位数是 g;
(2)由于古钱币无法从密封盒内取出,为判断密封盒上所标古钱币的质量是否有错,桐桐用电子秤测得每枚古钱币与其密封盒的总质量如下:
名称
文星高照
状元及第
鹿鹤同春
顺风大吉
连中三元
总质量/g
58.7
58.1
55.2
54.3
55.8
请你应用所学的统计知识,判断哪枚古钱币所标的质量与实际质量差异较大,并计算该枚古钱币的实际质量约为多少克.
23.(2022·镇江)一只不透明的袋子中装有2个白球、1个红球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出一个球,摸到红球的概率等于 ;
(2)搅匀后从中任意摸出一个球,记录颜色后放回、搅匀,再从中任意摸出一个球.用列表或画树状图的方法,求2次都摸到红球的概率.
24.(2022·镇江)某地交警在一个路口对某个时段来往的车辆的车速进行监测,统计数据如下表:
车速(km/h)
40
41
42
43
44
45
频数
6
8
15
a
3
2
其中车速为40、43(单位:km/h)的车辆数分别占监测的车辆总数的12%、32%.
(1)求出表格中a的值;
(2)如果一辆汽车行驶的车速不超过40km/h的10%,就认定这辆车是安全行驶.若一年内在该时段通过此路口的车辆有20000辆,试估计其中安全行驶的车辆数.
25.(2022·南通)不透明的袋子中装有红球、黄球、蓝球各一个,这些球除颜色外无其他差别.
(1)从袋子中随机摸出一个球,摸到蓝球的概率是 ;
(2)从袋子中随机摸出一个球后,放回并摇匀,再随机摸出一个球.求两次摸到的球的颜色为“一红一黄”的概率.
26.(2022·南通)为了了解八年级学生本学期参加社会实践活动的天数情况,A,B两个县区分别随机抽查了200名八年级学生.根据调查结果绘制了统计图表,部分图表如下:
A,B两个县区的统计表
平均数
众数
中位数
A县区
3.85
3
3
B县区
3.85
4
2.5
(1)若A县区八年级共有约5000名学生,估计该县区八年级学生参加社会实践活动不少于3天的学生约为 名;
(2)请对A,B两个县区八年级学生参加社会实践活动的天数情况进行比较,做出判断,并说明理由.
27.(2022·盐城)合理的膳食可以保证青少年体格和智力的正常发育.综合实践小组为了解某校学生膳食营养状况,从该校1380名学生中调查了100名学生的膳食情况,调查数据整理如下:
中国营养学会推荐的三大营养素供能比参考值
蛋白质
10%~15%
脂肪
20%~30%
碳水化合物
50%~65%
注:供能比为某物质提供的能量占人体所需总能量的百分比.
(1)本次调查采用 的调查方法;(填“普查”或“抽样调查”)
(2)通过对调查数据的计算,样本中的蛋白质平均供能比约为14.6%,请计算样本中的脂肪平均供能比和碳水化合物平均供能比;
(3)结合以上的调查和计算,对照下表中的参考值,请你针对该校学生膳食状况存在的问题提一条建议.
28.(2022·常州)为减少传统塑料袋对生态环境的破坏,国家提倡使用可以在自然环境下(特定微生物、温度、湿度)较快完成降解的环保塑料袋.调查小组就某小区每户家庭1周内环保塑料袋的使用情况进行了抽样调查,使用情况为A(不使用)、B(1~3个)、C(4~6个)、D(7个及以上),以下是根据调查结果绘制的统计图的一部分.
(1)本次调查的样本容量是 ,请补全条形统计图;
(2)已知该小区有1500户家庭,调查小组估计:该小区1周内使用7个及以上环保塑料袋的家庭约有225户.调查小组的估计是否合理?请说明理由.
29.(2022·常州)在5张相同的小纸条上,分别写有语句:①函数表达式为y=x;②函数表达式为y=x2;③函数的图象关于原点对称;④函数的图象关于y轴对称;⑤函数值y随自变量x增大而增大.将这5张小纸条做成5支签,①、②放在不透明的盒子A中搅匀,③、④、⑤放在不透明的盒子B中搅匀.
(1)从盒子A中任意抽出1支签,抽到①的概率是 ;
(2)先从盒子A中任意抽出1支签,再从盒子B中任意抽出1支签.求抽到的2张小纸条上的语句对函数的描述相符合的概率.
30.(2022·泰州)农业、工业和服务业统称为“三产”,2021年泰州市“三产”总值增长率在全省排名第一.观察下列两幅统计图,回答问题.
(1)2017—2021年农业产值增长率的中位数是 %﹔若2019年“三产”总值为5200亿元,则2020年服务业产值比2019年约增加 亿元(结果保留整数).
(2)小亮观察折线统计图后认为:这五年中,每年服务业产值都比工业产值高,你同意他的说法吗?请结合扇形统计图说明你的理由.
答案解析部分
1.【答案】C
【解析】【解答】解:A、 与2012年相比,2021年的人口出生率下降了近一半,故该选项正确,不符合题意;
B、 近十年的人口死亡率基本稳定,故该选项正确,不符合题意;
C、近五年的人口总数持续上升,只是自然增长率在变小,故该选项不正确,符合题意;
D、近五年的人口自然增长率持续下降,故该选项正确,不符合题意.
故答案为:C.
【分析】根据折线统计图可得2012年的人口出生率为14.6,2021年的人口出生率为7.5,据此判断A;根据人口死亡率图可判断B;根据人口出生率统计图可判断C、D.
2.【答案】B
【解析】【解答】解:如图,
根据题意得:图中每个小三角形的面积都相等,
设每个小三角形的面积为a,则阴影的面积为6a,正六边形的面积为18a,
∴将一枚飞镖任意投掷到镖盘上,飞镖落在阴影区域的概率为6a18a=13.
故答案为:B.
【分析】根据题意得:图中每个小三角形的面积都相等,设每个小三角形的面积为a,则阴影的面积为6a,正六边形的面积为18a,然后根据几何概率公式进行计算.
3.【答案】B
【解析】【解答】解:①第1组数据的平均数为: 0+0+0+1+1+16=0.5 ,
当m=n时,第2组数据的平均数为: 0×m+1×nm+n=m2m=0.5 ,
故①正确;
②第1组数据的平均数为: 0+0+0+1+1+16=0.5 ,
当 m>n 时,m+n>2n,则第2组数据的平均数为: 0×m+1×nm+n=nm+n
故②错误;
③第1组数据的中位数是 0+12=0.5 ,
当 m
④第1组数据的方差为 (0-0.5)2×3+(1-0.5)2×36=0.25 ,
当 m=n 时,第2组数据的方差为 (0-0.5)2×m+(1-0.5)2×nm+n ,
=0.25m+0.25m2m
=0.25 ,
∴当 m=n 时,第2组数据的方差等于第1组数据的方差.
故④错误,
综上所述,其中正确的是①③;
故答案为:B.
【分析】①数据的总和除以数据的总个数等于这组数据的平均数,据此求出第1组、第2组平均数进行比较;②求出m>n时,第2组数据的平均数进行比较;③中位数:将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数 叫做这组数据的中位数;据此求出1组数据的中位数,当m<n时,若m+n为奇数,m+n为偶数,分情况讨论求出第2组数据的中位数进行比较;④方差就是一组数据的各个数据与平均数差的平方和的平均数,据此求出第1组、第2组方差进行比较.
4.【答案】D
【解析】【解答】解:∵这组数据中最大的为3,最小的为-2
∴极差为最大值3与最小值-2的差为:3-(-2)=3+2=5.
故答案为:D.
【分析】由题意可得这组数据中最大的为3,最小的为-2,利用最大值减去最小值可得极差.
5.【答案】D
【解析】【解答】解:这张圆桌的3个座位是彼此相邻的,甲乙相邻是必然事件,所以甲和乙相邻的概率为1.
故答案为:D.
【分析】由图形可得:甲乙相邻是必然事件,据此可得甲和乙相邻的概率.
6.【答案】A
【解析】【解答】解:这组数据的平均数为:(1+3+5+5+6)÷5+110=114,
115出现了2次,出现次数最多,则众数为:115.
故答案为:A.
【分析】首先以110为基准,求出各个数据与基准数的差之和,然后除以数据的个数,再加上基准数可得这组数据的平均数;找出出现次数最多的数据可得众数.
7.【答案】A
【解析】【解答】解:把这组数据按照从小到大的顺序排列为:15,15,16,16,18,18,19,
所以最中间的那个数为第四个数,其数值是16
即这组数据的中位数为16
故答案为:A.
【分析】把这组数据按照从小到大的顺序进行排列,找出最中间的数据即为中位数.
8.【答案】A
【解析】【解答】解:由图可知,总面积为:5×6=30, OB=32+12=10 ,
∴阴影部分面积为: 90·π×10360=5π2 ,
∴飞镖击中扇形OAB(阴影部分)的概率是 5π230=π12 .
故答案为:A.
【分析】首先求出长方形网格的面积,利用勾股定理求出OB,结合扇形的面积公式求出阴影部分的面积,然后用扇形的面积除以整个矩形的面积进行计算.
9.【答案】C
【解析】【解答】解:总人数为 80÷20%=400 .
则参加“大合唱”的人数为 400×(1-25%-15%-20%)=160 人.
故答案为:C.
【分析】利用参加“书法”的人数除以所占的比例可得总人数,根据百分比之和为1求出参加“大合唱”的人数所占的比例,然后乘以总人数可得对应的人数.
10.【答案】D
【解析】【解答】解:A、水落石出是必然事件,不符合题意;
B、水涨船高是必然事件,不符合题意;
C、水滴石穿是必然事件,不符合题意;
D、水中捞月是不可能事件,符合题意.
故答案为:D.
【分析】必然事件:在一定条件下,一定会发生的事件,叫做必然事件,简称必然事件;不可能事件:在一定条件下,一定不可能发生的事件,叫做不可能事件,简称不可能事件;随机事件:随机事件是在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件,据此一一判断得出答案.
11.【答案】310
【解析】【解答】解:根据题意,画树状图如图,
2022为中位数的情形有6种,
2022为中位数的情形有6种,
2022为中位数的情形有2种,
2022为中位数的情形有2种,
2022为中位数的情形有2种,
共有60种情况,其中抽到中位数是2022的3个数的情况有18种,
则抽到中位数是2022的3个数的概率等于 1860=310 ,
故答案为: 310.
【分析】画出树状图,找出抽到中位数是2022的3个数的情况数,然后根据概率公式进行计算.
12.【答案】5
【解析】【解答】解:依题意,组距为 (69.5-39.5)÷6=5 kg.
故答案为:5.
【分析】首先利用最大值减去最小值求出极差,然后除以组数可得组距.
13.【答案】抽样调查
【解析】【解答】解:为了了解“双减”背景下全国中小学生完成课后作业的时间情况,比较适合的调查方式是抽样调查.
故答案为:抽样调查.
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似,据此可得答案.
14.【答案】13
【解析】【解答】解:根据题意,三个开关,只有闭合C小灯泡才发光,所以小灯泡发光的概率等于13.
故答案为:13.
【分析】根据题意可得:三个开关,只有闭合C小灯泡才发光,然后根据概率公式进行计算.
15.【答案】李玉
【解析】【解答】解:王静得分:80×4+90×3+70×34+3+3=80(分)
李玉得分:90×4+80×3+70×34+3+3=81(分)
∵81分>80分,
∴最终胜出的同学是李玉.
故答案为:李玉.
【分析】利用普通话得分×权重+体育知识得分×权重+旅游知识得分×权重的和除以权重的和,分别求出王静、李玉的得分,然后进行比较即可判断.
16.【答案】49
【解析】【解答】解:∵两个空白正方形的面积分别为12和3,
∴边长分别为23和3,
∴大正方形的边长为23+3=33,
∴大正方形的面积为(33)2=27,
∴阴影部分的面积为27-12-3=12,
∴米粒落在图中阴影部分的概率=1227=49.
故答案为:49.
【分析】根据空白正方形的面积可得边长分别为23和3,则大正方形的边长为33,求出大正方形的面积,然后求出阴影部分的面积,接下来根据几何概率公式进行计算即可.
17.【答案】>
【解析】【解答】解:根据折线统计图中数据,
x甲=(5+10+9+3+8)÷5=7,x乙=(8+6+8+6+7)÷5=7,
∴s甲2=15×[(5-7)2+(10-7)2+(9-7)2+(3-7)2+(8-7)2]=6.8,
s乙2=15×[(8-7)2+(6-7)2+(8-7)2+(6-7)2+(7-7)2]=0.8,
∴s甲2>s乙2
故答案为:>.
【分析】根据折线统计图可得甲、乙选手五次射击的成绩,利用平均数的计算公式分别求出甲、乙的平均数,然后结合方差的计算公式求出方差,最后比较即可.
18.【答案】5
【解析】【解答】解:这组数据中5出现3次,次数最多,
所以这组数据的众数是5.
故答案为:5.
【分析】找出出现次数最多的数据即为众数.
19.【答案】<
【解析】【解答】解:小明从袋中一次性随机摸取2个球,所有等可能结果如下表所示:
红
红
白
红
(红,红)
(白,红)
红
(红,红)
(白,红)
白
(红,白)
(红,白)
由表知,共有6种等可能结果,其中都是红球的有2种结果,
所以都是红球的概率P1=26=13;
小丽先从袋中随机摸出1个球,记下颜色后放回,再从袋中随机摸出1个球,所有等可能结果如下表所示:
红
红
白
红
(红,红)
(红,红)
(白,红)
红
(红,红)
(红,红)
(白,红)
白
(红,白)
(红,白)
(白,白)
由表知,共有9种等可能结果,其中两次都是红球的有4种结果,
所以两次都是红球的概率P2=49;
∴P1<P2,
故答案为:<.
【分析】先列表,再求出概率,最后比较大小即可。
20.【答案】甲
【解析】【解答】解:∵S甲2
故答案为:甲.
【分析】方差用来衡量一批数据的波动大小的,在样本容量相同积的情况下,方差越大,说明数据的波动越大,越不稳定,方差越小,说明数据的波动越小,越稳定,据此判断.
21.【答案】(1)23
(2)解:画树状图如下:
如图,共有6种等可能的结果,其中抽到2张扑克牌的数字不同的结果有4种,
∴抽得2张扑克牌的数字不同的概率为P=46=23.
【解析】【解答】解:(1)根据题意,3张扑克牌中,数字为2的扑克牌有一张,数字为3的扑克牌有两张,
∴从中随机抽取1张,抽得扑克牌上的数字为3的概率为23.
故答案为:23;
【分析】(1)共有3张扑克牌,从中任取一张,能抽到数字3的有两种等可能的情况,从而利用概率公式即可算出答案;
(2)此题是抽取吧放回类型,画出树状图,找出总情况数以及抽到2张扑克牌的数字不同的情况数,然后根据概率公式进行计算.
22.【答案】(1)45.74;2.3;21.7
(2)解:
名称
文星高照
状元及第
鹿鹤同春
顺风大吉
连中三元
总质量/g
58.7
58.1
55.2
54.3
55.8
盒标质量
24.4
24.0
13.0
20.0
21.7
盒子质量
34.3
34.1
42.2
34.3
34.1
∴“鹿鹤同春”密封盒的质量异常,故“鹿鹤同春”所标质量与实际质量差异较大.
其余四个盒子质量的平均数为:34.3+34.1+34.3+34.14=34.2g,
55.2-34.2=21.0g
故“鹿鹤同春”的实际质量约为21.0克.
【解析】【解答】解:(1)平均数:15×(45.4+48.1+45.1+44.6+45.5)=45.74mm;
这5枚古钱币的厚度分别为:2.8mm,2.4mm,2.3mm,2.1mm,2.3mm,
其中2.3mm出现了2次,出现的次数最多,
∴这5枚古钱币的厚度的众数为2.3mm;
将这5枚古钱币的重量按从小到大的顺序排列为:13.0g,20.0g,21.7g,24.0g,24.4g,
∴这5枚古钱币质量的中位数为21.7g;
故答案为:45.74,2.3,21.7;
【分析】(1)首先求出5枚古钱币的直径之和,然后除以5可得平均数,找出这5枚古钱币的厚度出现次数最多的数据可得众数,将这5枚古钱币的重量按从小到大的顺序排列,找出最中间的数据可得中位数;
(2)利用表格的形式表示出总质量、盒标质量、盒子质量,发现“鹿鹤同春”密封盒的质量异常,求出其余四个盒子质量的平均数,利用鹿鹤同春的总质量减去平均数可得实际质量.
23.【答案】(1)13
(2)解:画树状图如下:
∵有9种结果,其中2次都摸到红球的结果有1种,
∴2次都摸到红球的概率 =19 .
【解析】【解答】解:(1)共有3个球,其中红球1个,
∴摸到红球的概率等于 13 ;
故答案为:13 ;
【分析】(1)利用红球的个数除以球的总数即可;
(2)此题是抽取放回类型,画出树状图,找出总情况数以及2次都摸到红球的情况数,然后根据概率公式进行计算.
24.【答案】(1)解:方法一:由题意得 612%=50 ,
a=50×32%=16 ;
方法二:由题意得 612%=a32% ,
解得: a=16 ;
(2)解:由题意知,安全行驶速度小于等于 40×(1+10%)=44km/h .
因为该时段监测车辆样本中安全行驶的车辆占总监测车辆的占比为 50-250=4850 ,
所以估计其中安全行驶的车辆数约为: 20000×4850=19200 (辆)
【解析】【分析】(1)根据频数除以所占的比例可得总数,然后根据总数×车速为43的车辆数所占的比例可得a的值;或者根据车速为40的车辆数除以所占的比例=车速为43的车辆数除以所占的比例可得关于a的方程,求解即可;
(2)由题意知安全行驶速度小于等于40×(1+10%)=44km/h,然后求出安全行驶的车辆占总监测车辆的比例,再乘以20000即可.
25.【答案】(1)13
(2)解: 列树状图如下
一共有9种结果, 两次摸到的球的颜色为“一红一黄” 的有2种情况,
∴P(两次摸到的球的颜色为“一红一黄”)=29.
答: 两次摸到的球的颜色为“一红一黄”的概率为29.
【解析】【解答】解:∵不透明的袋子中装有红球、黄球、蓝球各一个,
∴P(摸到蓝球)=13.
故答案为:13.
【分析】(1)根据题意可知一共有3种结果数,摸到蓝球的只有1种情况,然后利用概率公式可求出摸到篮球的概率.
(2)由题意可知此事件是抽取放回,列出树状图,利用树状图可得到所有等可能的结果数及两次摸到的球的颜色为“一红一黄”的情况数,然后利用概率公式进行计算.
26.【答案】(1)3750
(2)解:从平均数看A县区和B县区的平均数一样;
从众数看,B县区不A县区好;
从中位数看A县区比B县区好.
【解析】【解答】解:(1)由题意得:5000×(30%+25%+15%+5%)=3750名.
故答案为:3750.
【分析】(1)利用A县区八年级学生的总人数×该县区八年级学生参加社会实践活动不少于3天的学生人数所占的百分之之和,列式计算可求出结果.
(2)利用表中数据从平均数,中位数,众数三个方面进行分析即可.
27.【答案】(1)抽样调查
(2)解:样本中所有学生的脂肪平均供能比为35×36.6%+25×40.4%+40×39.2%35+25+40×100%=38.59%,
样本中所有学生的碳水化合物平均供能比为35×48.0%+25×44.1%+40×47.5%35+25+40×100%=46.825%.
答:样本中的脂肪平均供能比为38.59%,碳水化合物平均供能比为46.825%.
(3)解:该校学生蛋白质平均供能比在合理的范围内,脂肪平均供能比高于参考值,碳水化合物供能比低于参考值,膳食不合理,营养搭配不均衡,建议增加碳水化合物的摄入量,减少脂肪的摄人量.(答案不唯一,建议合理即可)
【解析】【解答】解:(1)由该校1380名学生中调查了100名学生的膳食情况,
可得:本次调查采用抽样的调查方法;
故答案为:抽样;
【分析】(1)由题意可得:由该校1380名学生中调查了100名学生的膳食情况,据此可得调查方式;
(2)利用七年级的人数×B所占的比例+八年级的人数×B所占的比例+九年级的人数×B所占的比例,然后除以总人数可得样本中所有学生的脂肪平均供能比,同理可求出样本中所有学生的碳水化合物平均供能比;
(3)根据蛋白质、脂肪、碳水化合物平均供能比与参考值的关系进行分析解答.
28.【答案】(1)100;补全条形统计图如下:
(2)解:合理,理由如下:
利用样本估计总体:D占的比例为:15100=15%,
∴1500×15%=225(户),
∴ 调查小组的估计是合理的.
【解析】【解答】解:(1)本次调查的样本容量为:200.2=100(户),
∴C使用情况的户数为:100×25%=25,
D占的比例为:15100=15%,
∴B的比例为:1-25%-20%-15%=40%,
∴B使用情况的户数为:100×40%=40,
补全条形统计图如下:
故答案为:100;
【分析】(1)利用A的户数除以所占的比例可得总户数,根据C所占的比例乘以总人数可得C的户数,利用D的户数除以总户数可得所占的比例,然后根据百分比之和为1求出B所占的比例,乘以总户户数可得B的户数,据此可补全条形统计图;
(2)利用样本中D的户数除以总户数,然后乘以1500即可.
29.【答案】(1)12
(2)解:画出树状图:
共有6种结果,抽到的2张小纸条上的语句对函数的描述相符合的有①、③和①、⑤和②、④共3种,
∴抽到的2张小纸条上的语句对函数的描述相符合的概率为36=12.
【解析】【解答】解:(1)从盒子A中任意抽出1支签,抽到①的概率是12;
故答案为:12;
【分析】(1)直接根据概率公式进行计算即可;
(2)画出树状图,找出总情况数以及抽到的2张小纸条上的语句对函数的描述相符合的情况数,然后根据概率公式进行计算.
30.【答案】(1)2.8;96
(2)解:不同意,理由是:从折线统计图看,每年服务业产值的增长率都比工业产值的增长率高,因为不知道每年的具体数量和占当年的百分比,所以这五年中,每年服务业产值都比工业产值高是错误的,例如:从扇形统计图看,2019年服务业产值占“三产”的比重为45%,工业产值占“三产”的比重为49%,服务业产值低于工业产值,
∴每年服务业产值都比工业产值高是错误的.
【解析】【解答】解:(1)∵2017—2021年农业产值增长率按照从小到大排列为:
2.3%,2.7%,2.8%,2.8%,3.0%,
∴中位数为2.8%,
2019年服务业产值为:5200×45%=2340(亿元),
2020年服务业产值比2019年约增加:2340×4.1%=95.94≈96(亿元);
故答案为:2.8,96;
【分析】(1)将2017—2021年农业产值增长率按照从小到大的顺序进行排列,找出最中间的数据即为中位数;利用2019年“三产”总值乘以服务业所占的比例可得2019年服务业产值,利用2019年服务业产值乘以4.1%可得2020年服务业产值比2019年增加的钱数;
(2)由于不知道每年的具体数量和占当年的百分比,故无法计算出每年的服务业产值,据此判断
第21讲 统计与概率 2023年中考数学一轮复习专题训练(浙江专用): 这是一份第21讲 统计与概率 2023年中考数学一轮复习专题训练(浙江专用),共22页。试卷主要包含了单选题,填空题,综合题等内容,欢迎下载使用。
第16讲 对称、平移、旋转 2023年中考数学一轮复习专题训练(江苏专用): 这是一份第16讲 对称、平移、旋转 2023年中考数学一轮复习专题训练(江苏专用),共36页。试卷主要包含了单选题,填空题,作图题,综合题等内容,欢迎下载使用。
第17讲 图形的相似 2023年中考数学一轮复习专题训练(江苏专用): 这是一份第17讲 图形的相似 2023年中考数学一轮复习专题训练(江苏专用),共37页。试卷主要包含了单选题,填空题,综合题等内容,欢迎下载使用。












