安徽省安庆市怀宁县2022-2023学年九年级上学期阶段自主检测数学试卷（含答案）

这是一份安徽省安庆市怀宁县2022-2023学年九年级上学期阶段自主检测数学试卷（含答案），共8页。试卷主要包含了二次函数的图象的顶点坐标是，设A，已知二次函数y=x2-2x-2等内容，欢迎下载使用。

一．选择题(本题共10小题，每小题4分，满分 40 分)
1.下列四个函数中，一定是二次函数的是（ ）
A． B．y=ax2+bx+cC．y=x2﹣（x+7）2D．y=（x+1）（2x﹣1）
2.二次函数的图象的顶点坐标是
A．B．C．D．
3、将抛物线向右平移一个单位长度，再向上平移3个单位长度后，所得抛物线的解析式为（ ）
A、 B、 C、 D、
4.设A（-1，）、B（1，）、C（3，）是抛物线上的三个点，则、、的大小关系是（ ）
A、<< B、<< C、<< D、<<
5.若二次函数．当≤l时，随的增大而减小，则的取值范围是（ ）
A．=l B．>l C．≥l D．≤l
6.二次函数的图象如图所示，则一次函数的图象经过（ ）
A、第一、二、三象限 B、第一、二、四象限
C、第二、三、四象限 D、第一、三、四象限
7已知二次函数的与的部分对应值如下表：
则下列判断中正确的是（ ）
A．抛物线开口向上 B．抛物线与轴交于负半轴
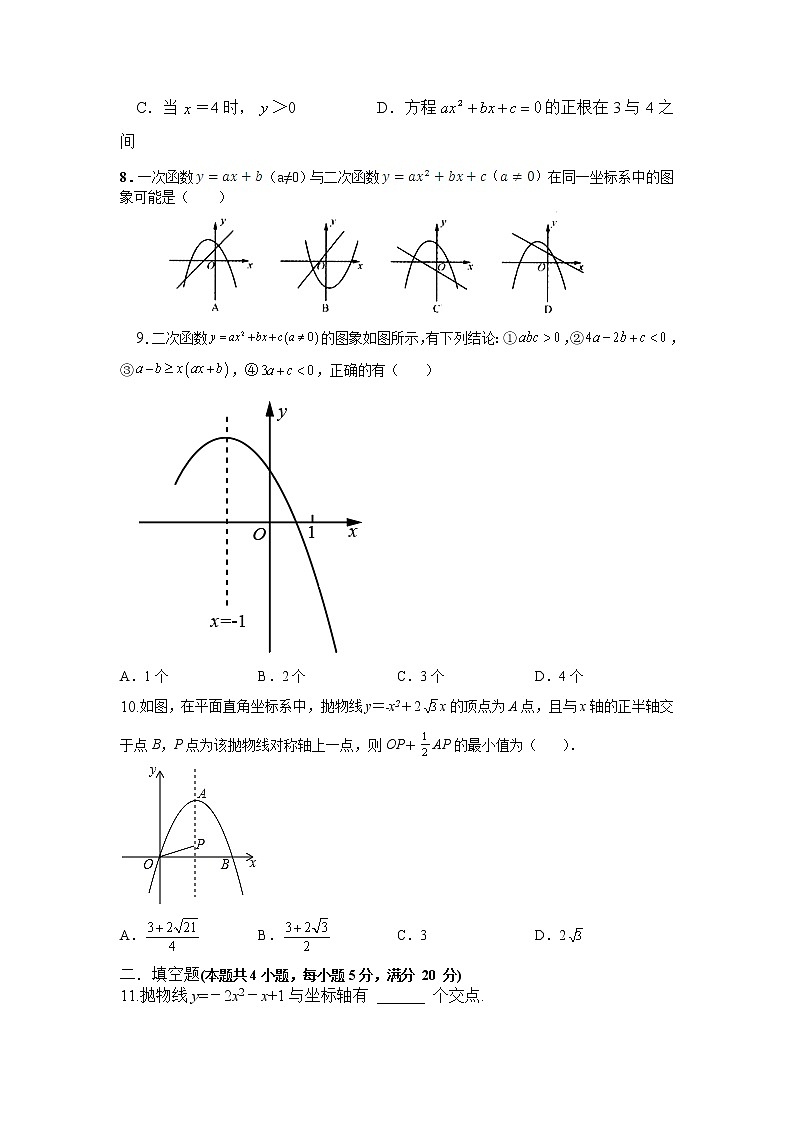
C．当＝4时，＞0 D．方程的正根在3与4之间
8．一次函数 QUOTE （a≠0）与二次函数 QUOTE 在同一坐标系中的图象可能是（ ）

9．二次函数的图象如图所示，有下列结论：①，②，③，④，正确的有（ ）
A．1个B．2个C．3个D．4个
10.如图，在平面直角坐标系中，抛物线y＝﹣x2＋2x的顶点为A点，且与x轴的正半轴交于点B，P点为该抛物线对称轴上一点，则OP＋AP的最小值为（ ）．
A．B．C．3D．2
二．填空题(本题共4小题，每小题5分，满分 20 分)
11.抛物线y=－2x2－x+1与坐标轴有 ______ 个交点.
12.二次函数y=mx2+2x+m－4m2的图象过原点，则此抛物线的顶点坐标是______.
13.已知a+b=6,ab-c2 =9.则a+b+c=______
14.二次函数y=-mx2+x+m（m为常数且m＜0）的图象经过点A（-1，n）．
（1）n=______；
（2）己知平面内有两点P（-3，1），Q（0，1），若该函数图象与线段PQ有交点，则m的取值范围是______．
三.解答题(本题共9小题，满分 90分)
（8分）已知二次函数的顶点坐标为(1，4)，且其图象经过点(－2，－5)，求此二次函数的解析式。

16.（8分）已知，二次函数y＝x2与一次函数y＝-x+2的图象交于A、B两点.
（1）请根据上述要求在下面的平面直角坐标系中画出图象；
（2）求△AOB的面积.
17.（8分）拱桥的形状是抛物线，其函数关系式为，当水面离桥顶的高度为m时，水面的宽度为多少米？

18.(8分)已知二次函数y=x2-2x-2。
（1） 求此二次函数的图象与x轴的交点坐标．
将y=x2的图象经过怎样的平移，就可以得到二次函数y=x2-2x-2的图象
19.（10分）将二次函数的图象先向右平移a个单位再向下平移2a个单位．
（1）若平移后的二次函数图象经过点，求a的值．
（2）求平移后的二次函数图象与y轴交点的纵坐标最大值
20.（10分）如图所示，抛物线与x轴交于A，B两点，与y轴交于C点，点A的坐标为（2，0），点C的坐标为（0，3），抛物线的对称轴是直线x＝－.
（1）求抛物线的解析式；
（2）M是线段AB上的任意一点，当△MBC为等腰三角形时，求点M的坐标.
21.(10分） 已知抛物线与轴的两个交点为，，与轴的交点为．
(1)直接写出不等式的解集；
(2)若点的纵坐标为．
①求a，b，c的值；
②若，求函数的最大值和最小值．
22.（12分）安庆市某公司购进某种水果的成本为20元/kg，经过市场调研发现，这种水果在未来24天的销售单价p（元/kg）与时间t（天）之间的函数关系式p=t+30（t为整数），且其日销售量y（kg）与时间t（天）的函数关系如下表．
(1)已知y与t之间的变化规律符合一次函数关系，试求此一次函数的解析式；
(2)问哪一天的销售利润最大？最大日销售利润为多少？
(3)在实际销售中，公司决定每销售1kg水果就捐赠n（n＜9）元给“精准扶贫”对象．现发现：每天扣除捐赠后的日利润随时间t的增大而增大，求n的取值范围．
22.
23 . （14分） 2022年北京冬奥会顺利召开，激起了人们对冰雪运动的极大热情，如图是某跳台滑雪训练场的横截面示意图，取某一位置的水平线为轴，过跳台A作水平线的垂线为轴，建立平面直角坐标系，图中抛物线：近似表示滑雪场地上的一座小山坡，某运动员从点正上方5米处的A点滑出，滑出后沿一段抛物线：运动．
(1)当运动员运动到离A处的水平距离为米时，离水平线的高度为5米，求抛物线的函数解析式（不要求写自变量取值范围）：
(2)在（1）的条件下，当运动员运动的水平距离为多少米时，运动员与小山坡的竖直距离为米？
(3)当运动员运动到坡顶正上方，且与坡顶距离超过米时，求的取值范围．
怀宁县2022-2023学年度第一学期阶段自主检测九年级数学试卷
参考答案
1.D 2.A 3.B 4.C 5.C 6.C 7.D 8.C 9.C 10.C
11.3 12.(-4,-4) 13.6 14. -1
15.y=-（x﹣1）2 ＋4或y=﹣x2＋2x+3
16.(1)略 （2）3
17.10米
18.（1） （1+，0）和（1-，0）
（2）向右平移1个单位，向下平移3个单位
19.．解：（1）∵二次函数的图象先向右平移a个单位再向下平移2a个单位，
∴，
∵平移后的二次函数图象经过点，
∴，
解得，
（2）∵平移后的二次函数图象与y轴交点，
∴，
∴与y轴交点的纵坐标最大值为2．
20.解答：（1）设抛物线的解析式为y＝a(x+)2+k，
把（2，0），（0，3）代入上式得：，
解得：a＝－，k＝，
∴y＝－(x+)2+，即y＝－x2－x+3，
（2）令y＝0，则－x2－x+3＝0，
解得：x1＝2，x2＝－3，∴B（－3，0），
①当CM＝BM时，∵BO＝CO＝3，
即△BOC是等腰直角三角形，
∴当M点在坐标原点O处时，△MBC是等腰三角形，∴M（0，0）；
②当BC＝BM时，在Rt△BOC中, BO＝CO＝3，
由勾股定理得：BC＝＝3，
∴BM＝3，∴M（3－3，0），
综合上述，点M的坐标为（0，0）或（3－3，0）.
21.(1)解：将不等式化为
即
该不等式的解集为当函数的值大于0时，自变量的取值范围
抛物线与轴的两个交点为，
或
(2)①点的纵坐标为，即
∵，，
∴可设，
代入得，，
∴，
∴，，．
②∵，
∴顶点坐标是，
∵，
∴，
∵，
∴当时，随增大而减小，；当时，随增大而增大，．
∴，．
22. (1)解：依题意，设y=kt+b，将(10，100)、(20，80)代入y=kt+b，
解得
∴日销售量y(kg)与时间t(天)的关系y=−2t+120(1≤t≤24)．
(2)解：设第t天的销售利润为W元，则W =（p−20）y，
当1≤t≤24时，W = ==
∴.当t=10时，W取最大值为1250
即第10天销售利润最大，最大日销售利润为1250元．
(3)解：设在前24天中每天扣除捐赠后的日销售利润为m元
由题意得
m=
=，
∴其对称轴t==，
∵在前24天中，每天扣除捐赠后的日销售利润随时间t的增大而增大
∴≥24∴n≥7
又∵n<9∴7≤n<9
23.(1) (2)4米 (3)
…
0
1
3
…
…
1
3
1
…
时间t（天）
1
3
6
10
20
…
日销售量y（kg）
118
114
108
100
80
…