数学青岛六（下）课件 本册综合 数与代数 第5课时 解决实际问题

这是一份数学青岛六（下）课件 本册综合 数与代数 第5课时 解决实际问题，共45页。

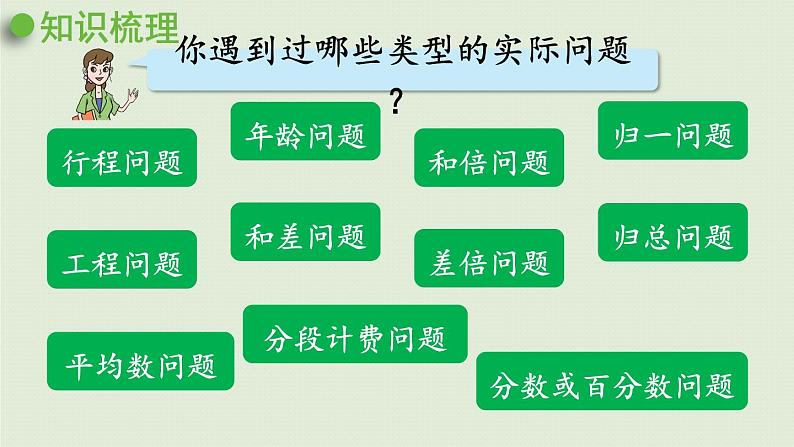
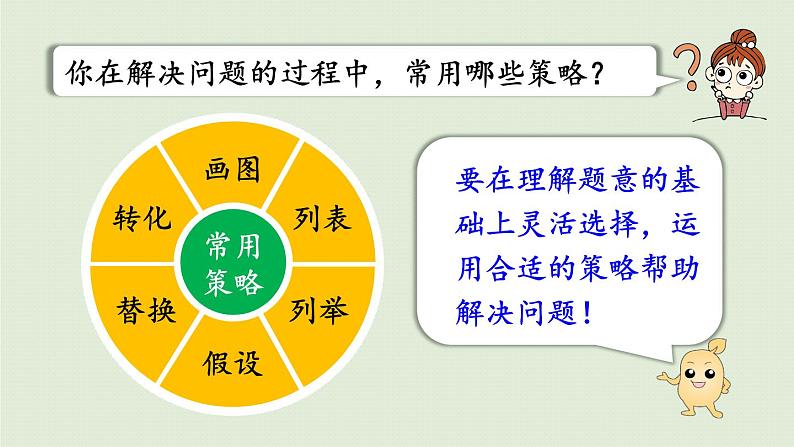
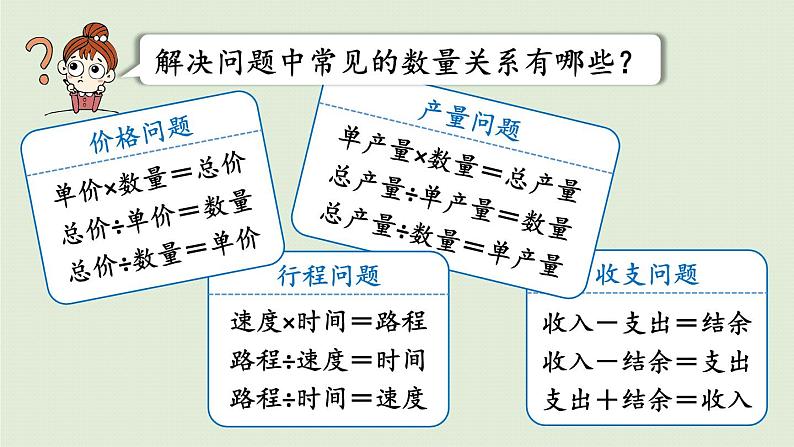
第3课时 解决实际问题 青岛版数学六年级（下）平均数问题归一问题归总问题行程问题和倍问题差倍问题和差问题年龄问题分段计费问题分数或百分数问题工程问题知识梳理你遇到过哪些类型的实际问题？ 阅读与理解：读题，理解题意，明确已知条件和所求问题。分析与解答：先分析数量关系，确定怎样算，再列式计算。回顾与反思：反思解题过程，验证答案是否正确，并写出答语。又叫顺推法，从已知信息入手“由因导果”，推想到问题。又叫逆推法，从问题着手“执因索果”，推想到已知信息。将综合法与分析法结合起来交替使用的方法。你在解决问题的过程中，常用哪些策略？常用策略解决问题中常见的数量关系有哪些？分数或百分数问题（1）求甲数是乙数的几（百）分之几。甲数÷乙数＝甲数是乙数的几（百）分之几（2）已知甲数是乙数的几（百）分之几，求甲数。乙数×几（百）分之几＝甲数（3）已知甲数是乙数的几（百）分之几，求乙数。甲数÷几（百）分之几＝乙数分数或百分数问题（4）求甲数比乙数多(少)几(百)分之几。两个数的差÷乙数＝甲数比乙数多(少)的几(百)分之几（5）已知甲数比乙数多(少)几(百)分之几，求甲数。乙数×[1±几（百）分之几]＝甲数（6）已知甲数比乙数多(少)几(百)分之几，求乙数。甲数÷[1±几（百）分之几]＝乙数折扣问题、成数问题、纳税问题、储蓄问题都可以转化为一般的百分数问题来分析解答。折扣问题成数问题储蓄问题纳税问题现价÷折扣＝原价现价÷原价＝折扣几成就是十分之几，也就是百分之几十。应纳税所得额×税率＝应纳税额利息＝本金×利率×存期原价×折扣＝现价行程问题两个物体从两地出发，相向而行，经过一段时间后相遇。两个物体同时不同地（或同地不同时或不同地不同时）出发，同向而行，后面的物体的速度快，在一定时间内能追上前面物体。相遇问题追及问题题中每份的量保持不变，解题时先求出不变的单一量，再求出未知量。主要是研究工作总量、工作时间和工作效率三者之间关系问题。工作总量=工作效率×工作时间 解题时，通常把工作总量看成单位“1”。归一问题工程问题此类题蕴含着“总量”不变，解题时，先求出总量，再求出未知量。归总问题已知大、小两个数的和与差，求这两个数分别是多少。已知两个数的差及这两个数的倍数关系，求这两个数分别是多少。和差问题差倍问题已知两个数的和及这两个数的倍数关系，求这两个数分别是多少。和倍问题 王老师要买190本《数学小词典》，单价是3.80元/本。她带了800元钱，够吗？应找回（或再付）多少元？根据解决问题的需要，怎样选择合理的计算方法？从题中，你知道了哪些数学信息？1.怎样选择合理的计算方法？ 2.怎样解决“带了800元钱，够吗？”这个问题。一想想3.80 ×190=722 (元)722 ＜800答：带800元钱够了。笔算可以解决这个问题。用简便方法口算解决这个问题。3.80 ×190= 722 (元)722 ＜800答：带800元钱够了。 3.80 × 190＝ 3.80 × 200 - 3.80 × 10＝ 760 － 38＝ 722（元）用计算器计算也可以解决这个问题。 722 ＜ 800答：带800元钱够了。3.80 ×190722 (元)= 要解决的问题是“带了800元钱够吗？”，不需要求出精确的结果，求近似值即可，所以用估算就可以解决。用估算可以解决这个问题。3.80 ×190答：带800元钱够了。3.80 ≈ 44×200 ＝ 800（元）190 ≈ 200 ≈800(元)想一想，在选择计算方法解决问题的过程中，我们经历了怎样一个过程？问题情境王老师买词典需要计算带了800元钱，够吗？应找回（或再付）多少元？只需要近似值需要精确值估算3.80≈4190≈2004×200=800口算3.80×200-3.80×10笔算3. 8 0× 1 9 0用计算器算3.80×190计算比较简单，能够快速解决问题计算结果精确，但过程相对较为复杂。计算过程简便、快捷，结果精确，但计算器携带不便。如图，要为这样一个饮料罐的外壁制作标签纸，至少需要多少纸？5×3.14×14= 219.8(平方厘米)这里用到了小数乘法计算。“图形与几何”“统计与可能性”等知识的学习是不是也要用到计算？谈谈你的看法。再如：六年级一周30节课，各学科课时占总课时的百分比如下图。一周有多少节语文课？30×23.3%≈7（节）计算在数学学习中非常重要，大部分的知识要用到计算。这里用到了分数乘法计算。课堂练习1.小刚和小明分别从书店和学校同时出发去体育馆。小刚平均每分钟走60米。如果两人要同时到达，小明平均每分钟要走多少米?360÷60=6(分)240÷6=40(米)答：小明平均每分钟走40米。360米240米教材第91页“应用与反思”第7题“两人同时到达体育馆”表示两人走的时间是一样的，先根据“时间＝路程（360）÷速度（60）”求出所需时间，再根据“速度＝路程（240）÷时间”求出小明的速度。2.一列火车从A城开往B城。如果速度是120千米/时，则4小时可以到达;如果速度是160千米/时，几小时可以到达?120×4÷160=3(时)答：3小时可以到达。教材第91页“应用与反思”第8题先求出路程，路程是不变量，再根据“时间＝路程÷速度”求出提速后所需的时间。教材第91页“应用与反思”第9题3.学校食堂计划购买1500千克大米。(1)如果平均每天吃95千克，这些大米够吃半个月吗? (一个月按30天计算)(2)如果够了，还剩下多少千克?如果不够，还需要购进多少千克?要解答“这些大米够不够吃半个月”的问题，需要估算还是精确计算?要解答“剩下多少千克”或“需要购进多少千克”的问题呢?3.学校食堂计划购买1500千克大米。(1)如果平均每天吃95千克，这些大米够吃半个月吗? (一个月按30天计算)这些大米够吃半个月吗？只需要近似值估算：95≈100 100×15=1500（千克）答：够了。教材第91页“应用与反思”第9题因为把95估成100时，数变大了，所以估算的积大于实际的积,也就是说实际半个月吃不了1500千克大米。因此，这些大米够吃半个月。3.学校食堂计划购买1500千克大米。(2)如果够了，还剩下多少千克?如果不够，还需要购进多少千克?教材第91页“应用与反思”第9题还剩下（还需要购进）多少千克？需要精确计算先求半个月需要多少千克大米：95×（30÷2）=1425（千克）再求还剩下多少千克：1500-1425=75(千克)答：还剩下75千克。教材第91页“应用与反思”第10题4.下面是王阿姨某天卖出报刊情况记录表。(1)《都市晚报》和《京华晨报》一共卖了多少元?总价=单价×数量(1)0.50×90+0.30×85=70.50(元)答：一共卖了70.5元。4.下面是王阿姨某天卖出报刊情况记录表。(2) 《电脑世界》和《城市生活》哪种卖的钱多?多多少元?教材第91页“应用与反思”第10题总价=单价×数量(2)《电脑世界》：1.85×25=46.25(元)《城市生活》：5.70×9=51.30(元) 46.25<51.3051.30-46.25=5.05(元)答：《城市生活》卖的钱多，比《电脑世界》多5.05元。教材第92页“应用与反思”第11题 答：参加越野比赛的男生有70人。  教材第92页“应用与反思”第12题 请根据上面的信息填表。303628426  教材第92页“应用与反思”第13题7. (1)质监局对全市儿童服装产品进行质量抽检。在抽检的产品中有48个品牌产品合格,有2个品牌产品不合格。本次抽检的合格率是多少?48÷(48+2)×100%=96%答：本次抽检的合格率是96%。合格率＝合格数÷总数教材第92页“应用与反思”第13题8. (2)大豆的出油率是18%。现有250千克大豆，能榨出50千克豆油吗?250×18%=45(千克)45＜50答：250千克大豆不能榨出50千克豆油。榨出的油的质量＝大豆的质量×出油率教材第92页“应用与反思”第14题9.一种“感冒通”片的两种主要药物成分是人工牛黄( 12%)和马来酸氯苯那敏( 2%)。制药厂要配制5000克这样的“感冒通”片，这两种药物分别需要多少克?解决上面的问题需要精确计算吗?需要人工牛黄：5000×12%=600(克)马来酸氯苯那敏：5000×2%=100(克)教材第93页“应用与反思”第16题10. 大连、烟台两个港口相距87海里。 甲、乙两船分别从两个港口同时出发，相向而行，3小时后相遇。乙船每小时行15海里，甲船每小时行多少海里?87÷3-15=14(海里)答：甲船每小时行驶14海里。所求问题是“甲船每小时行多少海里？”，需要求出确切的速度，所以要精确计算。速度和=路程÷相遇时间教材第93页“应用与反思”第17题11. (1) 2017年1月9日，王平的爸爸在银行存了20000元钱，定期一年，年利率是1.75%。 到期后应得利息多少元?20000×1.75%×1=350(元)答：到期后应得利息350元。利息＝本金×利率×存期教材第93页“应用与反思”第17题(2)一种上衣原价为120元，现按七折销售，便宜了多少元?120-120×70%=36(元)答：便宜了36元。几折就是十分之几，也就是百分之几十。原价×折扣＝现价教材第93页“应用与反思”第17题(3)商场12月份销售的女装数量比男装多25%，男装销售了1280件，女装销售了多少件?1280×(1+25%)=1600(件)答：女装销售了1600件。男装销售件数×25%＝女装比男装多销售的件数女装销售件数=男装销售件数+女装比男装多销售的件数教材第93页“应用与反思”第18题12. 李大爷家养的鸡、鸭、鹅共3000只。3000×30%-3000×18%=360(只)答：鸭比鹅多360只。鸭比鹅多多少只?教材第93页“应用与反思”第19题  答：还剩下352米没有修。教材第93页“应用与反思”第20题14.下表是A、B、C三个城市绿化面积的有关信息。哪个城市的绿化情况好一些？直接比较绿化面积能反映三个城市的绿化情况吗?应该比较它们的绿化率.....教材第93页“应用与反思”第20题 因为A、B、C三个城市的总面积不同,所以直接比较绿化面积不能反映三个城市的绿化情况,应该比较它们的绿化率。答：A城市的绿化情况好一些。32.9%＞22.7%＞18%A城市:0.23÷0.7×100%≈32.9%B城市:0.25÷1.1×100%≈22.7%C城市:0.27÷1.5×100%≈18%教材第93页“应用与反思”第21题15.超市有鸡蛋40箱、鸭蛋30箱，共重275千克。已知1箱鸡蛋的质量和2箱鸭蛋的质量相等，1箱鸡蛋的质量是多少千克?1箱鸭蛋的质量：275÷(40×2+30)=2.5(千克)1箱鸡蛋的质量：2.5×2=5(千克)答：一箱鸡蛋的质量是5千克。假设全部是鸭蛋，则鸭蛋共有（ 40×2+30 ）箱，根据 “总质量÷箱数=1箱的质量”先求出1箱鸭蛋的质量。思路一教材第93页“应用与反思”第21题15.超市有鸡蛋40箱、鸭蛋30箱，共重275千克。已知1箱鸡蛋的质量和2箱鸭蛋的质量相等，1箱鸡蛋的质量是多少千克?1箱鸡蛋的质量：275÷(40+30÷2)=5(千克)答：一箱鸡蛋的质量是5千克。假设全部是鸡蛋，则鸡蛋共有（ 40+30÷2 ）箱，根据 “总质量÷箱数=1箱的质量”求出1箱鸡蛋的质量。思路二课后作业