

(新高考)高考数学二轮复习讲义11《圆锥曲线的方程与性质》(解析版)
展开11 圆锥曲线的方程与性质
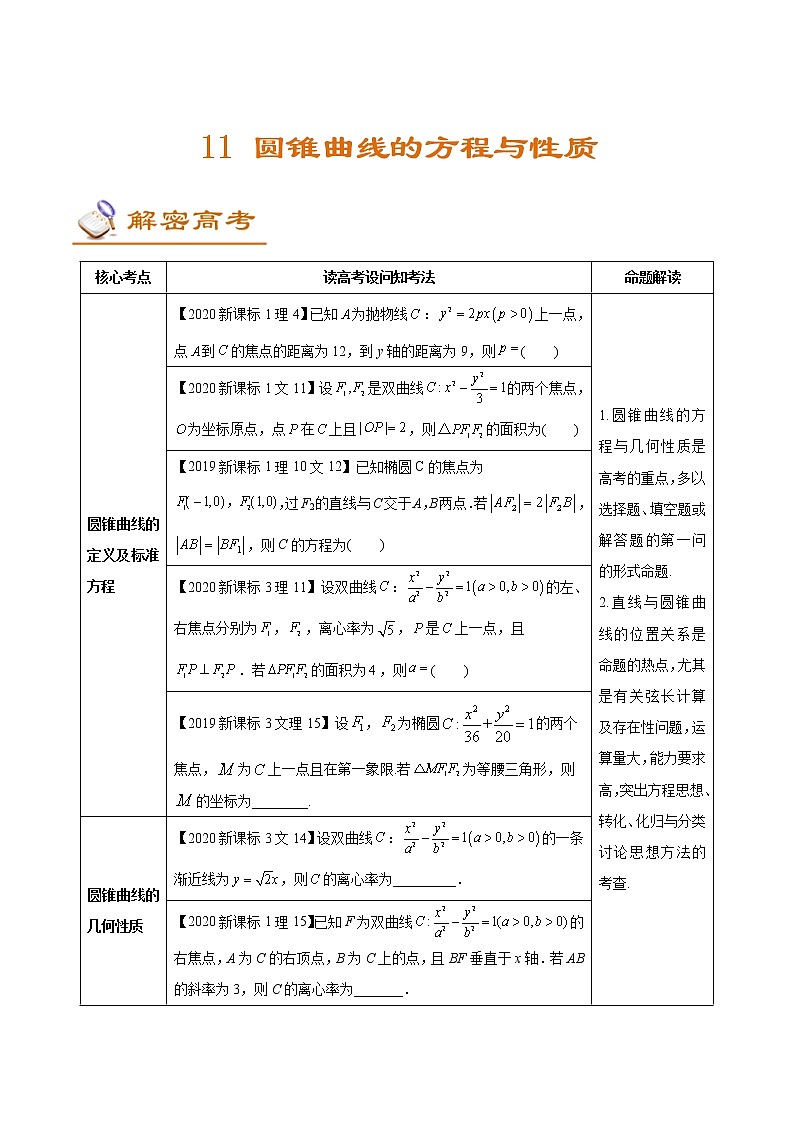
核心考点 | 读高考设问知考法 | 命题解读 |
圆锥曲线的定义及标准方程 | 【2020新课标1理4】已知为抛物线:上一点,点到的焦点的距离为12,到y轴的距离为9,则( ) | 1.圆锥曲线的方程与几何性质是高考的重点,多以选择题、填空题或解答题的第一问的形式命题. 2.直线与圆锥曲线的位置关系是命题的热点,尤其是有关弦长计算及存在性问题,运算量大,能力要求高,突出方程思想、转化、化归与分类讨论思想方法的考查. |
【2020新课标1文11】设是双曲线的两个焦点,为坐标原点,点在上且,则的面积为( ) | ||
【2019新课标1理10文12】已知椭圆C的焦点为,过F2的直线与C交于A,B两点.若,,则C的方程为( ) | ||
【2020新课标3理11】设双曲线:的左、右焦点分别为,,离心率为,是上一点,且.若的面积为,则( ) | ||
【2019新课标3文理15】设,为椭圆的两个焦点,为上一点且在第一象限.若为等腰三角形,则的坐标为________. | ||
圆锥曲线的几何性质 | 【2020新课标3文14】设双曲线:的一条渐近线为,则的离心率为_________. | |
【2020新课标1理15】已知F为双曲线的右焦点,A为C的右顶点,B为C上的点,且BF垂直于x轴.若AB的斜率为3,则C的离心率为_______. | ||
【2019新课标1理16】已知双曲线C:的左、右焦点分别为F1,F2,过F1的直线与C的两条渐近线分别交于A,B两点.若,,则C的离心率为________. | ||
【2016新课标3文12理11】已知为坐标原点,是椭圆:的左焦点,分别为的左右顶点,为上一点,且轴.过点的直线与线段交于点,与轴交于点,若直线经过的中点,则的离心率为( ) | ||
直线与圆锥曲线的综合问题 | 【2013新课标1理10】已知椭圆的右焦点为,过点的直线交椭圆于两点,若的中点坐标为,则椭圆的方程为( ) | |
【2020新高考全国13】斜率为的直线过抛物线:的焦点,且与交于,两点,则=_______. | ||
【2019新课标1理19】已知抛物线C:的焦点为F,斜率为的直线l与C的交点为A,B,与x轴的交点为P.(1)若,求l的方程;(2)若,求. | ||
【2020新高考全国Ⅱ卷21】已知椭圆:过点,点为其左顶点,且的斜率为 ,(1)求的方程;(2)点为椭圆上任意一点,求的面积的最大值. | ||
(2020·天津卷)已知椭圆+=1(a>b>0)的一个顶点为A(0,-3),右焦点为F,且|OA|=|OF|,其中O为原点.(1)求椭圆的方程;(2)已知点C满足3=,点B在椭圆上(B异于椭圆的顶点),直线AB与以C为圆心的圆相切于点P,且P为线段AB的中点,求直线AB的方程. |
核心考点一 圆锥曲线的定义及标准方程
1.圆锥曲线的定义
(1)椭圆:|MF1|+|MF2|=2a(2a>|F1F2|);
(2)双曲线:||MF1|-|MF2||=2a(2a<|F1F2|);
(3)抛物线:|MF|=d(d为M点到准线的距离).
温馨提醒 应用圆锥曲线定义解题时,易忽视定义中隐含条件导致错误.
2.圆锥曲线的标准方程
(1)椭圆:+=1(a>b>0)(焦点在x轴上)或+=1(a>b>0)(焦点在y轴上);
(2)双曲线:-=1(a>0,b>0)(焦点在x轴上)或-=1(a>0,b>0)(焦点在y轴上);
(3)抛物线:y2=2px,y2=-2px,x2=2py,x2=-2py(p>0).
1.【2020新课标1理4】已知为抛物线:上一点,点到的焦点的距离为12,到y轴的距离为9,则( )
A.2 B.3 C.6 D.9
【解析】设抛物线的焦点为F,由抛物线的定义知,即,解得.
故选C.
2.【2020新课标1文11】设是双曲线的两个焦点,为坐标原点,点在上且,则的面积为( )
A. B.3 C. D.2
【解析】方法1:不妨设,则,因为,所以点在以为直径的圆上,即是以P为直角顶点的直角三角形,故,
又,所以,
解得,所以,故选B.
方法2:点的轨迹方程为,联立,解得(得到点的纵坐标),所以,故选B.
方法3:由二级结论焦点三角形的面积为,故选B.
3.【2019新课标1理10文12】已知椭圆C的焦点为,过F2的直线与C交于A,B两点.若,,则C的方程为( )
A. B. C. D.
【解法1】可以运用下面方法求解:如图,由已知可设,则,由椭圆的定义有.在和中,由余弦定理得,又互补,,两式消去,得,解得.
所求椭圆方程为,故选B.
【解法2】如图,由已知可设,则,由椭圆的定义有
.在中,由余弦定理推论得
.在中,由余弦定理得,解得.所求椭圆方程为,故选B.
【解法3】由利用向量或相似三角形的性质得点,代入椭圆方程得,所以,,故选B.
【解法4】由椭圆的极坐标方程得得,再利用余弦定理得出关于的方程.
4.【2020新课标2理19】已知椭圆:的右焦点与抛物线的焦点重合,的中心与的顶点重合.过且与轴垂直的直线交于两点,交于两点,且.
(1)求的离心率;
(2)设是与的公共点,若,求与的标准方程.
【解析】(1),轴且与椭圆相交于、两点,则直线的方程为,
联立,解得,则,
抛物线的方程为,联立,解得,,
,即,,即,即,
,解得,因此椭圆的离心率为;
(2)由(1)知,,椭圆的方程为,
联立,消去并整理得,解得或(舍去),
由抛物线的定义可得,解得.
因此,曲线的标准方程为,曲线的标准方程为.
1.【2020新课标3文7理5】设为坐标原点,直线与抛物线C:交于,两点,若,则的焦点坐标为( )
A. B. C. D.
【解析】因为与抛物线交于两点,且,根据抛物线的对称性可以确定,所以,代入抛物线方程,求得,所以其焦点坐标为,故选B.
2.【2020新课标3理11】设双曲线:的左、右焦点分别为,,离心率为,是上一点,且.若的面积为,则( )
A.1 B.2 C.4 D.8
【解析】方法1:,,根据双曲线的定义可得,
,即,
,,
,即,解得,故选A.
方法2:的面积为,离心率,所以,故选A.
3.【2019新课标3文理15】设,为椭圆的两个焦点,为上一点且在第一象限.若为等腰三角形,则的坐标为___________.
【解析】由已知可得,
.∴.
设点的坐标为,则,
又,解得,
,解得(舍去),的坐标为.
核心考点二 圆锥曲线的几何性质
圆锥曲线的重要性质:
(1)椭圆、双曲线中a,b,c之间的关系
①在椭圆中:a2=b2+c2;离心率为e==.
②在双曲线中:c2=a2+b2;离心率为e==.
(2)双曲线的渐近线方程与焦点坐标
①双曲线-=1(a>0,b>0)的渐近线方程为y=±x;焦点坐标F1(-c,0),F2(c,0).
②双曲线-=1(a>0,b>0)的渐近线方程为y=±x,焦点坐标F1(0,-c),F2(0,c).
(3)抛物线的焦点坐标与准线方程
①抛物线y2=2px(p>0)的焦点F,准线方程x=-.
②抛物线x2=2py(p>0)的焦点F,准线方程y=-.
1.【2020新课标1理15】已知F为双曲线的右焦点,A为C的右顶点,B为C上的点,且BF垂直于x轴.若AB的斜率为3,则C的离心率为_______.
【解析】联立,解得,所以.依题可得,,
即,变形得,因此的离心率为.故答案为.
2.【2016新课标3文12理11】已知为坐标原点,是椭圆:的左焦点,分别为的左右顶点,为上一点,且轴.过点的直线与线段交于点,与轴交于点,若直线经过的中点,则的离心率为( )
(A) (B) (C) (D)
【解析】解法1:由题意设直线的方程为,分别令与得,,由,得,即,整理得,所以椭圆离心率为,故选A。
解法2:设,则直线的方程为,由题意可知, 和三点共线,则,化简得,则的离心率.故选A.
3.(多选题)已知椭圆Ω:+=1(a>b>0),则下列结论正确的是( )
A.若a=2b,则椭圆Ω的离心率为
B.若椭圆Ω的离心率为,则=
C.若点F1,F2分别为椭圆Ω的左、右焦点,直线l过点F1且与椭圆Ω交于A,B两点,则△ABF2的周长为4a
D.若点A1,A2分别为椭圆Ω的左、右顶点,点P为椭圆Ω上异于点A1,A2的任意一点,则直线PA1,PA2的斜率之积为-
【解析】若a=2b,则c=b,所以e=,A不正确;若e=,则a=2c,b=c,所以=,B正确;根据椭圆的定义易知C正确;设点P(x0,y0),则+=1,易知A1(-a,0),A2(a,0),所以直线PA1,PA2的斜率之积是·===-,D正确.故选BCD.
1.【2020新课标3文14】设双曲线:的一条渐近线为,则的离心率为_________.
【解析】由双曲线方程可得其焦点在轴上,因为其一条渐近线为,所以,.故答案为.
2.【2019新课标1理16】已知双曲线C:的左、右焦点分别为F1,F2,过F1的直线与C的两条渐近线分别交于A,B两点.若,,则C的离心率为____________.
【解析】如图,由得又得OA是三角形的中位线,即由,得则有,
又OA与OB都是渐近线,得又,得.又渐近线OB的斜率为,所以该双曲线的离心率为.
3.(多选题)双曲线C:-=1的右焦点为F,点P在双曲线C的一条渐近线上,O为坐标原点,则下列说法正确的是( )
A.双曲线C的离心率为
B.双曲线-=1与双曲线C的渐近线相同
C.若PO⊥PF,则△PFO的面积为
D.|PF|的最小值为2
【解析】对于A,因为a=2,b=,所以c==,所以双曲线C的离心率为,所以A正确;对于B,它们的渐近线都是直线y=±x,所以B正确;对于C,结合PO⊥PF,点P在双曲线C的一条渐近线上,不妨设点P在渐近线y=x上,则直线PF的方程为y-0=-(x-),即y=-(x-),由解得所以点P,所以△PFO的面积S=××=,所以C正确;对于D,因为点F(,0),双曲线C的一条渐近线为直线y=x,所以|PF|的最小值就是点F到渐近线的距离,为,所以D错误.故选ABC.
核心考点三 直线与圆锥曲线综合问题
1.直线与圆锥曲线相交的弦:
设而不求,利用根与系数的关系,进行整体代入.即当斜率为k,直线与圆锥曲线交于A(x1,y1),B(x2,y2)时,|AB|=|x1-x2|==.
2.过抛物线焦点的弦:
抛物线y2=2px(p>0)过焦点F的弦AB,若A(x1,y1),B(x2,y2),则x1x2=,y1y2=-p2,
弦长|AB|=x1+x2+p.
1.【2020新高考全国13】斜率为的直线过抛物线:的焦点,且与交于,两点,则=_______.
【解析】,代入抛物线方程得,
,故答案为.
2.【2019新课标1理19】已知抛物线C:的焦点为F,斜率为的直线l与C的交点为A,B,与x轴的交点为P.(1)若,求l的方程;(2)若,求.
【解析】(1)设直线方程为:,,
由抛物线焦半径公式可知:
联立,得
则
,解得
直线的方程为:,即
(2)设直线方程为:,
联立,得,则
,
,
则
3.【2020新高考全国Ⅱ卷21】已知椭圆:过点,点为其左顶点,且的斜率为 ,(1)求的方程;(2)点为椭圆上任意一点,求的面积的最大值.
【解析】(1)由题意可知直线AM的方程为:,即.
当时,解得,所以,
椭圆过点,可得,解得.
所以的方程为:.
(2)设与直线平行的直线方程为:,
如图所示,当直线与椭圆相切时,与距离比较远的直线与椭圆的切点为,此时的面积取得最大值.
联立直线方程与椭圆方程,
可得,即,
所以,即,解得,
与AM距离比较远的直线方程:,
直线AM方程为:,
点N到直线AM的距离即两平行线之间的距离,即,
由两点之间距离公式可得.
所以△AMN的面积的最大值为:.
1.【2013新课标1理10】已知椭圆的右焦点为,过点的直线交椭圆于两点,若的中点坐标为,则椭圆的方程为( )
A、 B、 C、 D、
【解析】设,则,=-2,
① ②
由①减②得:,
∴===,又==,∴=,又9==,解得=9,=18,∴椭圆方程为,故选D.
2.【2010新课标理20】设分别是椭圆的左、右焦点,过斜率为1的直线与相交于两点,且成等差数列,
(1)求的离心率; (2) 设点满足,求椭圆的方程.
【解析】(I)由椭圆定义知,又,得
的方程为,其中.
设,,则A、B两点坐标满足方程组
化简的
则
因为直线AB斜率为1,所以
得故
所以E的离心率
(II)设AB的中点为,由(I)知,.
由,得,即得,从而
故椭圆E的方程为.
3.【2020天津卷】已知椭圆+=1(a>b>0)的一个顶点为A(0,-3),右焦点为F,且|OA|=|OF|,其中O为原点.
(1)求椭圆的方程;
(2)已知点C满足3=,点B在椭圆上(B异于椭圆的顶点),直线AB与以C为圆心的圆相切于点P,且P为线段AB的中点,求直线AB的方程.
【解析】(1)由已知得b=3.记半焦距为c,
由|OF|=|OA|,得c=b=3.
由a2=b2+c2,得a2=18.
所以椭圆的方程为+=1.
(2)因为直线AB与以C为圆心的圆相切于点P,所以AB⊥CP.
依题意,直线AB和直线CP的斜率均存在,
设直线AB的方程为y=kx-3.联立
消去y,可得(2k2+1)x2-12kx=0,解得x=0或x=.
依题意,可得点B的坐标为.
因为P为线段AB的中点,点A的坐标为(0,-3),
所以点P的坐标为.
由3=,得点C的坐标为(1,0),
故直线CP的斜率kCP==.
又因为AB⊥CP,所以k·=-1,
整理得2k2-3k+1=0,解得k=或k=1.
所以,直线AB的方程为y=x-3或y=x-3.
即直线AB的方程为x-2y-6=0或x-y-3=0.
专题11 圆锥曲线的定义、方程与性质- 2022届高考数学二模试题分类汇编(新高考卷)(解析版): 这是一份专题11 圆锥曲线的定义、方程与性质- 2022届高考数学二模试题分类汇编(新高考卷)(解析版),共14页。
高中数学高考解密11 圆锥曲线的方程与性质(分层训练)-【高频考点解密】2021年新高考数学二轮复习讲义+分层训练(原卷版): 这是一份高中数学高考解密11 圆锥曲线的方程与性质(分层训练)-【高频考点解密】2021年新高考数学二轮复习讲义+分层训练(原卷版),共3页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
高中数学高考解密11 圆锥曲线的方程与性质(讲义)-【高频考点解密】2021年新高考数学二轮复习讲义+分层训练: 这是一份高中数学高考解密11 圆锥曲线的方程与性质(讲义)-【高频考点解密】2021年新高考数学二轮复习讲义+分层训练,共14页。












