
2021眉山东坡区多悦高级中学校高一上学期期中考试数学试题含答案
展开多悦高中2023届半期考试
数 学 试题
2020.11.10
本试卷分选择题和非选择题两部分。第Ⅰ卷(选择题)1至2页,第Ⅱ卷 (非选择题)3至4页,共4页,满分150分,考试时间120分钟。
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合,,则集合( )
A.0 B. C. D.
2.设全集U=R,集合,集合,则等于( )
A.{1,3,2,6} B.{(1,3),(2,6)} C.M D.{3,6}
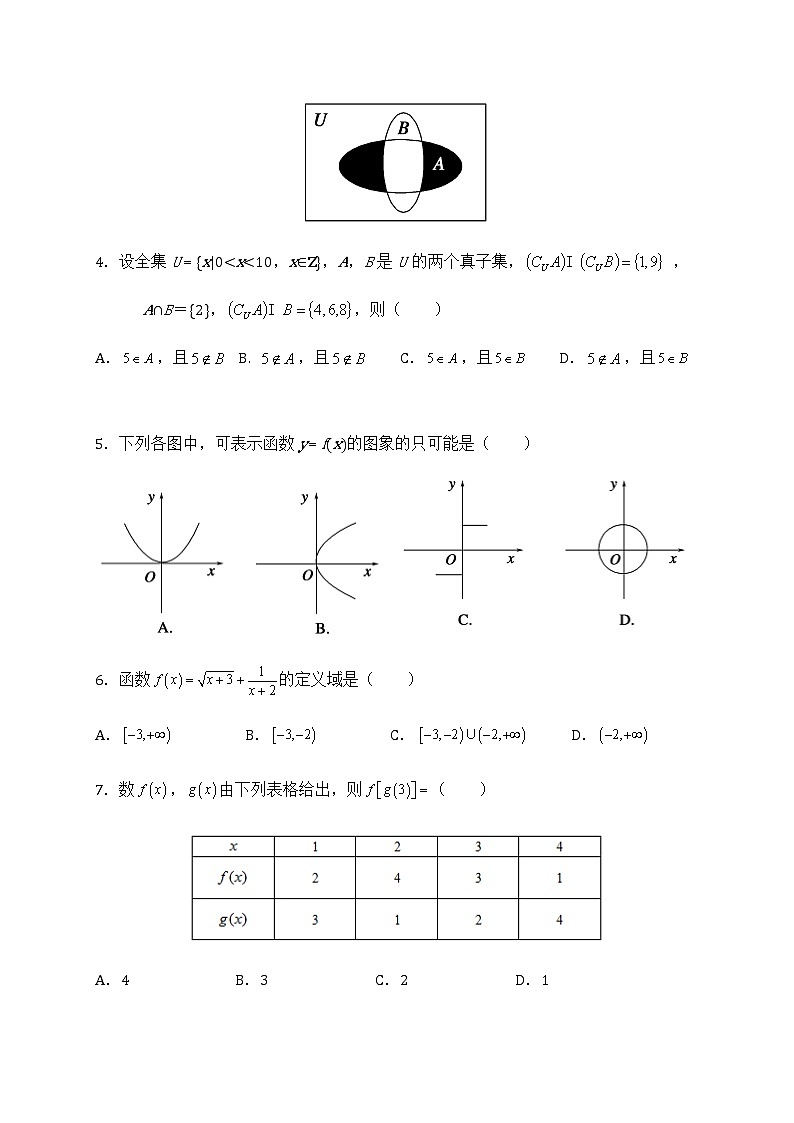
3.如图所示,阴影部分表示的集合是( )
A. B. C. D.
4.设全集U{x|0<x<10,x∈Z},A,B是U的两个真子集, ,
A∩B={2},,则( )
A.,且 B. ,且 C.,且 D.,且
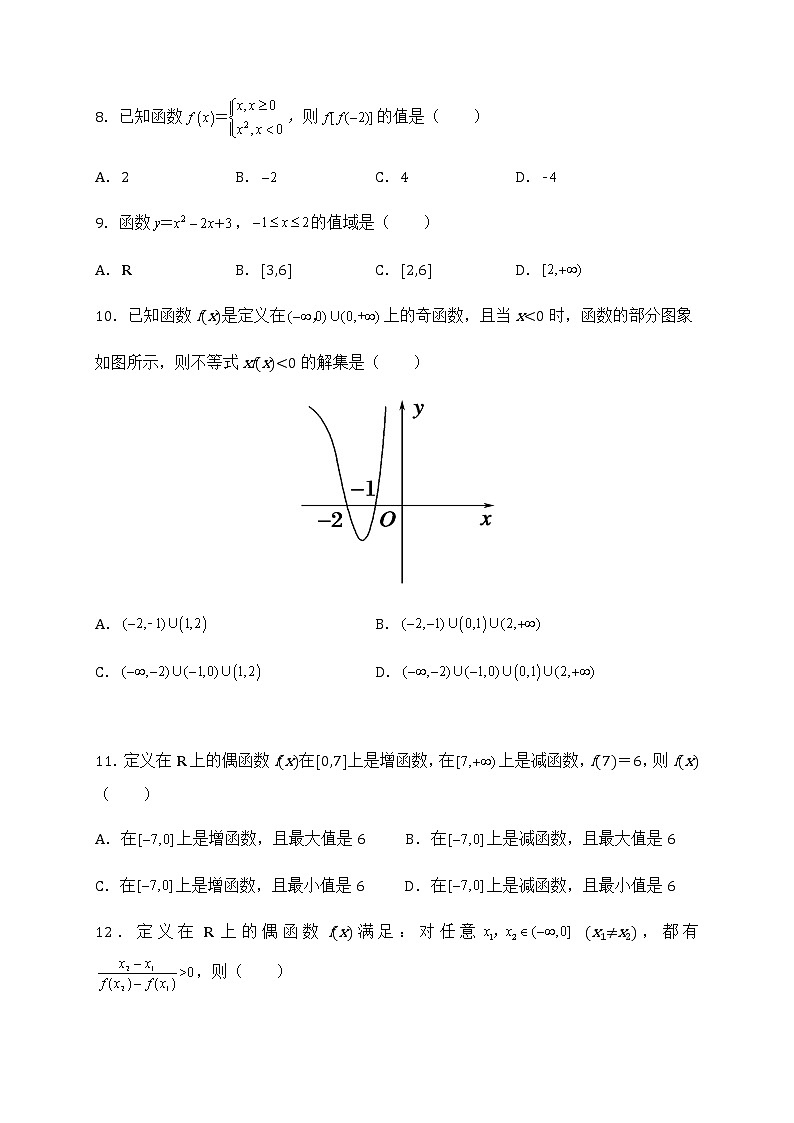
5.下列各图中,可表示函数yf(x)的图象的只可能是( )
6.函数的定义域是( )
A. B. C. D.
7.数,由下列表格给出,则( )
A.4 B.3 C.2 D.1
8.已知函数,则的值是( )
A.2 B. C.4 D.
9.函数,的值域是( )
A.R B.[3,6] C.[2,6] D.
10.已知函数f(x)是定义在上的奇函数,且当x<0时,函数的部分图象
如图所示,则不等式xf(x)<0的解集是( )
A. B.
C. D.
11.定义在R上的偶函数f(x)在[0,7]上是增函数,在上是减函数,f(7)=6,则f(x)( )
A.在上是增函数,且最大值是6 B.在上是减函数,且最大值是6
C.在上是增函数,且最小值是6 D.在上是减函数,且最小值是6
12.定义在R上的偶函数f(x)满足:对任意 (x1≠x2),都有,则( )
A.<f(4)<f(6) B.f(4)<<f(6)
C.f(6)<<f(4) D.f(6)<f(4)<
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.设P和Q是两个集合,定义集合,若P={1,2,3,4},则________.
14.函数的单调递减区间是________.
15.若函数是偶函数,则的递减区间是________.
16.设函数,则函数y=,y= 的图象交点个数是________.
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(10分)已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,;
(2)若,求a的取值范围.
18.(12分)设A={x|x22(a1)xa21=0},,x∈Z}.
若A∩B=A,求a的取值范围.
19.(12分)已知函数f(x)=2xm,其中m为常数.
(1)求证:函数f(x)在R上是减函数;
(2)当函数f(x)是奇函数时,求实数m的值.
20.(12分)已知函数f(x)是正比例函数,函数g(x)是反比例函数,且f(1)=1,g(1)=2,
(1)求函数f(x)和g(x);
(2)判断函数f(x)g(x)的奇偶性.
21.(12分)经过市场调查,超市中的某种小商品在过去的近40天的日销售量(单位:件)与价格(单位:元)为时间(单位:天)的函数,且日销售量近似满足,价格近似满足.
(1)写出该商品的日销售额(单位:元)与时间()的函数解析式并用分段函数形式表示该解析式(日销售额=销售量商品价格);
(2)求该种商品的日销售额的最大值和最小值.
22.(12分)函数f(x)=是定义在上的奇函数,且.
(1)求f(x)的解析式;
(2)证明f(x)在上为增函数;
(3)解不等式f(t1)f(t)<0.
多悦高中2023届第一期半期考试
数 学 答 案
一、选择题
1.【答案】C
【解析】因为集合,,所以,故选C.
2.【答案】C
【解析】,N=R..故选C.
3.【答案】A
【解析】因为阴影部分既在集合中又在集合A中,
所以阴影部分为,故选A.
4.【答案】A
【解析】可借助Venn图(如图2)解决,数形结合.故选A.
图2
5.【答案】A
【解析】根据函数的概念知,只有“一对一”或“多对一”对应才能构成函数关系.
故选A.
6.【答案】C
【解析】由题可得:且,故选C.
7.【答案】A
【解析】由表可知,,故选A.
8.【答案】C
【解析】∵,而,∴.
又4>0,∴.故选C.
9.【答案】C
【解析】画出函数,的图象,如图3所示,观察函数的图象可得图象上所有点的纵坐标的取值范围是[2,6],所以值域是[2,6].故选C.
10.【答案】D
【解析】xf(x)<0⇔x与f(x)异号,由函数图象及奇偶性易得结论.故选D.
11.【答案】B
【解析】∵f(x)是偶函数,∴f(x)的图象关于y轴对称.
∴f(x)在上是减函数,且最大值为6.故选B.
12.【答案】C
【解析】∵对任意(x1≠x2),都有,
∴对任意,若x1<x2,总有f(x1)<f(x2),
∴f(x)在上是增函数.∴.
又∵函数f(x)是偶函数,∴,,
∴f(6)<<f(4).故选C.
二、填空题
13.【答案】{4}
【解析】因为,所以,
故,故{4}.
14.【答案】
【解析】由,得x≥1或,
∴函数减区间为.
15.【答案】
【解析】∵f(x)是偶函数,∴.
∴.∴f(x)=x22,其递减区间为.
16.【答案】4
【解析】函数y=f(x)的图象如图5所示,
则函数y=f(x)与y=的图象的交点个数是4.
图5
三、解答题
17.【答案】(1),={x|1<x<2};(2)a<8.
【解析】(1)A∪B={x|2≤x≤8}∪{x|1<x<6}={x|1<x≤8}.
={x|x<2或x>8}.∴={x|1<x<2}.
(2)∵,∴a<8.
18.【答案】.
【解析】由,x∈Z},得.
由A∩B=A,得A⊆B.于是,A有四种可能,
即,,A={0},.
以下对A分类讨论:
(1)若,则Δ=4(a1)24a24=8a8<0,解得a<1;
(2)若,则Δ=8a8=0,解得a=1.
此时x22(a1)xa21=0可化为x2=0,
所以x=0,这与x=4是矛盾的;
(3)若A={0},则由(2)可知,a=1;
(4)若A={4,0},则,解得a=1.
综上可知,a的取值范围.
19.【答案】(1)见解析;(2)0.
【解析】(1)证明:设x1,x2是R上的任意两个实数,且x1<x2,
则f(x1)-f(x2)=(2x1m)=2(x2x1),
∵x1<x2,∴x2x1>0.∴f(x1)>f(x2)
∴函数f(x)在R上是减函数.
(2)∵函数f(x)是奇函数,
∴对任意x∈R,有f(x)=f(x).
∴2xm=(2xm).∴m=0.
20.【答案】(1)f(x)=x,g(x)=;(2)奇函数.
【解析】(1)设,g(x)=,其中k1k2≠0.
∵f(1)=1,g(1)=2,∴,.
∴k1=1,k2=2.∴f(x)=x,g(x)=.
(2)设h(x)=f(x)g(x),则,
∴函数h(x)的定义域是.
∵h(x)=x==h(x),
∴函数h(x)是奇函数,即函数f(x)g(x)是奇函数.
21.【答案】(1)由题意知
.
(2)当时,在区间上单调递减,故;当时,在区间上单调递增,在区间上单调递减,故
当时,取最小值,当时,取最大值.
22.【答案】(1)f(x)=;(2)见解析;(3).
【解析】(1)由题意得,
解得,所以f(x)=.
(2)证明:任取两数x1,x2,且1<x1<x2<1,
则.
因为1<x1<x2<1,所以x1x2<0,x1x2<1,故1x1x2>0,
所以f(x1)f(x2)<0,故f(x)在上是增函数.
(3)因为f(x)是奇函数,所以由f(t1)+f(t)<0,得f(t1)<f(t)=f(t).
由(2)知,f(x)在上是增函数,
所以1<t1<t<1,解得0<t<,
所以原不等式的解集为.
四川省眉山市东坡区多悦高级中学校2020-2021学年高一上学期期中考试数学试题 Word版含答案: 这是一份四川省眉山市东坡区多悦高级中学校2020-2021学年高一上学期期中考试数学试题 Word版含答案,共12页。试卷主要包含了选择题的作答,非选择题的作答,函数的定义域是,数,由下列表格给出,则,已知函数,则的值是,函数,的值域是,故选C等内容,欢迎下载使用。
2020眉山东坡区多悦高级中学校高二上学期期中考试数学(文史类)试题扫描版含答案: 这是一份2020眉山东坡区多悦高级中学校高二上学期期中考试数学(文史类)试题扫描版含答案
2021眉山东坡区多悦高级中学高二下学期期中考试数学(理)试题含答案: 这是一份2021眉山东坡区多悦高级中学高二下学期期中考试数学(理)试题含答案












