山西省大同市第一中学校2022-2023学年九年级上学期第一次测试数学试卷(含答案)

这是一份山西省大同市第一中学校2022-2023学年九年级上学期第一次测试数学试卷(含答案)，共11页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
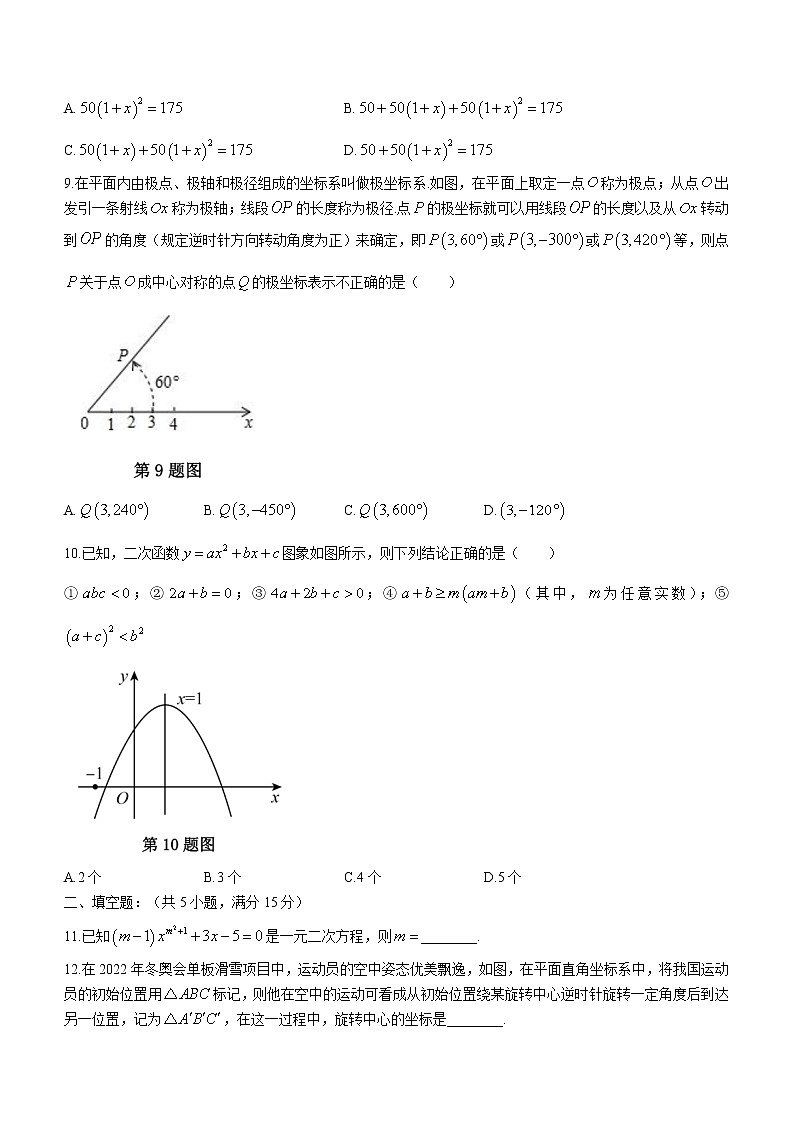
2022-2023学年度初中阶段九年级数学9月月考卷一、单选题（共10小题，共30分）1.下面的图形是用数学家名字命名的，其中是轴对称图形，但不是中心对称图形的是（    ）A. B. C. D.2.方程的根为（    ）A. B.， C. D.，3.对于二次函数，下列说法中正确的是（    ）A.图象的开口向下  B.函数的最大值为1C.图象的对称轴为直线 D.当时随的增大而减小4.在平面直角坐标系中点、关于原点对称，则点的坐标为（    ）A. B. C. D.5.若是关于的一元二次方程的一个根，则的值为（    ）A.2020 B.2022 C.2024 D.20266.在同一坐标系中，函数与的图象的大致位置可能是（    ）A. B. C. D.7.把抛物线的图象向左平移2个单位，再向上平移3个单位，所得的抛物线的函数关系式是（    ）A.  B.C.  D.8.山西省大同市经济开发区，2022年一月份工业产值达50亿元，第一季度总产值为175亿元，二月、三月平均每月的增长率是多少？若设平均每月的增长率为，根据题意，可列方程为（    ）A.  B.C. D.9.在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图，在平面上取定一点称为极点；从点出发引一条射线称为极轴；线段的长度称为极径.点的极坐标就可以用线段的长度以及从转动到的角度（规定逆时针方向转动角度为正）来确定，即或或等，则点关于点成中心对称的点的极坐标表示不正确的是（    ）A. B. C. D.10.已知，二次函数图象如图所示，则下列结论正确的是（    ）①；②；③；④（其中，为任意实数）；⑤A.2个 B.3个 C.4个 D.5个二、填空题：（共5小题，满分15分）11.已知是一元二次方程，则________.12.在2022年冬奥会单板滑雪项目中，运动员的空中姿态优美飘逸，如图，在平面直角坐标系中，将我国运动员的初始位置用标记，则他在空中的运动可看成从初始位置绕某旋转中心逆时针旋转一定角度后到达另一位置，记为，在这一过程中，旋转中心的坐标是________.13.点，，均在二次函数的图象上，则，，的大小关系是________.（用“>”连接）14.根据物理学规律，如果不考虑空气阻力，以的速度将小球沿与地面成30度角的方向击出，小球的飞行高度（单位：）与飞行时间（单位：）之间的函数关系是，当飞行时间为________时，小球达到最高点.15.如图，在直角坐标平面内，的顶点，点与点关于原点对称，，，将绕点旋转，使点落在轴上的点处，点落在点处，那么所在直线的解析式为________.三、解答题：（共8小题，满分75分）16.解方程：（共2小题，每题5分，共10分）（1）  （2）17.（共8分）阅读下列解题过程，在横线上填入适当的内容.解方程：解：移项得，①两边同除以2得，②配方得，③即∴或④∴，⑤（1）步骤②的依据是________（2分）（2）上述过程中有没有错误？若有，错在步骤________（填序号）（2分），错因是________（2分）.（3）请直接写出该方程的根（2分）18.（共7分）如图所示的正方形网格中，的顶点均在格点上，在所给直角坐标系中解答下列问题：（1）作出绕原点逆时针旋转得到的.（2分）（2）作出关于原点成中心对称的；（2分）（3）点在坐标平面上，如果以、、、为顶点的四边形是平行四边形，请直接写出点的坐标为________.（3分）19.（6分）阅读与理解：法国数学家韦达在研究一元二次方程时有一项重大发现：如果一元二次方程的两个根分别是和，那么，.例如：方程的两根分别是和，则，.请同学们阅读后利用上述结论完成下列问题：（1）（2分）已知方程的两根分别是和，则________，________.（2）（4分）已知方程的两根分别是和，求的值.20.（9分）如图，中，，.将绕点顺时针旋转得到，，交于点.（1）（5分）求证：；（2）（4分）求的度数.21.（11分）2022年在中国举办的冬奥会和残奥会世界晒目，冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓。市场上雪容融的进价比冰墩墩的进价每套便宜10元，某经销商用8000元购进的冰墩墩和用6000元购进的雪容融套数相同.在销售中，该商家发现冰墩墩每套售价50元时，每天可售出100套；每套售价提高1元时，每天少售出2套.（1）（5分）求冰墩墩和雪容融每套的进价；（2）（6分）设冰墩墩每套售价元（），表示该经销商每天销售冰墩墩的利润（单位：元），求关于的函数解析式并求最大利润.22.（12分）在正方形中，点、分别在边、上，且.（1）（4分）将绕点顺时针旋转，得到（如图1），求证：；（2）（6分）若直线与、的延长线分别交于点、（如图2），求证：.（3）（2分）将正方形改为长与宽不相等的矩形，其余条件不变（如图3），直接写出线段、、之间的数量关系.23.（12分）如图，已知抛物线的对称轴为直线，且抛物线与轴交于，两点，与轴交于点，其中，.（1）（4分）求抛物线的解析式；（2）（4分）在抛物线的对称轴上找一点，使点到点的距离与到点的距离之和最小，求出点的坐标；（3）（4分）设点为抛物线的对称轴上的一个动点，直接写出使为直角三角形的点的坐标.2022-2023学年度初中阶段九年级数学9月月考卷参考答案一、单选题（共10小题，共30分）1.B  2.D  3.D  4.B  5.C  6.B  7.C  8.B  9.B  10.D二、填空题（共5小题，共15分）11.  12.  13.  14.2  15.三、解答题（共8题，满分75分）（1），（5分） （2），（5分）17.（共8分）（1）等式的基本性质2 （2分）（2）②  （2分）等号右边漏加上4  （2分）（3）， （2分）18.（共7分）（1）∴如图，即为所求； （2分）（2）∴如图，即为所求； （2分）（3）点的坐标为或或， （3分）19.（6分）阅读与理解：（1）， （2分）（2）∵方程的两根分别是，，∴，， （3分）∴，  （4分）∴， （5分）∴；（6分）20.（9分）（1）解：由旋转可得：，，，∴即又∵，∴，在和中，，∴ （5分）（2）解：设与交于点，∵，∴，∵，，∵，∴. （9分）21.（11分）解：（1）设冰墩墩每套进价元，则雪容融每套进价元.则，解得：，经检验是方程的解.答：冰墩墩每套进价40元，雪容融每套进价30元.（5分）（2）由题意得，当时，每天可售100套.当冰墩墩每盒售元时，每天可售盒.每盒的利润为∴，配方得：∵，开口向下当时，随的增大而增大∴当时，取最大值为1750元.答：关于的函数解析式为，且最大利润为1750元.（11分）22.（12分）（1）证明：∵绕着点顺时针旋转，得到，∴，，∵，∴，在与中，，∴； （4分）（2）证明：设正方形的边长为.将绕着点顺时针旋转，得到，连接.则，.由（1）知，∴.∵，∴、、均为等腰直角三角形，∴，，，∴，∴，∴，∴，∴，∴，∵，，∴； （10分）（3） （12分）23.（12分）（1）∵点和点关于直线对称，∴把，，代入得：，解得∴抛物线的解析式为. （4分）（2）设直线解析式为与对称轴的交点为，此时的值最小.∴把、分别代入直线，得，解之得：，∴直线的解析式为.把代入直线得，∴.即当点到点的距离与到点的距离之和最小时的坐标为 （4分）（3）的坐标为或或或 （4分）