专题63 几何体的内切球-2023年高考数学优拔尖核心压轴题（选择、填空题）（新高考地区专用）

这是一份专题63 几何体的内切球-2023年高考数学优拔尖核心压轴题（选择、填空题）（新高考地区专用），共10页。
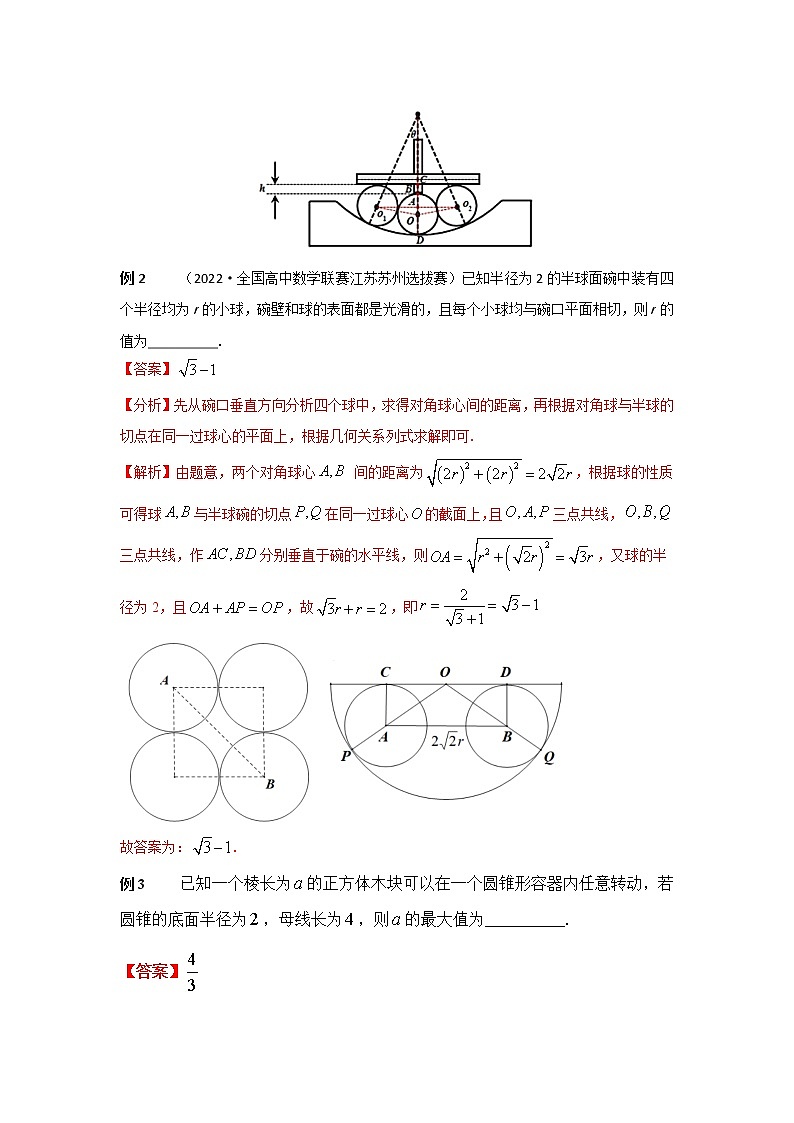
专题63 几何体的内切球【方法点拨】1.“切”的问题处理规律：(1)找准切点，通过作过球心的截面来解决．(2)体积分割是求内切球半径的常用方法．2.多面体的内切球的半径，运用“等体积法”也是常用思路.【典型题示例】例1   （2022·江苏南京、盐城·二检）某中学开展劳动实习，学生需测量某零件中圆弧的半径．如图，将三个半径为20cm的小球放在圆弧上，使它们与圆弧都相切，左、右两个小球与中间小球相切．利用“十”字尺测得小球的高度差h为8cm，则圆弧的半径为         cm． 【答案】120【解法一】由题意可知，BC＝8，AB＝12，AO＝8，设圆弧的半径为r，可得cos∠AOO1＝＝＝＝cos∠MOO1，则在△MOO1中，由余弦定理可得，(r－20)2＝(r－20)2＋402－2(r－20)40，解得r＝120．【解法二】由题意可知，BC＝8，AB＝12，AO＝8，设圆弧的半径为r，可得cos∠AOO1＝＝＝＝，即＝，解得MO＝100，则r＝MO＋20＝120．例2     （2022·全国高中数学联赛江苏苏州选拔赛）已知半径为2的半球面碗中装有四个半径均为r的小球，碗壁和球的表面都是光滑的，且每个小球均与碗口平面相切，则r的值为__________.【答案】【分析】先从碗口垂直方向分析四个球中，求得对角球心间的距离，再根据对角球与半球的切点在同一过球心的平面上，根据几何关系列式求解即可.【解析】由题意，两个对角球心 间的距离为，根据球的性质可得球与半球碗的切点在同一过球心的截面上，且三点共线，三点共线，作分别垂直于碗的水平线，则，又球的半径为2，且，故，即 故答案为：.例3   　已知一个棱长为的正方体木块可以在一个圆锥形容器内任意转动，若圆锥的底面半径为，母线长为，则的最大值为__________.【答案】【解法一】设圆锥的内切球与切于点，内切球球心为，连接，，设内切球半径为，由，的最大值为.    【解法二】设圆锥内切球半径为，正方体外接球半径为，，.的最大值为.例4    已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为________．【答案】　π【解析】　易知半径最大的球即为该圆锥的内切球．圆锥及其内切球O如图所示，    设内切球的半径为R，则sin ∠BPE＝＝＝，所以OP＝3R，所以PE＝4R＝＝＝2，所以R＝，所以内切球的体积V＝πR3＝π，即该圆锥内半径最大的球的体积为π.例5     正四面体的棱长为，是棱的中点，以为球心的球面与平面的交线和相切，则球的体积是（    ）A.  B.  C.       D. 【答案】D【分析】设点在平面内的射影为点，则为的中心，取的中点，连接，则，取线段的中点，连接，分析可知以为球心的球面与平面的交线和相切的切点为，求出，即为球的半径，再利用球体的体积公式可求得结果.【解析】设点在平面内的射影为点，则为的中心，取的中点，连接，则，取线段的中点，连接，因为、分别为、的中点，则且，因为平面，则平面，因为平面，则，正的外接圆半径为，，所以，，易知球被平面所截的截面圆圆心为点，且，故，因为为等边三角形，为的中点，则，因为以为球心的球面与平面的交线和相切，则切点为点，则球的半径为，因此，球的体积是.故选：D.             【巩固训练】1．在四棱锥P ­ABCD中，底面ABCD是边长为2a的正方形，PD⊥底面ABCD，且PD＝2a.若在这个四棱锥内放一球，则此球的最大半径为________．2.在棱长为 1的正方体内容纳 9个等球，8个角各放 1个， 中间放 1个，则这些等球的最大半径为              ．3.已知一个平放的各棱长为4的三棱锥内有一个小球O(重量忽略不计)，现从该三棱锥顶端向内注水，小球慢慢上浮，若注入的水的体积是该三棱锥体积的时，小球与该三棱锥的各侧面均相切(与水面也相切)，则小球的表面积等于(　　)A.   B.   C.   D.4.半径为R的球内部装有四个相同半径r的小球，则r的最大值为（     ）.        B.             C.            D. 5.如图，在底面边长为，高为的正四棱柱中，大球与该正四棱柱的五个面均相切，小球在大球上方且与该正四棱柱的三个面相切，也与大球相切，则小球的半径为___________．    6.球O与棱长为2的正方体的各个面都相切，点M为棱的中点，则平面ACM截球O所得的截面圆与球心O所构成的圆锥的体积为______．7.我国古代数学名著《九章算术》中将正四棱锥称为方锥.已知某方锥各棱长均为2，则其内切球的体积为______.8.正三棱柱有一个半径为的内切球，则此棱柱的体积是（    ）.A． B． C． D． 【答案或提示】1.【答案】(2－)a【解析】由题意知，当球与四棱锥各面均相切，即内切于四棱锥时球的半径最大．作出过球心的截面图，如图所示．易知球的半径r＝(2－)a.  2.【答案】【解析】当球半径最大时，8个角上的球必与正方体的三个面相切，切点在各面的对角线上，球心都在正方体的体对角面上作轴截面，设球半径为，则，而故.       3.【答案】　C【解析】　当注入水的体积是该三棱锥体积的时，设水面上方的小三棱锥的棱长为x(各棱长都相等).依题意，＝，得x＝2，易得小三棱锥的高为.设小球半径为r，则S底面·＝4×S底面·r(S底面为小三棱锥的底面积)，得r＝.故小球的表面积S＝4πr2＝.4.【答案】B5.【答案】.【分析】设出小球半径，结合图形，利用已知条件，根据勾股定理，即可求出答案.【解析】易知大球的半径为 ，设小球的半径为，为小球球心，为大球球心，大球与正四棱柱的下底面相切与点，小球与正四棱柱的上底面相切与点，连接，作 于点，如图，由题意可知，,，所以，, 因为两圆相切，所以 ，因为为直角三角形，所以，即 ， 又因为 ，所以 .故答案为：.     6.【答案】【分析】由球心O为正方体的中心，连接BD与AC交于点F，作，易知 OE为所得圆锥的高，底面的半径为求解.【解析】如图所示：易知球心O为正方体的中心，连接BD与AC交于点F，作，易知面，则，又,所以平面，则OE为所得圆锥的高，又，圆锥的底面的半径为，所以圆锥的体积为，故答案为：.7.【答案】【解析】如图，设方锥底面的中心为，则在中，，所以，在中，，所以方锥的体积为，设方锥内切球的半径为，而方锥的表面积为，由等体积法可得，解得，体积为.故填：.    8.【答案】B【解析】∵正三棱柱有一个半径为的内切球，则正三棱柱的高为cm，底面正三角形的内切圆的半径为cm，设底面正三角形的边长为cm,则，解得cm，∴正三棱柱的底面面积为cm2，故此正三棱柱的体积V＝cm3．故选：B．