广东省广州市番禺区重点名校2022年中考数学押题试卷含解析

这是一份广东省广州市番禺区重点名校2022年中考数学押题试卷含解析，共23页。试卷主要包含了答题时请按要求用笔等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
注意事项:
1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1．如图，已知的周长等于 ，则它的内接正六边形ABCDEF的面积是（ ）

A． B． C． D．
2．如图，直线a∥b，直线c与直线a、b分别交于点A、点B，AC⊥AB于点A，交直线b于点C．如果∠1=34°，那么∠2的度数为（ ）

A．34° B．56° C．66° D．146°
3．下列图形中，既是中心对称图形，又是轴对称图形的是（ ）
A． B． C． D．
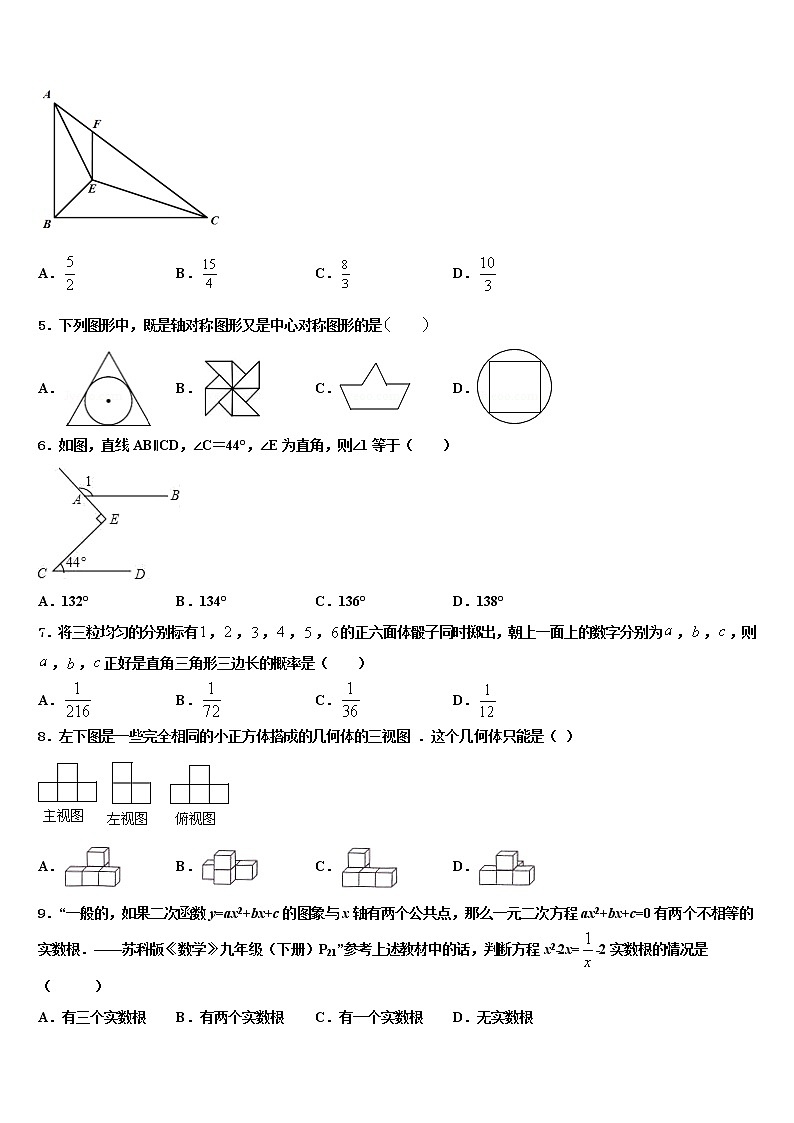
4．如图，在Rt△ABC中，∠ABC=90°，AB=6，BC=8，点E是△ABC的内心，过点E作EF∥AB交AC于点F，则EF的长为( )

A． B． C． D．
5．下列图形中，既是轴对称图形又是中心对称图形的是　　
A． B． C． D．
6．如图，直线AB∥CD，∠C＝44°，∠E为直角，则∠1等于（　　）

A．132° B．134° C．136° D．138°
7．将三粒均匀的分别标有，，，，，的正六面体骰子同时掷出，朝上一面上的数字分别为，，，则，，正好是直角三角形三边长的概率是（　　）
A． B． C． D．
8．左下图是一些完全相同的小正方体搭成的几何体的三视图 ．这个几何体只能是（ ）

A． B． C． D．
9．“一般的，如果二次函数y=ax2+bx+c的图象与x轴有两个公共点，那么一元二次方程ax2+bx+c=0有两个不相等的实数根．——苏科版《数学》九年级（下册）P21”参考上述教材中的话，判断方程x2﹣2x=﹣2实数根的情况是 （ ）
A．有三个实数根 B．有两个实数根 C．有一个实数根 D．无实数根
10．如图，已知双曲线经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为（，4），则△AOC的面积为

A．12 B．9 C．6 D．4
11．某小组在“用频率估计概率”的试验中，统计了某种结果出现的频率，绘制了如图所示的折线图，那么符合这一结果的试验最有可能的是（　　）

A．在装有1个红球和2个白球（除颜色外完全相同）的不透明袋子里随机摸出一个球是“白球”
B．从一副扑克牌中任意抽取一张，这张牌是“红色的”
C．掷一枚质地均匀的硬币，落地时结果是“正面朝上”
D．掷一个质地均匀的正六面体骰子，落地时面朝上的点数是6
12．我国第一艘航母“辽宁舰”最大排水量为67500吨，用科学记数法表示这个数字是
A．6.75×103吨 B．67.5×103吨 C．6.75×104吨 D．6.75×105吨
二、填空题：（本大题共6个小题，每小题4分，共24分．）
13．我们知道：四边形具有不稳定性.如图，在平面直角坐标系xOy中，矩形ABCD的边AB在x轴上，，，边AD长为5. 现固定边AB，“推”矩形使点D落在y轴的正半轴上（落点记为），相应地，点C的对应点的坐标为_______.

14．如图，与是以点为位似中心的位似图形，相似比为，，，若点的坐标是，则点的坐标是__________．

15．正多边形的一个外角是60°，边长是2，则这个正多边形的面积为___________ .
16．如果分式的值为0，那么x的值为___________．
17． “若实数a，b，c满足a＜b＜c，则a+b＜c”，能够说明该命题是假命题的一组a，b，c的值依次为_____．
18．已知x1，x2是方程x2-3x-1=0的两根，则=______．
三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19．（6分）M中学为创建园林学校，购买了若干桂花树苗，计划把迎宾大道的一侧全部栽上桂花树（两端必须各栽一棵），并且每两棵树的间隔相等，如果每隔5米栽1棵，则树苗缺11棵；如果每隔6米栽1棵，则树苗正好用完，求购买了桂花树苗多少棵？
20．（6分）如图，在平面直角坐标系中，已知△AOB是等边三角形，点A的坐标是（0，4），点B在一象限，点P（t，0）是x轴上的一个动点，连接AP，并把△AOP绕着点A按逆时针方向旋转，使边AO与AB重合，连接OD，PD，得△OPD。

（1）当t＝时，求DP的长
（2）在点P运动过程中，依照条件所形成的△OPD面积为S
①当t＞0时，求S与t之间的函数关系式
②当t≤0时，要使s＝，请直接写出所有符合条件的点P的坐标.
21．（6分）徐州至北京的高铁里程约为700km，甲、乙两人从徐州出发，分别乘坐“徐州号”高铁A与“复兴号”高铁B前往北京．已知A车的平均速度比B车的平均速度慢80km/h，A车的行驶时间比B车的行驶时间多40%，两车的行驶时间分别为多少？
22．（8分）已知Rt△ABC中，∠ACB＝90°，CA＝CB＝4，另有一块等腰直角三角板的直角顶点放在C处，CP＝CQ＝2，将三角板CPQ绕点C旋转(保持点P在△ABC内部)，连接AP、BP、BQ．如图1求证：AP＝BQ；如图2当三角板CPQ绕点C旋转到点A、P、Q在同一直线时，求AP的长；设射线AP与射线BQ相交于点E，连接EC，写出旋转过程中EP、EQ、EC之间的数量关系．

23．（8分）如图，△ABC中，CD是边AB上的高，且．
求证：△ACD∽△CBD；求∠ACB的大小．
24．（10分）如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.

25．（10分）已知：二次函数C1：y1＝ax2+2ax+a﹣1(a≠0)把二次函数C1的表达式化成y＝a(x﹣h)2+b(a≠0)的形式，并写出顶点坐标；已知二次函数C1的图象经过点A(﹣3，1)．
①求a的值；
②点B在二次函数C1的图象上，点A，B关于对称轴对称，连接AB．二次函数C2：y2＝kx2+kx(k≠0)的图象，与线段AB只有一个交点，求k的取值范围．

26．（12分）如图，在等边△ABC中，点D是 AB边上一点，连接CD，将线段CD绕点C按顺时针方向旋转60°后得到CE，连接AE．求证：AE∥BC．

27．（12分）如图，点B、E、C、F在同一条直线上，AB＝DE，AC＝DF，BE＝CF，求证：AB∥DE．




参考答案

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1、C
【解析】
过点O作OH⊥AB于点H，连接OA，OB，由⊙O的周长等于6πcm，可得⊙O的半径，又由圆的内接多边形的性质可得∠AOB=60°，即可证明△AOB是等边三角形，根据等边三角形的性质可求出OH的长，根据S正六边形ABCDEF=6S△OAB即可得出答案．
【详解】
过点O作OH⊥AB于点H，连接OA，OB，设⊙O的半径为r，
∵⊙O的周长等于6πcm，
∴2πr=6π，
解得：r=3，
∴⊙O的半径为3cm，即OA=3cm，
∵六边形ABCDEF是正六边形，
∴∠AOB=×360°=60°，OA=OB，
∴△OAB是等边三角形，
∴AB=OA=3cm，
∵OH⊥AB，
∴AH=AB，
∴AB=OA=3cm，
∴AH=cm，OH==cm，
∴S正六边形ABCDEF=6S△OAB=6××3×=（cm2）．

故选C.
【点睛】
此题考查了正多边形与圆的性质．此题难度适中，注意掌握数形结合思想的应用．
2、B
【解析】
分析：先根据平行线的性质得出∠2+∠BAD=180°，再根据垂直的定义求出∠2的度数．
详解：∵直线a∥b，∴∠2+∠BAD=180°．
∵AC⊥AB于点A，∠1=34°，∴∠2=180°﹣90°﹣34°=56°．
故选B．

点睛：本题主要考查了平行线的性质，解题的关键是掌握两直线平行，同旁内角互补，此题难度不大．
3、C
【解析】
根据中心对称图形和轴对称图形对各选项分析判断即可得解．
【详解】
A、不是轴对称图形，是中心对称图形，故本选项错误；
B、不是中心对称图形，是轴对称图形，故本选项错误；
C、既是中心对称图形，又是轴对称图形，故本选项正确；
D、是轴对称图形，不是中心对称图形，故本选项错误．
故选C．
【点睛】
本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．
4、A
【解析】
过E作EG∥AB，交AC于G，易得CG=EG，EF=AF，依据△ABC∽△GEF，即可得到EG：EF：GF，根据斜边的长列方程即可得到结论．
【详解】
过E作EG∥BC，交AC于G，则∠BCE=∠CEG．
∵CE平分∠BCA，∴∠BCE=∠ACE，∴∠ACE=∠CEG，∴CG=EG，同理可得：EF=AF．
∵BC∥GE，AB∥EF，∴∠BCA=∠EGF，∠BAC=∠EFG，∴△ABC∽△GEF．
∵∠ABC=90°，AB=6，BC=8，∴AC=10，∴EG：EF：GF=BC：BC：AC=4：3：5，设EG=4k=AG，则EF=3k=CF，FG=5k．
∵AC=10，∴3k+5k+4k=10，∴k=，∴EF=3k=．
故选A．

【点睛】
本题考查了相似三角形的判定与性质，等腰三角形的性质以及勾股定理的综合运用，解决问题的关键是作辅助线构相似三角形以及构造等腰三角形．
5、D
【解析】
根据轴对称图形和中心对称图形的定义逐项识别即可，在平面内，把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形；如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形.
【详解】
解：A. 是轴对称图形，但不是中心对称图形，故不符合题意；
B. 不是轴对称图形，是中心对称图形，故不符合题意；
C. 是轴对称图形，但不是中心对称图形，故不符合题意；
D. 既是轴对称图形又是中心对称图形，故符合题意．
故选D.
【点睛】
本题考查了轴对称图形和中心对称图形的识别，熟练掌握轴对称图形和中心对称图形的定义是解答本题的关键.
6、B
【解析】
过E作EF∥AB，求出AB∥CD∥EF，根据平行线的性质得出∠C=∠FEC，∠BAE=∠FEA，求出∠BAE，即可求出答案．
解：

过E作EF∥AB，
∵AB∥CD，
∴AB∥CD∥EF，
∴∠C=∠FEC，∠BAE=∠FEA，
∵∠C=44°，∠AEC为直角，
∴∠FEC=44°，∠BAE=∠AEF=90°﹣44°=46°，
∴∠1=180°﹣∠BAE=180°﹣46°=134°，
故选B．
“点睛”本题考查了平行线的性质的应用，能正确作出辅助线是解此题的关键．
7、C
【解析】
三粒均匀的正六面体骰子同时掷出共出现216种情况,而边长能构成直角三角形的数字为3、4、5,含这三个数字的情况有6种,故由概率公式计算即可.
【详解】
解:因为将三粒均匀的分别标有1,2,3,4,5,6的正六面体骰子同时掷出,按出现数字的不同共=216种情况,其中数字分别为3,4,5,是直角三角形三边长时,有6种情况,所以其概率为,
故选C.
【点睛】
本题考查的是概率的求法.如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.边长为3,4,5的三角形组成直角三角形.
8、A
【解析】
试题分析：根据几何体的主视图可判断C不合题意；根据左视图可得B、D不合题意，因此选项A正确，故选A．
考点：几何体的三视图
9、C
【解析】
试题分析：由得，，即是判断函数与函数的图象的交点情况.



因为函数与函数的图象只有一个交点
所以方程只有一个实数根
故选C.
考点：函数的图象
点评：函数的图象问题是初中数学的重点和难点，是中考常见题，在压轴题中比较常见，要特别注意.
10、B
【解析】
∵点，是中点
∴点坐标
∵在双曲线上，代入可得
∴
∵点在直角边上，而直线边与轴垂直
∴点的横坐标为-6
又∵点在双曲线
∴点坐标为
∴
从而，故选B
11、D
【解析】
根据统计图可知，试验结果在0.16附近波动，即其概率P≈0.16，计算四个选项的概率，约为0.16者即为正确答案．
【详解】
根据图中信息，某种结果出现的频率约为0.16，
在装有1个红球和2个白球（除颜色外完全相同）的不透明袋子里随机摸出一个球是“白球”的概率为≈0.67>0.16，故A选项不符合题意，
从一副扑克牌中任意抽取一张，这张牌是“红色的”概率为≈0.48>0.16，故B选项不符合题意，
掷一枚质地均匀的硬币，落地时结果是“正面朝上”的概率是=0.5>0.16，故C选项不符合题意，
掷一个质地均匀的正六面体骰子，落地时面朝上的点数是6的概率是≈0.16，故D选项符合题意，
故选D.
【点睛】
本题考查了利用频率估计概率，大量反复试验下频率稳定值即概率．用到的知识点为：频率=所求情况数与总情况数之比．熟练掌握概率公式是解题关键.
12、C
【解析】
试题分析：根据科学记数法的定义，科学记数法的表示形式为a×10n，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．在确定n的值时，看该数是大于或等于1还是小于1．当该数大于或等于1时，n为它的整数位数减1；当该数小于1时，－n为它第一个有效数字前0的个数（含小数点前的1个0）．67500一共5位，从而67 500=6.75×2．故选C．

二、填空题：（本大题共6个小题，每小题4分，共24分．）
13、
【解析】
分析：根据勾股定理，可得 ,根据平行四边形的性质，可得答案.
详解：由勾股定理得：= ,即(0,4).
矩形ABCD的边AB在x轴上，∴四边形是平行四边形，
A=B, =AB=4-(-3)=7, 与的纵坐标相等，∴（7,4），故答案为（7,4）.
点睛：本题考查了多边形，利用平行四边形的性质得出A=B,=AB=4-(-3)=7是解题的关键.
14、（2，2）
【解析】
分析：首先解直角三角形得出A点坐标，再利用位似是特殊的相似，若两个图形与是以点为位似中心的位似图形，相似比是k，上一点的坐标是 则在中，它的对应点的坐标是或，进而求出即可．
详解：与是以点为位似中心的位似图形，，

，若点的坐标是，

过点作交于点E.

点的坐标为：
与的相似比为，
点的坐标为：即点的坐标为：
故答案为：

点睛：考查位似图形的性质，熟练掌握位似图形的性质是解题的关键.
15、6
【解析】
多边形的外角和等于360°，因为所给多边形的每个外角均相等，据此即可求得正多边形的边数，进而求解．
【详解】
正多边形的边数是：360°÷60°=6.
正六边形的边长为2cm，
由于正六边形可分成六个全等的等边三角形，
且等边三角形的边长与正六边形的边长相等，
所以正六边形的面积.
故答案是：.
【点睛】
本题考查了正多边形的外角和以及正多边形的计算，正六边形可分成六个全等的等边三角形，转化为等边三角形的计算.
16、4
【解析】
∵，
∴x-4=0，x+2≠0，
解得：x=4，
故答案为4.
17、答案不唯一，如1,2,3；
【解析】
分析：设a，b，c是任意实数．若a 详解：设a，b，c是任意实数．若a 则若a 可设a，b，c的值依次1，2，3，（答案不唯一），
故答案为1，2，3.
点睛：本题考查了命题的真假，举例说明即可，
18、﹣1．
【解析】
试题解析：∵，是方程的两根，∴、，∴== =﹣1．故答案为﹣1．

三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19、购买了桂花树苗1棵
【解析】
分析：首先设购买了桂花树苗x棵，然后根据题意列出一元一次方程，从而得出答案．
详解：设购买了桂花树苗x棵，根据题意，得：5(x+11-1)=6(x-1)， 解得x=1．
答：购买了桂花树苗1棵．
点睛：本题主要考查的是一元一次方程的应用，属于基础题型．解决这个问题的关键就是找出等量关系以及路的长度与树的棵树之间的关系．
20、（1）DP=；（2）①；②.
【解析】
（1）先判断出△ADP是等边三角形，进而得出DP=AP，即可得出结论；
（2）①先求出GH= 2，进而求出DG，再得出DH，即可得出结论；
②分两种情况，利用三角形的面积建立方程求解即可得出结论．
【详解】
解：（1）∵A（0，4），
∴OA=4，
∵P（t，0），
∴OP=t，
∵△ABD是由△AOP旋转得到，
∴△ABD≌△AOP，
∴AP=AD，∠DAB=∠PAO，
∴∠DAP=∠BAO=60°，
∴△ADP是等边三角形，
∴DP=AP，
∵ ，
∴，
∴；
（2）①当t＞0时，如图1，BD=OP=t，

过点B，D分别作x轴的垂线，垂足于F，H，过点B作x轴的平行线，分别交y轴于点E，交DH于点G，
∵△OAB为等边三角形，BE⊥y轴，
∴∠ABP=30°，AP=OP=2，
∵∠ABD=90°，
∴∠DBG=60°，
∴DG=BD•sin60°= ，
∵GH=OE=2，
∴ ，
∴ ；
②当t≤0时，分两种情况：
∵点D在x轴上时，如图2

在Rt△ABD中，，
(1)当 时，如图3，BD=OP=-t，，

∴，
∴，
∴或，
∴ 或，
（2）当 时，如图4，

BD=OP=-t，，
∴，
∴
∴或（舍）
∴ ．
【点睛】
此题是几何变换综合题，主要考查了全等三角形的判定和性质，旋转的性质，三角形的面积公式以及解直角三角形，正确作出辅助线是解决本题的关键．
21、A车行驶的时间为3.1小时，B车行驶的时间为2.1小时．
【解析】
设B车行驶的时间为t小时，则A车行驶的时间为1.4t小时，根据题意得：﹣=80，解分式方程即可，注意验根.
【详解】
解：设B车行驶的时间为t小时，则A车行驶的时间为1.4t小时，
根据题意得：﹣=80，
解得：t=2.1，
经检验，t=2.1是原分式方程的解，且符合题意，
∴1.4t=3.1．
答：A车行驶的时间为3.1小时，B车行驶的时间为2.1小时．
【点睛】
本题考核知识点：列分式方程解应用题.解题关键点：根据题意找出数量关系，列出方程.
22、（1）证明见解析（2） （3）EP+EQ= EC
【解析】
（1）由题意可得：∠ACP=∠BCQ，即可证△ACP≌△BCQ，可得 AP=CQ；
作 CH⊥PQ 于 H，由题意可求 PQ=2 ，可得 CH=，根据勾股定理可求
AH= ，即可求 AP 的长；
作 CM⊥BQ 于 M，CN⊥EP 于 N，设 BC 交 AE 于 O，由题意可证△CNP≌△ CMQ，可得 CN=CM，QM=PN，即可证 Rt△CEM≌Rt△CEN，EN=EM，∠CEM=
∠CEN=45°，则可求得 EP、EQ、EC 之间的数量关系．
【详解】
解：（1）如图 1 中，∵∠ACB=∠PCQ=90°，
∴∠ACP=∠BCQ 且 AC=BC，CP=CQ
∴△ACP≌△BCQ（SAS）
∴PA=BQ
如图 2 中，作 CH⊥PQ 于 H
∵A、P、Q 共线，PC=2，
∴PQ=2，
∵PC=CQ，CH⊥PQ
∴CH=PH=
在 Rt△ACH 中，AH==
∴PA=AH﹣PH= -
解：结论：EP+EQ= EC
理由：如图 3 中，作 CM⊥BQ 于 M，CN⊥EP 于 N，设 BC 交 AE 于 O．

∵△ACP≌△BCQ，
∴∠CAO=∠OBE，
∵∠AOC=∠BOE，
∴∠OEB=∠ACO=90°，
∵∠M=∠CNE=∠MEN=90°，
∴∠MCN=∠PCQ=90°，
∴∠PCN=∠QCM，
∵PC=CQ，∠CNP=∠M=90°，
∴△CNP≌△CMQ（AAS），
∴CN=CM，QM=PN，
∴CE=CE，
∴Rt△CEM≌Rt△CEN（HL），
∴EN=EM，∠CEM=∠CEN=45°
∴EP+EQ=EN+PN+EM﹣MQ=2EN，EC=EN，
∴EP+EQ=EC
【点睛】
本题考查几何变换综合题，解答关键是等腰直角三角形的性质，全等三角形的性质和判定，添加恰当辅助线构造全等三角形．
23、（1）证明见试题解析；（2）90°．
【解析】
试题分析：（1）由两边对应成比例且夹角相等的两个三角形相似，即可证明△ACD∽△CBD；
（2）由（1）知△ACD∽△CBD，然后根据相似三角形的对应角相等可得：∠A=∠BCD，然后由∠A+∠ACD=90°，可得：∠BCD+∠ACD=90°，即∠ACB=90°．
试题解析：（1）∵CD是边AB上的高，
∴∠ADC=∠CDB=90°，
∵．
∴△ACD∽△CBD；
（2）∵△ACD∽△CBD，
∴∠A=∠BCD，
在△ACD中，∠ADC=90°，
∴∠A+∠ACD=90°，
∴∠BCD+∠ACD=90°，
即∠ACB=90°．
考点：相似三角形的判定与性质．
24、50°.
【解析】
试题分析：由平行线的性质得到∠ABC=∠1=65°，∠ABD+∠BDE=180°，由BC平分∠ABD，得到∠ABD=2∠ABC=130°，于是得到结论．
解：∵AB∥CD，
∴∠ABC=∠1=65°，
∵BC平分∠ABD，
∴∠ABD=2∠ABC=130°，
∴∠BDE=180°﹣∠ABD=50°，
∴∠2=∠BDE=50°．

【点评】
本题考查了平行线的性质和角平分线定义等知识点，解此题的关键是求出∠ABD的度数，题目较好，难度不大．
25、 (1)y1＝a(x+1)2﹣1，顶点为(﹣1，﹣1)；(2)①；②k的取值范围是≤k≤或k＝﹣1．
【解析】
(1)化成顶点式即可求得；
(2)①把点A(﹣3，1)代入二次函数C1：y1＝ax2+2ax+a﹣1即可求得a的值；
②根据对称的性质得出B的坐标，然后分两种情况讨论即可求得；
【详解】
(1)y1＝ax2+2ax+a﹣1＝a(x+1)2﹣1，
∴顶点为(﹣1，﹣1)；
(2)①∵二次函数C1的图象经过点A(﹣3，1)，
∴a(﹣3+1)2﹣1＝1，
∴a＝；
②∵A(﹣3，1)，对称轴为直线x＝﹣1，
∴B(1，1)，
当k＞0时，
二次函数C2：y2＝kx2+kx(k≠0)的图象经过A(﹣3，1)时，1＝9k﹣3k，解得k＝，
二次函数C2：y2＝kx2+kx(k≠0)的图象经过B(1，1)时，1＝k+k，解得k＝，
∴≤k≤，
当k＜0时，∵二次函数C2：y2＝kx2+kx＝k(x+)2﹣k，
∴﹣k＝1，
∴k＝﹣1，
综上，二次函数C2：y2＝kx2+kx(k≠0)的图象，与线段AB只有一个交点，k的取值范围是≤k≤或k＝﹣1．
【点睛】
本题考查了二次函数和系数的关系，二次函数的最值问题，轴对称的性质等，分类讨论是解题的关键．
26、见解析
【解析】
试题分析:根据等边三角形的性质得出AC=BC,∠B=∠ACB=60°,根据旋转的性质得出CD=CE,∠DCE=60°,求出∠BCD=∠ACE,根据SAS推出△BCD≌△ACE,根据全等得出∠EAC=∠B=60°,求出∠EAC=∠ACB,根据平行线的判定得出即可.
试题解析:∵△ABC是等边三角形,
∴AC=BC,∠B=∠ACB=60°,
∵线段CD绕点C顺时针旋转60°得到CE,
∴CD=CE,∠DCE=60°,
∴∠DCE=∠ACB,即∠BCD+∠DCA=∠DCA+∠ACE,
∴∠BCD=∠ACE,
在△BCD与△ACE中,
,
∴△BCD≌△ACE,
∴∠EAC=∠B=60°,
∴∠EAC=∠ACB,
∴AE∥BC.
27、详见解析.
【解析】
试题分析：利用SSS证明△ABC≌△DEF，根据全等三角形的性质可得∠B=∠DEF，再由平行线的判定即可得AB∥DE．
试题解析：证明：由BE＝CF可得BC＝EF，
又AB＝DE，AC＝DF，
故△ABC≌△DEF（SSS），
则∠B=∠DEF，
∴AB∥DE．
考点：全等三角形的判定与性质.