



2022-2023年高考物理一轮复习 带电粒子在磁场中的运动——磁聚焦 课件
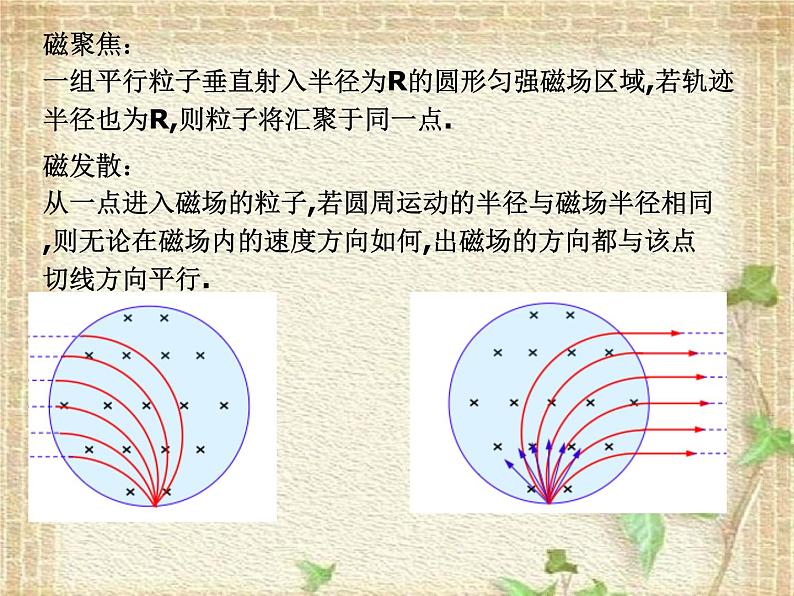
展开磁聚焦:一组平行粒子垂直射入半径为R的圆形匀强磁场区域,若轨迹半径也为R,则粒子将汇聚于同一点.
磁发散:从一点进入磁场的粒子,若圆周运动的半径与磁场半径相同,则无论在磁场内的速度方向如何,出磁场的方向都与该点切线方向平行.
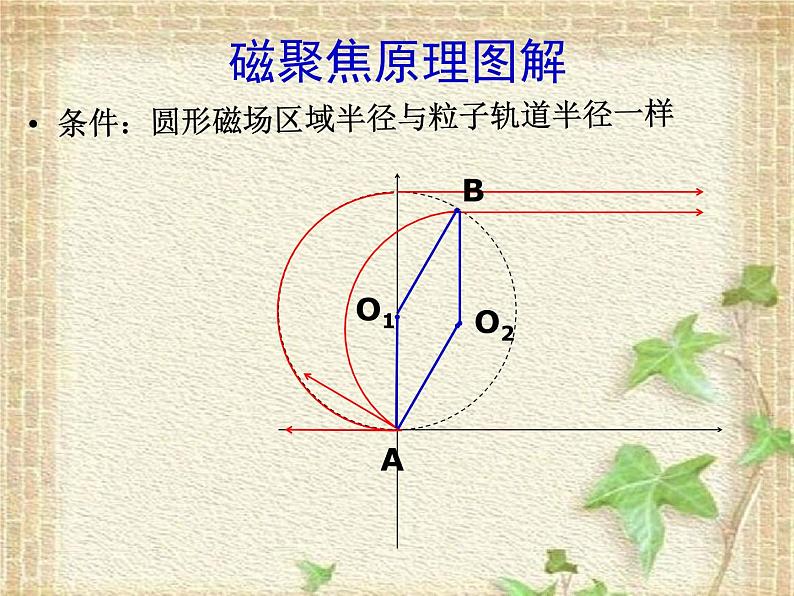
条件:圆形磁场区域半径与粒子轨道半径一样
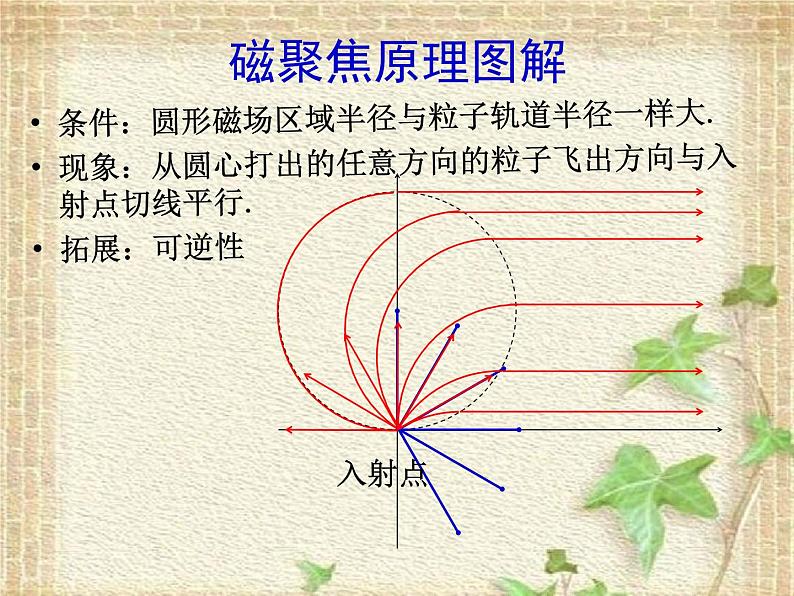
条件:圆形磁场区域半径与粒子轨道半径一样大.现象:从圆心打出的任意方向的粒子飞出方向与入射点切线平行.拓展:可逆性
例1:如右图所示,在半径为R的圆形区域内充满磁感应强度为B的匀强磁场,MN是一竖直放置的感光板.从圆形磁场最高点P垂直磁场射入大量的带正电、电荷量为q、质量为m、速度为v的粒子,不考虑粒子间的相互作用力,关于这些粒子的运动以下说法正确的是( )A.只要对着圆心入射,出射后均可垂直打在MN上B.对着圆心入射的粒子,其出射方向的反向延长线不一定过圆心C.对着圆心入射的粒子,速度越大在磁场中通过的弧长越长,时间也越长D.只要速度满足 ,沿不同方向入射的粒子出射后均可垂直打在MN上
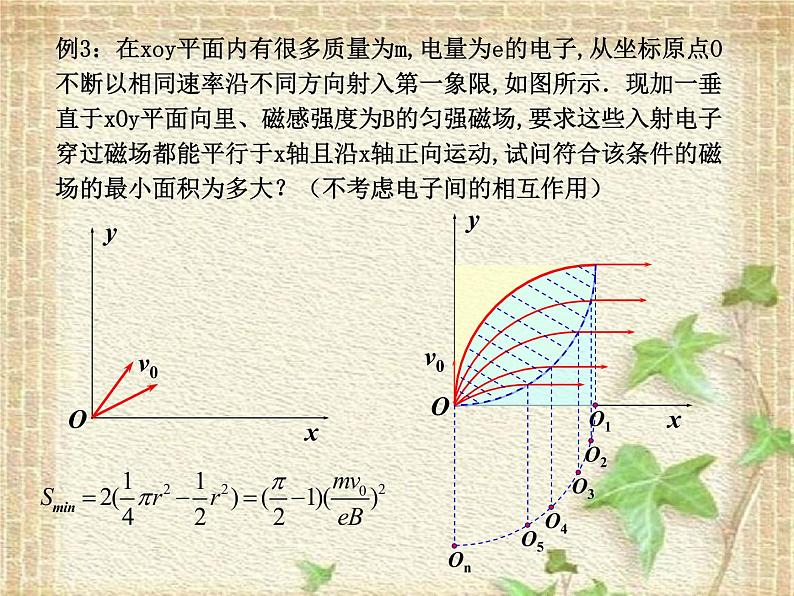
例3:在xy平面内有很多质量为m,电量为e的电子,从坐标原点O不断以相同速率沿不同方向射入第一象限,如图所示.现加一垂直于xOy平面向里、磁感强度为B的匀强磁场,要求这些入射电子穿过磁场都能平行于x轴且沿x轴正向运动,试问符合该条件的磁场的最小面积为多大?(不考虑电子间的相互作用)
例4:电子质量为m、电量为e,从坐标原点O处沿xOy平面射入第一象限,射入时速度方向不同,速度大小均为v0,如图所示.现在某一区域加方向向外且垂直于xOy平面的匀强磁场,磁感应强度为B,若这些电子穿过磁场后都能垂直射到荧光屏MN上,荧光屏与y轴平行,求:(1)电子在磁场中的运动半径大小;(2)荧光屏上光斑的长度;(3)所加磁场范围的最小面积.
(1)mv0/eB(2)mv0/eB(3)(π/2+1)(mv0/eB)2
例3:如图,ABCD是边长为a的正方形.质量为m电荷量为e的电子以大小为v0的初速度沿纸面垂直于BC边射入正方形区域.在正方形内适当区域中有匀强磁场,电子从BC边上的任意点入射,都只能从A点射出磁场.不计重力,求:(1)此匀强磁场区域中磁感应强度的大小和方向;(2)此匀强磁场区域的最小面积.
S=2(πa2/4-a2/2) =(π-2)a2/2
解:(1)设匀强磁场的磁感应强度的大小为B.令圆弧AEC是自C点垂直于BC入射的电子在磁场中的运行轨道.依题意,圆心在A、C连线的中垂线上,故B点即为圆心,圆半径为a,按照牛顿定律有 ev0B= mv02/a,得B= mv0/ea.
(2)自BC边上其他点入射的电子运动轨道只能在BAEC区域中.因而,圆弧AEC是所求的最小磁场区域的一个边界.
(3)设某射中A点的电子速度方向与BA的延长线夹角为θ的情形.该电子的运动轨迹qpA如图所示.图中圆弧Ap的圆心为O,pq垂直于BC边 ,圆弧Ap的半径仍为a,在D为原点、DC为x轴、DA为y轴的坐标系中,p点的坐标为(x,y),则 x=asinθ,y=-acsθ.
因此,所求的最小匀强磁场区域,是分别以B和D为圆心、a为半径的两个四分之一圆周AEC和AFC所围成的区域,其面积为S=2(πa2/4-a2/2) =(π-2)a2/2
由④⑤式可得:x2+y2=a2,这意味着在范围0≤θ≤π/2内,p点处在以D为圆心、a为半径的四分之一圆周AFC上,它是电子做直线运动和圆周运动的分界线,构成所求磁场区域的另一边界.
区域半径 R 与运动半径 r 相等
迁移与逆向、对称的物理思想!
例、如图,在xOy平面内与y轴平行的匀强电场,在半径为R的圆内还有与xOy平面垂直的匀强磁场.在圆的左边放置一带电微粒发射装置,它沿x轴正方向发射出一束具有相同质量m、电荷量q(q>0)和初速度v的带电微粒.发射时,这束带电微粒分布在0<y<2R的区间内.已知重力加速度大小为g.(1)从A点射出的带电微粒平行于x轴从C点进入有磁场区域,并从坐标原点O沿y轴负方向离开,求电场强度和磁感应强度的大小与方向.(2)请指出这束带电微粒与x轴相 交的区域,并说明理由.(3)在这束带电磁微粒初速度变为 2v,那么它们与x轴相交的区域又在 哪里?并说明理由.
【答案】(1);方向垂直于纸面向外(2)见解析(3)与x同相交的区域范围是x>0.
例、如图,在xOy平面内,有以O′(R,0)为圆心,R为半径的圆形磁场区域,磁感应强度大小为 B,方向垂直xOy平面向外,在 y=R上方有范围足够大的匀强电场,方向水平向右,电场强度大小为E.在坐标原点O处有一放射源,可以在xOy平面内向 y 轴右侧(x >0)发射出速率相同的电子,已知电子在该磁场中的偏转半径也为 R, 电子电量为 e,质量为 m. 不计重力及阻力的作用. (1)求电子射入磁场时的速度大小; (2)速度方向沿x轴正方向射入磁场 的电子,求它到达y轴所需要的时间; (3)求电子能够射到y轴上的范围.
例、如图所示,在 xOy平面上-H < y< H的范围内有一片稀疏的电子,从 x 轴的负半轴的远外以相同的速率 v0 沿 x 轴正向平行地向 y 轴射来,试设计一个磁场区域,使得:(1)所有电子都能在磁场力作用下通过原点 O; (2)这一片电子最后扩展到 -2H
(1)如图所示,设沿CM方向运动的离子在磁场中做圆周运动的轨道半径为R,
由R=d ,qv0B = mv02/R
可得 B=mv0/qd,磁场方向垂直纸面向外.
(2)设沿CN运动的离子速度大小为v,在磁场中的轨道半径为R′,运动时间为t由 vcsθ = v0, 得v = v0/csθ.
R′=mv/qB = d/csθ.
设弧长为s,t=s/v,s=2(θ+α) R′
离子在磁场中做匀速圆周运动的周期T= 2π m /Bq,
(3) CM=MNctθ
以上3式联立求解得 CM=d ctα
例、如图,在直角坐标系 xOy 中,点M(0,1)处不断向 +y 方向发射出大量质量为 m、带电量为 –q 的粒子,粒子的初速度大小广泛分布于零到 v0之间.已知这些粒子此后所经磁场的磁感应强度大小为 B,方向垂直于纸面向里,所有粒子都沿 +x 方向经过 b 区域,都沿 -y的方向通过点 N(3,0). (1)通过计算,求出符合要求的磁场范围的最小面积; (2)若其中速度为 k1v0 和 k2v0 的两个粒子同时到达 N 点(1>k1>k2>0),求二者发射的时间差.
例、质量均为m的一簇粒子在P点以同一速度v向不同方向散开(如图),垂直纸面的匀强磁场B将这些粒子聚焦于R点,距离PR=2a,离子的轨迹应是轴对称的.试确定磁场区域的边界.
解答:在磁场B中,粒子受洛仑兹力作用作半径为r的圆周运动:
设半径为r的圆轨道上运动的粒子,在点A (x,y)离开磁场,沿切线飞向R点.由相似三角形得到:
同时,A作为轨迹圆上的点,应满足方程:
x2+(y-b)=r2
消去(y-b),得到满足条件的A点的集合,因此,表示磁场边界的函数方程为:
2022-2023年高考物理一轮复习 磁场及带电粒子在磁场中的运动课件: 这是一份2022-2023年高考物理一轮复习 磁场及带电粒子在磁场中的运动课件,共56页。
高考物理一轮复习第9章磁场第4课时磁场中的动态圆磁聚焦磁发散问题课件: 这是一份高考物理一轮复习第9章磁场第4课时磁场中的动态圆磁聚焦磁发散问题课件,共36页。
2022-2023年高考物理一轮复习 带电粒子在有界磁场中的运动课件: 这是一份2022-2023年高考物理一轮复习 带电粒子在有界磁场中的运动课件,共19页。












