安徽省合肥市包河区四十八中学2022年中考联考数学试题含解析

2021-2022中考数学模拟试卷

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）

1．某工厂现在平均每天比原计划多生产50台机器，现在生产600台所需时间与原计划生产450台机器所需时间相同．设原计划平均每天生产x台机器，根据题意，下面所列方程正确的是（　　）

A．＝ B．＝

C．＝ D．＝

2．如图，已知Rt△ABC中，∠BAC=90°，将△ABC绕点A顺时针旋转，使点D落在射线CA上，DE的延长线交BC于F，则∠CFD的度数为（　　）

A．80° B．90° C．100° D．120°

3．6的相反数为　　

A．-6 B．6 C． D．

4．不等式的最小整数解是（   ）

A．－3 B．－2 C．－1 D．2

5．如图，Rt△ABC中，∠C=90°，∠A=35°，点D在边BC上，BD=2CD．把△ABC绕着点D逆时针旋转m（0＜m＜180）度后，如果点B恰好落在初始Rt△ABC的边上，那么m=（　　）

A．35° B．60° C．70° D．70°或120°

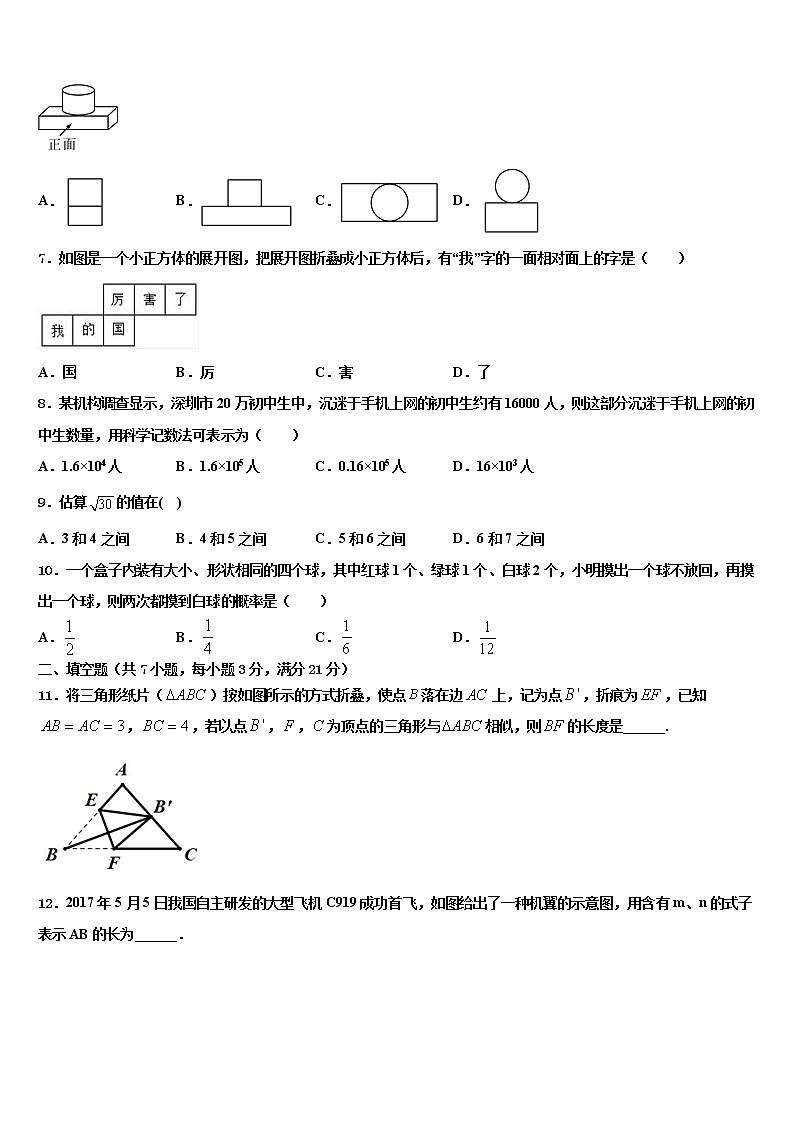
6．如图，是由一个圆柱体和一个长方体组成的几何体，其主视图是(    )

A． B． C． D．

7．如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“我”字的一面相对面上的字是（　　）

A．国 B．厉 C．害 D．了

8．某机构调查显示，深圳市20万初中生中，沉迷于手机上网的初中生约有16000人，则这部分沉迷于手机上网的初中生数量，用科学记数法可表示为（　　）

A．1.6×104人 B．1.6×105人 C．0.16×105人 D．16×103人

9．估算的值在(    )

A．3和4之间 B．4和5之间 C．5和6之间 D．6和7之间

10．一个盒子内装有大小、形状相同的四个球，其中红球1个、绿球1个、白球2个，小明摸出一个球不放回，再摸出一个球，则两次都摸到白球的概率是（　　）

A． B． C． D．

二、填空题（共7小题，每小题3分，满分21分）

11．将三角形纸片（）按如图所示的方式折叠，使点落在边上，记为点，折痕为，已知，，若以点，，为顶点的三角形与相似，则的长度是______.

12．2017年5月5日我国自主研发的大型飞机C919成功首飞，如图给出了一种机翼的示意图，用含有m、n的式子表示AB的长为______．

13．若使代数式有意义，则x的取值范围是_____．

14．如图，用10 m长的铁丝网围成一个一面靠墙的矩形养殖场，其养殖场的最大面积________m1．

15．某航空公司规定，旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定，则旅客可携带的免费行李的最大质量为            kg

16．已知一纸箱中，装有5个只有颜色不同的球，其中2个白球，3个红球，若往原纸箱中再放入x个白球，然后从箱中随机取出一个白球的概率是，则x的值为_____

17．如图，在□ABCD中，用直尺和圆规作∠BAD的平分线AG，若AD＝5，DE＝6，则AG的长是________．

三、解答题（共7小题，满分69分）

18．（10分）如图，一棵大树在一次强台风中折断倒下，未折断树杆与地面仍保持垂直的关系，而折断部分与未折断树杆形成的夹角．树杆旁有一座与地面垂直的铁塔，测得米，塔高米．在某一时刻的太阳照射下，未折断树杆落在地面的影子长为米，且点、、、在同一条直线上，点、、也在同一条直线上．求这棵大树没有折断前的高度．（结果精确到，参考数据：，，）．

19．（5分）中华文明，源远流长；中华汉字，寓意深广，为了传承优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了其中200名学生的成绩(成绩x取整数，总分100分)作为样本进行整理，得到下列不完整的统计图表：

请根据所给信息，解答下列问题：m＝　   　，n＝　   　；请补全频数分布直方图；若成绩在90分以上(包括90分)的为“优”等，则该校参加这次比赛的3000名学生中成绩“优”等约有多少人？

20．（8分）如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A、C分别在坐标轴上，点B的坐标为（4，2），直线交AB，BC分别于点M，N，反比例函数的图象经过点M，N．

求反比例函数的解析式；若点P在y轴上，且△OPM的面积与四边形BMON的面积相等，求点P的坐标．

21．（10分）小王是“新星厂”的一名工人，请你阅读下列信息：

信息一：工人工作时间：每天上午8：00﹣12：00，下午14：00﹣18：00，每月工作25天；

信息二：小王生产甲、乙两种产品的件数与所用时间的关系见下表：

信息三：按件计酬，每生产一件甲种产品得1.50元，每生产一件乙种产品得2.80元．

信息四：该厂工人每月收入由底薪和计酬工资两部分构成，小王每月的底薪为1900元，请根据以上信息，解答下列问题：

（1）小王每生产一件甲种产品，每生产一件乙种产品分别需要多少分钟；

（2）2018年1月工厂要求小王生产甲种产品的件数不少于60件，则小王该月收入最多是多少元？此时小王生产的甲、乙两种产品分别是多少件？

22．（10分）如图，B、E、C、F在同一直线上，AB＝DE，BE＝CF，∠B＝∠DEF，求证：AC＝DF．

23．（12分）先化简，再求值：，其中的值从不等式组的整数解中选取.

24．（14分）如图,矩形摆放在平面直角坐标系中,点在轴上,点在轴上,.

(1)求直线的表达式;

(2)若直线与矩形有公共点，求的取值范围;

(3)直线与矩形没有公共点，直接写出的取值范围.

参考答案

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）

1、B

【解析】
设原计划平均每天生产x台机器，则实际平均每天生产（x+50）台机器，根据题意可得：现在生产600台所需时间与原计划生产450台机器所需时间相同，据此列方程即可．

【详解】

设原计划平均每天生产x台机器，则实际平均每天生产（x+50）台机器，由题意得：．

故选B．

【点睛】

本题考查了由实际问题抽象出分式方程，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程．

2、B

【解析】
根据旋转的性质得出全等，推出∠B=∠D，求出∠B+∠BEF=∠D+∠AED=90°，根据三角形外角性质得出∠CFD=∠B+∠BEF，代入求出即可．

【详解】

解：∵将△ABC绕点A顺时针旋转得到△ADE，

∴△ABC≌△ADE，

∴∠B=∠D，

∵∠CAB=∠BAD=90°，∠BEF=∠AED，∠B+∠BEF+∠BFE=180°，∠D+∠BAD+∠AED=180°，

∴∠B+∠BEF=∠D+∠AED=180°﹣90°=90°，

∴∠CFD=∠B+∠BEF=90°，

故选：B．

【点睛】

本题考查了旋转的性质，全等三角形的性质和判定，三角形内角和定理，三角形外角性质的应用，掌握旋转变换的性质是解题的关键．

3、A

【解析】
根据相反数的定义进行求解.

【详解】

1的相反数为：﹣1．故选A.

【点睛】

本题主要考查相反数的定义，熟练掌握相反数的定义是解答的关键，绝对值相等，符号相反的两个数互为相反数.

4、B

【解析】
先求出不等式的解集，然后从解集中找出最小整数即可.

【详解】

∵，

∴，

∴，

∴不等式的最小整数解是x=-2.

故选B.

【点睛】

本题考查了一元一次不等式的解法，熟练掌握解一元一次不等式的步骤是解答本题的关键.最后一步系数化为1时，如果未知数的系数是负数，则不等号的方向要改变，如果系数是正数，则不等号的方不变.

5、D

【解析】
①当点B落在AB边上时，根据DB=DB1，即可解决问题，②当点B落在AC上时，在RT△DCB2中，根据∠C=90°，DB2=DB=2CD可以判定∠CB2D=30°，由此即可解决问题．

【详解】

①当点B落在AB边上时，

∵，

∴，

∴，

②当点B落在AC上时，

在中,

∵∠C=90°, ，

∴，

∴，

故选D.

【点睛】

本题考查的知识点是旋转的性质，解题关键是考虑多种情况，进行分类讨论.

6、B

【解析】

试题分析：长方体的主视图为矩形，圆柱的主视图为矩形，根据立体图形可得：主视图的上面和下面各为一个矩形，且下面矩形的长比上面矩形的长要长一点，两个矩形的宽一样大小．

考点：三视图．

7、A

【解析】
正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．

【详解】

∴有“我”字一面的相对面上的字是国.

故答案选A.

【点睛】

本题考查的知识点是专题：正方体相对两个面上的文字，解题的关键是熟练的掌握正方体相对两个面上的文字.

8、A

【解析】
科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞10时，n是正数；当原数的绝对值＜1时，n是负数．

【详解】

用科学记数法表示16000，应记作1.6×104，

故选A．

【点睛】

此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．

9、C

【解析】
由可知56，即可解出.

【详解】

∵

∴56，

故选C.

【点睛】

此题主要考查了无理数的估算，掌握无理数的估算是解题的关键.

10、C

【解析】
画树状图求出共有12种等可能结果，符合题意得有2种，从而求解.

【详解】

解：画树状图得：

∵共有12种等可能的结果，两次都摸到白球的有2种情况，

∴两次都摸到白球的概率是：．

故答案为C．

【点睛】

本题考查画树状图求概率，掌握树状图的画法准确求出所有的等可能结果及符合题意的结果是本题的解题关键．

二、填空题（共7小题，每小题3分，满分21分）

11、或2

【解析】
由折叠性质可知B’F=BF，△B’FC与△ABC相似，有两种情况，分别对两种情况进行讨论，设出B’F=BF=x，列出比例式方程解方程即可得到结果.

【详解】

由折叠性质可知B’F=BF，设B’F=BF=x，故CF=4-x

当△B’FC∽△ABC，有，得到方程，解得x=，故BF=；

当△FB’C∽△ABC，有，得到方程，解得x=2，故BF=2；

综上BF的长度可以为或2.

【点睛】

本题主要考查相似三角形性质，解题关键在于能够对两个相似三角形进行分类讨论.

12、

【解析】
过点C作CE⊥CF延长BA交CE于点E,先求得DF的长,可得到AE的长,最后可求得AB的长.

【详解】

解：延长BA交CE于点E，设CF⊥BF于点F，如图所示．

在Rt△BDF中，BF＝n，∠DBF＝30°，

∴．

在Rt△ACE中，∠AEC＝90°，∠ACE＝45°，

∴AE＝CE＝BF＝n，

∴．

故答案为：．

【点睛】

此题考查解直角三角形的应用,解题的关键在于做辅助线.

13、x≠﹣2

【解析】
直接利用分式有意义则其分母不为零，进而得出答案．

【详解】

∵分式有意义，

∴x的取值范围是：x+2≠0，

解得：x≠−2.

故答案是：x≠−2.

【点睛】

本题考查了分式有意义的条件，解题的关键是熟练的掌握分式有意义的条件.

14、2

【解析】

设与墙平行的一边长为xm，则另一面为 ，

其面积=，

∴最大面积为 ；

即最大面积是2m1．

故答案是2．

【点睛】求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法，常用的是后两种方法，当二次系数a的绝对值是较小的整数时，用配方法较好，如y=-x1-1x+5，y=3x1-6x+1等用配方法求解比较简单．

15、20

【解析】

设函数表达式为y=kx+b把（30，300）、（50、900）代入可得：y=30x-600当y=0时x=20所以免费行李的最大质量为20kg

16、1．

【解析】
先根据概率公式得到，解得.

【详解】

根据题意得，

解得.

故答案为：.

【点睛】

本题考查了概率公式：随机事件的概率事件可能出现的结果数除以所有可能出现的结果数.

17、2

【解析】

试题解析：连接EG，

∵由作图可知AD=AE，AG是∠BAD的平分线，
∴∠1=∠2，
∴AG⊥DE，OD=DE=1．
∵四边形ABCD是平行四边形，
∴CD∥AB，
∴∠2=∠1，
∴∠1=∠1，
∴AD=DG．
∵AG⊥DE，
∴OA=AG．
在Rt△AOD中，OA==4，
∴AG=2AO=2．
故答案为2.

三、解答题（共7小题，满分69分）

18、米．

【解析】

试题分析：要求这棵大树没有折断前的高度，只要求出AB和AC的长度即可，根据题目中的条件可以求得AB和AC的长度，即可得到结论．

试题解析：解：∵AB⊥EF，DE⊥EF，∴∠ABC=90°，AB∥DE，∴△FAB∽△FDE，∴ ，∵FB=4米，BE=6米，DE=9米，∴，得AB=3.6米，∵∠ABC=90°，∠BAC=53°，cos∠BAC=，∴AC= ==6米，∴AB+AC=3.6+6=9.6米，即这棵大树没有折断前的高度是9.6米．

点睛：本题考查直角三角形的应用，解题的关键是明确题意，找出所求问题需要的条件，利用锐角三角函数进行解答．

19、（1）70，0.2（2）70（3）750

【解析】
（1）根据题意和统计表中的数据可以求得m、n的值；

（2）根据（1）中求得的m的值，从而可以将条形统计图补充完整；

（3）根据统计表中的数据可以估计该校参加这次比赛的3000名学生中成绩“优”等约有多少人．

【详解】

解：（1）由题意可得，

m＝200×0.35＝70，n＝40÷200＝0.2，

故答案为70，0.2；

（2）由（1）知，m＝70，

补全的频数分布直方图，如下图所示；

（3）由题意可得，

该校参加这次比赛的3000名学生中成绩“优”等约有：3000×0.25＝750（人），

答：该校参加这次比赛的3000名学生中成绩“优”等约有750人．

【点睛】

本题考查频数分布直方图、频数分布表、用样本估计总体，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．

20、（1）；（2）点P的坐标是（0，4）或（0，－4）.

【解析】
（1）求出OA=BC=2，将y=2代入求出x=2，得出M的坐标，把M的坐标代入反比例函数的解析式即可求出答案.

（2）求出四边形BMON的面积，求出OP的值，即可求出P的坐标.

【详解】

（1）∵B（4，2），四边形OABC是矩形，

∴OA=BC=2.

将y=2代入3得：x=2，∴M（2，2）.

把M的坐标代入得：k=4，

∴反比例函数的解析式是；

（2）.

∵△OPM的面积与四边形BMON的面积相等，

∴.

∵AM=2，

∴OP=4.

∴点P的坐标是（0，4）或（0，－4）.

21、（1）生产一件甲产品需要15分，生产一件乙产品需要20分；（2）小王该月最多能得3544元，此时生产甲、乙两种产品分别60，555件．

【解析】
（1）设生产一件甲种产品需x分，生产一件乙种产品需y分，利用待定系数法求出x，y的值．
（2）设生产甲种产品用x分，则生产乙种产品用（25×8×60-x）分，分别求出甲乙两种生产多少件产品．

【详解】

（1）设生产一件甲种产品需x分，生产一件乙种产品需y分．

由题意得：，

解这个方程组得：，

答：生产一件甲产品需要15分，生产一件乙产品需要20分．

（2）设生产甲种产品共用x分，则生产乙种产品用（25×8×60-x）分．

则生产甲种产品件，生产乙种产品件．

∴w总额=1.5×+2.8×=0.1x+×2.8=0.1x+1680-0.14x=-0.04x+1680，

又≥60，得x≥900，

由一次函数的增减性，当x=900时w取得最大值，此时w=0.04×900+1680=1644（元），

则小王该月收入最多是1644+1900=3544（元），

此时甲有=60（件），

乙有：=555（件），

答：小王该月最多能得3544元，此时生产甲、乙两种产品分别60，555件．

【点睛】

考查了一次函数和二元一次方程组的应用．解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程组，再求解．

22、见解析

【解析】
由BE＝CF可得BC＝EF，即可判定，再利用全等三角形的性质证明即可．

【详解】

∵BE＝CF，

∴，

即BC＝EF，

又∵AB＝DE，∠B＝∠DEF，

∴在与中，

，

∴，

∴AC＝DF．

【点睛】

本题主要考查了三角形全等的判定，熟练掌握三角形全等的判定定理是解决本题的关键.

23、-2.

【解析】

试题分析：先算括号里面的，再算除法，解不等式组，求出x的取值范围，选出合适的x的值代入求值即可．

试题解析：原式=

==

解得-1≤x<，

∴不等式组的整数解为-1，0，1，2

 若分式有意义，只能取x=2，

∴原式=-=－2

【点睛】本题考查的是分式的化简求值，分式中的一些特殊求值题并非是一味的化简，代入，求值．许多问题还需运用到常见的数学思想，如化归思想（即转化）、整体思想等，了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助．

24、（1）；（2）；（3）

【解析】
（1）由条件可求得A、C的坐标，利用待定系数法可求得直线AC的表达式；

（2）结合图形，当直线平移到过C、A时与矩形有一个公共点，则可求得b的取值范围；

（3）由题意可知直线l过（0，10），结合图象可知当直线过B点时与矩形有一个公共点，结合图象可求得k的取值范围．

【详解】

解:

(1)

，

设直线表达式为,

，解得

直线表达式为;

(2) 直线可以看到是由直线平移得到,

当直线过时，直线与矩形有一个公共点,如图1，

当过点时,代入可得,解得.

当过点时,可得

直线与矩形有公共点时，的取值范围为;

(3) ,

直线过，且,

如图2，直线绕点旋转,当直线过点时,与矩形有一个公共点,逆时针旋转到与轴重合时与矩形有公共点,

当过点时,代入可得,解得

直线:与矩形没有公共点时的取值范围为

【点睛】

本题为一次函数的综合应用，涉及待定系数法、直线的平移、旋转及数形结合思想等知识．在（1）中利用待定系数法是解题的关键，在（2）、（3）中确定出直线与矩形OABC有一个公共点的位置是解题的关键．本题考查知识点较多，综合性较强，难度适中．