2022年云南省昆明市仁德一中重点中学中考联考数学试题含解析

这是一份2022年云南省昆明市仁德一中重点中学中考联考数学试题含解析，共19页。试卷主要包含了某商品的进价为每件元等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。

一、选择题（共10小题，每小题3分，共30分）
1．如图，△ABC中，AB>AC，∠CAD为△ABC的外角，观察图中尺规作图的痕迹，则下列结论错误的是（ ）

A．∠DAE=∠B B．∠EAC=∠C C．AE∥BC D．∠DAE=∠EAC
2．每到四月，许多地方杨絮、柳絮如雪花般漫天飞舞，人们不堪其忧，据测定，杨絮纤维的直径约为0.0000105m，该数值用科学记数法表示为（ ）
A．1.05×105 B．0.105×10﹣4 C．1.05×10﹣5 D．105×10﹣7
3．如图，直线m⊥n，在某平面直角坐标系中，x轴∥m，y轴∥n，点A的坐标为（－4，2），点B的坐标为（2，－4），则坐标原点为（ ）

A．O1 B．O2 C．O3 D．O4
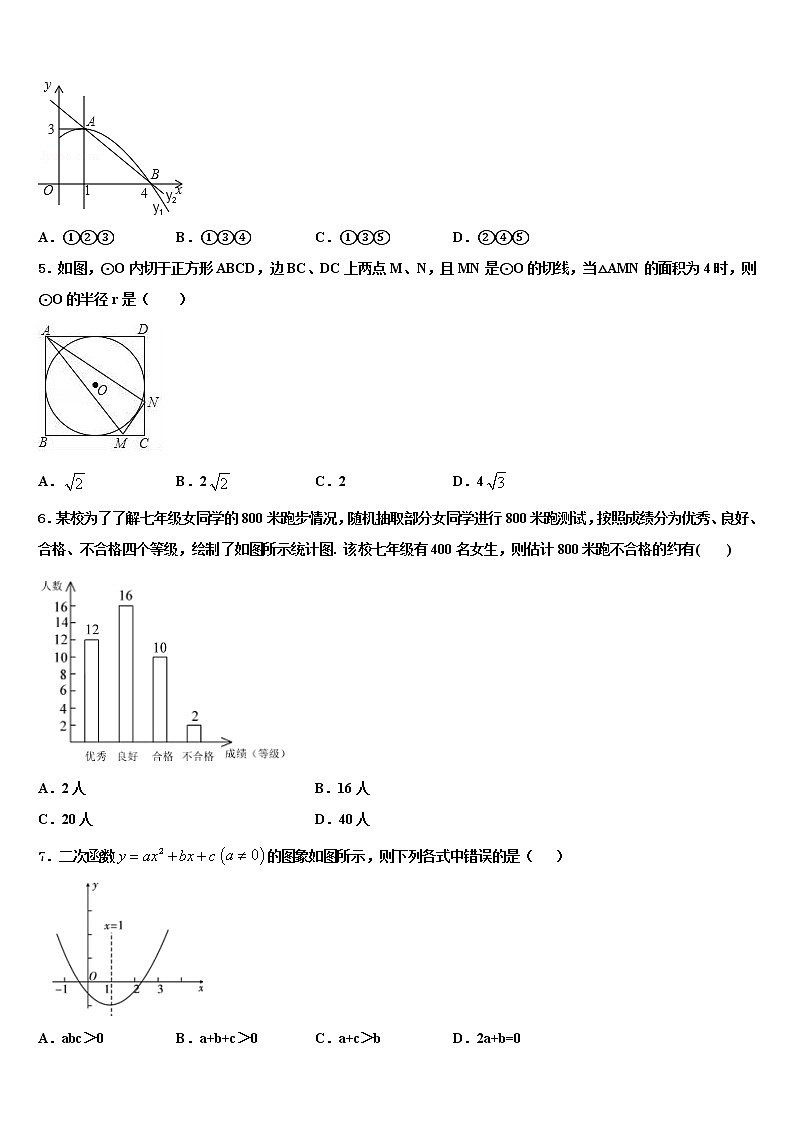
4．如图是抛物线y1=ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点B（4，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论：
①2a+b=0；②abc＞0；③方程ax2+bx+c=3有两个相等的实数根；④抛物线与x轴的另一个交点是（﹣1，0）；⑤当1＜x＜4时，有y2＜y1，
其中正确的是（ ）

A．①②③ B．①③④ C．①③⑤ D．②④⑤
5．如图，⊙O内切于正方形ABCD，边BC、DC上两点M、N，且MN是⊙O的切线，当△AMN的面积为4时，则⊙O的半径r是（　　）

A． B．2 C．2 D．4
6．某校为了了解七年级女同学的800米跑步情况，随机抽取部分女同学进行800米跑测试，按照成绩分为优秀、良好、合格、不合格四个等级，绘制了如图所示统计图. 该校七年级有400名女生，则估计800米跑不合格的约有( )

A．2人 B．16人
C．20人 D．40人
7．二次函数的图象如图所示，则下列各式中错误的是（ ）

A．abc＞0 B．a+b+c＞0 C．a+c＞b D．2a+b=0
8．某商品的进价为每件元．当售价为每件元时，每星期可卖出件，现需降价处理，为占有市场份额，且经市场调查：每降价元，每星期可多卖出件．现在要使利润为元，每件商品应降价（ ）元．
A．3 B．2.5 C．2 D．5
9．已知一元二次方程x2-8x+15=0的两个解恰好分别是等腰△ABC的底边长和腰长，则△ABC的周长为（ ）
A．13 B．11或13 C．11 D．12
10．a≠0，函数y＝与y＝﹣ax2+a在同一直角坐标系中的大致图象可能是（　　）
A． B．
C． D．
二、填空题（本大题共6个小题，每小题3分，共18分）
11．的相反数是______．
12．关于的一元二次方程有两个不相等的实数根，则实数的取值范围是________．
13．如图，直线m∥n，△ABC为等腰直角三角形，∠BAC=90°，则∠1= 度．

14．一个多边形的内角和比它的外角和的3倍少180°，则这个多边形的边数是______.
15．小华到商场购买贺卡，他身上带的钱恰好能买5张3D立体贺卡或20张普通贺卡若小华先买了3张3D立体贺卡，则剩下的钱恰好还能买______张普通贺卡．
16．若+(y﹣2018)2＝0，则x﹣2+y0＝_____．
三、解答题（共8题，共72分）
17．（8分）如图，点O是△ABC的边AB上一点，⊙O与边AC相切于点E，与边BC，AB分别相交于点D，F，且DE=EF．求证：∠C=90°；当BC=3，sinA=时，求AF的长．

18．（8分）如图，已知AD是的中线，M是AD的中点，过A点作，CM的延长线与AE相交于点E，与AB相交于点F.

（1）求证：四边形是平行四边形；
（2）如果，求证四边形是矩形.
19．（8分）某通讯公司推出了A，B两种上宽带网的收费方式（详情见下表）

设月上网时间为x h（x为非负整数），请根据表中提供的信息回答下列问题
（1）设方案A的收费金额为y1元，方案B的收费金额为y2元，分别写出y1，y2关于x的函数关系式；
（2）当35＜x＜50时，选取哪种方式能节省上网费，请说明理由
20．（8分）如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交BC，AC于点D，E，DG⊥AC于点G，交AB的延长线于点F．

（1）求证：直线FG是⊙O的切线；
（2）若AC=10，cosA=，求CG的长．
21．（8分）有两把不同的锁和四把不同的钥匙，其中两把钥匙恰好分别能打开这两把锁，其余的钥匙不能打开这两把锁．现在任意取出一把钥匙去开任意一把锁．
（1）请用列表或画树状图的方法表示出上述试验所有可能结果；
（2）求一次打开锁的概率．
22．（10分）如图，在平行四边形ABCD中，E为BC边上一点，连结AE、BD且AE=AB．
求证：∠ABE=∠EAD；若∠AEB=2∠ADB，求证：四边形ABCD是菱形．
23．（12分）太原市志愿者服务平台旨在弘扬“奉献、关爱、互助、进步”的志愿服务精神，培育志思服务文化，推动太原市志愿服务的制度化、常态化，弘扬社会正能量，截止到2018年5月9日16：00，在该平台注册的志愿组织数达2678个，志愿者人数达247951人，组织志愿活动19748次，累计志愿服务时间3889241小时，学校为了解共青团员志愿服务情况，调查小组根据平台数据进行了抽样问卷调查，过程如下：
（1）收集、整理数据：
从九年级随机抽取40名共青团员，将其志愿服务时间按如下方式分组（A：0～5小时；B：5～10小时；C：10～15小时；D：15～20小时；E：20～25小时；F：25～30小时，注：每组含最小值，不含最大值）得到这40名志愿者服务时间如下：
B D E A C E D B F C D D D B E C D E E F
A F F A D C D B D F C F D E C E E E C E
并将上述数据整理在如下的频数分布表中，请你补充其中的数据：
志愿服务时间
A
B
C
D
E
F
频数
3
4
　 　
10
　 　
7
（2）描述数据：
根据上面的频数分布表，小明绘制了如下的频数直方图（图1），请将空缺的部分补充完整；
（3）分析数据：
①调查小组从八年级共青团员中随机抽取40名，将他们的志愿服务时间按（1）题的方式整理后，画出如图2的扇形统计图．请你对比八九年级的统计图，写出一个结论；
②校团委计划组织志愿服务时间不足10小时的团员参加义务劳动，根据上述信息估计九年级200名团员中参加此次义务劳动的人数约为　 　人；
（4）问题解决：
校团委计划组织中考志愿服务活动，共甲、乙、丙三个服务点，八年级的小颖和小文任意选择一个服务点参与志服务，求两人恰好选在同一个服务点的概率．

24．“母亲节”前夕，某商店根据市场调查，用3000元购进第一批盒装花，上市后很快售完，接着又用5000元购进第二批这种盒装花．已知第二批所购花的盒数是第一批所购花盒数的2倍，且每盒花的进价比第一批的进价少5元．求第一批盒装花每盒的进价是多少元？



参考答案

一、选择题（共10小题，每小题3分，共30分）
1、D
【解析】
解：根据图中尺规作图的痕迹，可得∠DAE=∠B，故A选项正确，
∴AE∥BC，故C选项正确，
∴∠EAC=∠C，故B选项正确，
∵AB＞AC，∴∠C＞∠B，∴∠CAE＞∠DAE，故D选项错误，
故选D．
【点睛】
本题考查作图—复杂作图；平行线的判定与性质；三角形的外角性质．
2、C
【解析】
试题分析：绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．所以0.0000105=1.05×10﹣5，故选C．
考点：科学记数法．
3、A
【解析】
试题分析：因为A点坐标为（－4，2），所以，原点在点A的右边，也在点A的下边2个单位处，从点B来看，B（2，－4），所以，原点在点B的左边，且在点B的上边4个单位处．如下图，O1符合．

考点：平面直角坐标系．
4、C
【解析】
试题解析：∵抛物线的顶点坐标A（1，3），
∴抛物线的对称轴为直线x=-=1，
∴2a+b=0，所以①正确；
∵抛物线开口向下，
∴a＜0，
∴b=-2a＞0，
∵抛物线与y轴的交点在x轴上方，
∴c＞0，
∴abc＜0，所以②错误；
∵抛物线的顶点坐标A（1，3），
∴x=1时，二次函数有最大值，
∴方程ax2+bx+c=3有两个相等的实数根，所以③正确；
∵抛物线与x轴的一个交点为（4，0）
而抛物线的对称轴为直线x=1，
∴抛物线与x轴的另一个交点为（-2，0），所以④错误；
∵抛物线y1=ax2+bx+c与直线y2=mx+n（m≠0）交于A（1，3），B点（4，0）
∴当1＜x＜4时，y2＜y1，所以⑤正确．
故选C．
考点：1.二次函数图象与系数的关系；2.抛物线与x轴的交点．
5、C
【解析】
连接,交于点设则根据△AMN的面积为4，列出方程求出的值，再计算半径即可.
【详解】
连接,交于点

内切于正方形 为的切线，
经过点 为等腰直角三角形，

为的切线，

设则
△AMN的面积为4，
则
即解得

故选:C.
【点睛】
考查圆的切线的性质，等腰直角三角形的性质，三角形的面积公式，综合性比较强.
6、C
【解析】
先求出800米跑不合格的百分率，再根据用样本估计总体求出估值．
【详解】
400×人.
故选C．
【点睛】
考查了频率分布直方图，以及用样本估计总体，关键是从上面可得到具体的值．
7、B
【解析】
根据二次函数的图象与性质逐一判断即可．
【详解】
解：由图象可知抛物线开口向上，
∴，
∵对称轴为，
∴，
∴，
∴，故D正确，
又∵抛物线与y轴交于y轴的负半轴，
∴，
∴，故A正确；
当x=1时，，
即，故B错误；
当x=-1时，
即，
∴，故C正确，
故答案为：B．
【点睛】
本题考查了二次函数图象与系数之间的关系，解题的关键是熟练掌握二次函数各系数的意义以及二次函数的图象与性质．
8、A
【解析】
设售价为x元时，每星期盈利为6125元，那么每件利润为（x-40），原来售价为每件60元时，每星期可卖出300件，所以现在可以卖出[300+20（60-x）]件，然后根据盈利为6120元即可列出方程解决问题．
【详解】
解：设售价为x元时，每星期盈利为6120元，
由题意得（x-40）[300+20（60-x）]=6120，
解得：x1=57，x2=1，
由已知，要多占市场份额，故销售量要尽量大，即售价要低，故舍去x2=1．
∴每件商品应降价60-57=3元．
故选：A．
【点睛】
本题考查了一元二次方程的应用．此题找到关键描述语，找到等量关系准确的列出方程是解决问题的关键．此题要注意判断所求的解是否符合题意，舍去不合题意的解．
9、B
【解析】
试题解析：x2-8x+15=0，
分解因式得：（x-3）（x-5）=0，
可得x-3=0或x-5=0，
解得：x1=3，x2=5，
若3为底边，5为腰时，三边长分别为3，5，5，周长为3+5+5=1；
若3为腰，5为底边时，三边长分别为3，3，5，周长为3+3+5=11，
综上，△ABC的周长为11或1．
故选B.
考点：1.解一元二次方程-因式分解法；2.三角形三边关系；3.等腰三角形的性质．
10、D
【解析】
分a＞0和a＜0两种情况分类讨论即可确定正确的选项
【详解】
当a＞0时，函数y＝ 的图象位于一、三象限，y＝﹣ax2+a的开口向下，交y轴的正半轴，没有符合的选项，
当a＜0时，函数y＝的图象位于二、四象限，y＝﹣ax2+a的开口向上，交y轴的负半轴，D选项符合；
故选D．
【点睛】
本题考查了反比例函数的图象及二次函数的图象的知识，解题的关键是根据比例系数的符号确定其图象的位置，难度不大．

二、填空题（本大题共6个小题，每小题3分，共18分）
11、﹣．
【解析】
根据只有符号不同的两个数叫做互为相反数解答．
【详解】
的相反数是.
故答案为.
【点睛】
本题考查的知识点是相反数，解题关键是熟记相反数的概念.
12、b＜9
【解析】
由方程有两个不相等的实数根结合根的判别式，可得出，解之即可得出实数b的取值范围．
【详解】
解：方程有两个不相等的实数根，
，
解得：．
【点睛】
本题考查的知识点是根的判别式，解题关键是牢记“当时，方程有两个不相等的实数根”．
13、1．
【解析】
试题分析：∵△ABC为等腰直角三角形，∠BAC=90°，∴∠ABC=∠ACB=1°，∵m∥n，∴∠1=1°；故答案为1．
考点：等腰直角三角形；平行线的性质．
14、7
【解析】
根据多边形内角和公式得：（n-2） .得：

15、1
【解析】
根据已知他身上带的钱恰好能买5张3D立体贺卡或20张普通贺卡得：1张3D立体贺卡的单价是1张普通贺卡单价的4倍，所以设1张3D立体贺卡x元，剩下的钱恰好还能买y张普通贺卡，根据3张3D立体贺卡张普通贺卡张3D立体贺卡，可得结论．
【详解】
解：设1张3D立体贺卡x元，剩下的钱恰好还能买y张普通贺卡．
则1张普通贺卡为：元，
由题意得：，
，
答：剩下的钱恰好还能买1张普通贺卡．
故答案为：1．
【点睛】
本题考查了一元一次方程的应用以及列代数式，解题的关键是：根据总价单价数量列式计算．
16、1
【解析】
直接利用偶次方的性质以及二次根式的性质分别化简得出答案．
【详解】
解：∵+(y﹣1018)1＝0，
∴x﹣1＝0，y﹣1018＝0，
解得：x＝1，y＝1018，
则x﹣1+y0＝1﹣1+10180＝1+1＝1．
故答案为：1．
【点睛】
此题主要考查了非负数的性质，正确得出x，y的值是解题关键．

三、解答题（共8题，共72分）
17、（1）见解析（2）
【解析】
（1）连接OE，BE，因为DE=EF，所以=，从而易证∠OEB=∠DBE，所以OE∥BC，从可证明BC⊥AC；
（2）设⊙O的半径为r，则AO=5﹣r，在Rt△AOE中，sinA=从而可求出r的值．
【详解】
解:（1）连接OE，BE，
∵DE=EF，
∴=
∴∠OBE=∠DBE
∵OE=OB，
∴∠OEB=∠OBE
∴∠OEB=∠DBE，
∴OE∥BC
∵⊙O与边AC相切于点E，
∴OE⊥AC
∴BC⊥AC
∴∠C=90°
（2）在△ABC，∠C=90°，BC=3，sinA=，
∴AB=5，
设⊙O的半径为r，则AO=5﹣r，
在Rt△AOE中，sinA=
∴
∴

【点睛】
本题考查圆的综合问题，涉及平行线的判定与性质，锐角三角函数，解方程等知识，综合程度较高，需要学生灵活运用所学知识．
18、（1）见解析；（2）见解析.
【解析】
（1）先判定，可得，再根据是的中线，即可得到，依据，即可得出四边形是平行四边形；
（2）先判定，即可得到，依据，可得根据是的中线，可得，进而得出四边形是矩形.
【详解】
证明：（1）是的中点，
，
，
，
又，
，
，
又是的中线，
，
又，
四边形是平行四边形；
（2），
，
∴，即，
，
又，
，
又是的中线，
，
又四边形是平行四边形，
四边形是矩形.

【点睛】
本题主要考查了平行四边形、矩形的判定，等腰三角形的性质以及相似三角形的性质的运用，解题时注意：对角线相等的平行四边形是矩形.
19、（1），；（2）当35＜x＜1时，选择B方式能节省上网费，见解析.
【解析】
（1）根据两种方式的收费标准，进行分类讨论即可求解；
（2）当35＜x＜1时，计算出y1-y2的值，即可得出答案．
【详解】
解：（1）由题意得：；
即；
；
即；
（2）选择B方式能节省上网费
当35＜x＜1时，有y1＝3x－45，y2＝1．
:y1-y2=3x－45－1＝3x－2．记y＝3x-2
因为3＞4，有y随x的增大而增大
当x＝35时，y＝3．
所以当35＜x＜1时，有y＞3，即y＞4．
所以当35＜x＜1时，选择B方式能节省上网费
【点睛】
此题考查了一次函数的应用，注意根据图表得出解题需要的信息，难度一般，正确理解收费标准求出函数解析式是解题的关键．
20、（3）证明见试题解析；（3）3．
【解析】
试题分析：（3）先得出OD∥AC，有∠ODG=∠DGC，再由DG⊥AC，得到∠DGC=90°，∠ODG=90°，得出OD⊥FG，即可得出直线FG是⊙O的切线．
（3）先得出△ODF∽△AGF，再由cosA=，得出cos∠DOF=；然后求出OF、AF的值，即可求出AG、CG的值．
试题解析：（3）如图3，连接OD，∵AB=AC，∴∠C=∠ABC，∵OD=OB，∴∠ABC=∠ODB，∴∠ODB=∠C，∴OD∥AC，∴∠ODG=∠DGC，∵DG⊥AC，∴∠DGC=90°，∴∠ODG=90°，∴OD⊥FG，∵OD是⊙O的半径，∴直线FG是⊙O的切线；
（3）如图3，∵AB=AC=30，AB是⊙O的直径，∴OA=OD=30÷3=5，由（3），可得：OD⊥FG，OD∥AC，∴∠ODF=90°，∠DOF=∠A，在△ODF和△AGF中，∵∠DOF=∠A，∠F=∠F，∴△ODF∽△AGF，∴，∵cosA=，∴cos∠DOF=，∴OF===，∴AF=AO+OF==，∴，解得AG=7，∴CG=AC﹣AG=30﹣7=3，即CG的长是3．

考点：3．切线的判定；3．相似三角形的判定与性质；3．综合题．
21、（1）详见解析（2）
【解析】
设两把不同的锁分别为A、B，能把两锁打开的钥匙分别为、，其余两把钥匙分别为、，根据题意，可以画出树形图，再根据概率公式求解即可.
【详解】
（1）设两把不同的锁分别为A、B，能把两锁打开的钥匙分别为、，其余两把钥匙分别为、，根据题意，可以画出如下树形图：

由上图可知，上述试验共有8种等可能结果；
（2）由（1）可知，任意取出一把钥匙去开任意一把锁共有8种可能的结果，一次打开锁的结果有2种，且所有结果的可能性相等．
∴P（一次打开锁）＝．
【点睛】
如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率．
22、（1）证明见解析；（2）证明见解析．
【解析】
（1）根据平行四边形的对边互相平行可得AD∥BC，再根据两直线平行，内错角相等可得∠AEB=∠EAD，根据等边对等角可得∠ABE=∠AEB，即可得证．
（2）根据两直线平行，内错角相等可得∠ADB=∠DBE，然后求出∠ABD=∠ADB，再根据等角对等边求出AB=AD，然后利用邻边相等的平行四边形是菱形证明即可．
【详解】
证明：（1）∵在平行四边形ABCD中，AD∥BC，
∴∠AEB=∠EAD．
∵AE=AB，
∴∠ABE=∠AEB．
∴∠ABE=∠EAD．
（2）∵AD∥BC，
∴∠ADB=∠DBE．
∵∠ABE=∠AEB，∠AEB=2∠ADB，
∴∠ABE=2∠ADB．
∴∠ABD=∠ABE－∠DBE=2∠ADB－∠ADB=∠ADB．
∴AB=AD．
又∵四边形ABCD是平行四边形，
∴四边形ABCD是菱形．
23、（1）7，9；（2）见解析;（3）①在15～20小时的人数最多；②35；（4）.
【解析】
（1）观察统计图即可得解；
（2）根据题意作图；
（3）①根据两个统计图解答即可；
②根据图1先算出不足10小时的概率再乘以200人即可；
（4）根据题意画出树状图即可解答.
【详解】
解：（1）C的频数为7，E的频数为9；
故答案为7，9；
（2）补全频数直方图为：

（3）①八九年级共青团员志愿服务时间在15～20小时的人数最多；
②200×=35，
所以估计九年级200名团员中参加此次义务劳动的人数约为35人；
故答案为35；
（4）画树状图为：

共有9种等可能的结果数，其中两人恰好选在同一个服务点的结果数为3，
所以两人恰好选在同一个服务点的概率==．
【点睛】
本题考查了条形统计图与扇形统计图与树状图法，解题的关键是熟练的掌握条形统计图与扇形统计图与树状图法.
24、30元
【解析】
试题分析：设第一批盒装花的进价是x元/盒，则第一批进的数量是：，第二批进的数量是：，再根据等量关系：第二批进的数量=第一批进的数量×2可得方程．
解：设第一批盒装花的进价是x元/盒，则
2×=，
解得 x=30
经检验，x=30是原方程的根．
答：第一批盒装花每盒的进价是30元．
考点：分式方程的应用．