2021-2022学年江西省赣州市南康区七年级（下）期末数学试卷（Word解析版）

绝密★启用前

2021-2022学年江西省赣州市南康区七年级（下）期末数学试卷

第I卷（选择题）

一、选择题（本大题共6小题，共18.0分。在每小题列出的选项中，选出符合题目的一项）

1. 在平面直角坐标系中，已知点，则点在(    )

A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

2. 下列说法中正确的是(    )

A. 的算术平方根是 B. 的平方根是
C. 的立方根是 D. 没有立方根

3. 已知：点，点关于轴对称，则的值(    )

A.  B.  C.  D.

4. 九章算术是中国传统数学的重要著作，方程术是它的最高成就．其中记载：今有共买物，人出八，盈三：人出七，不足四，问人数、物价各几何？译文：今有人合伙购物，每人出钱，会多钱；每人出钱，又会差钱，问人数、物价各是多少？设合伙人数为人，物价为钱，以下列出的方程组正确的是(    )

A.  B.  C.  D.

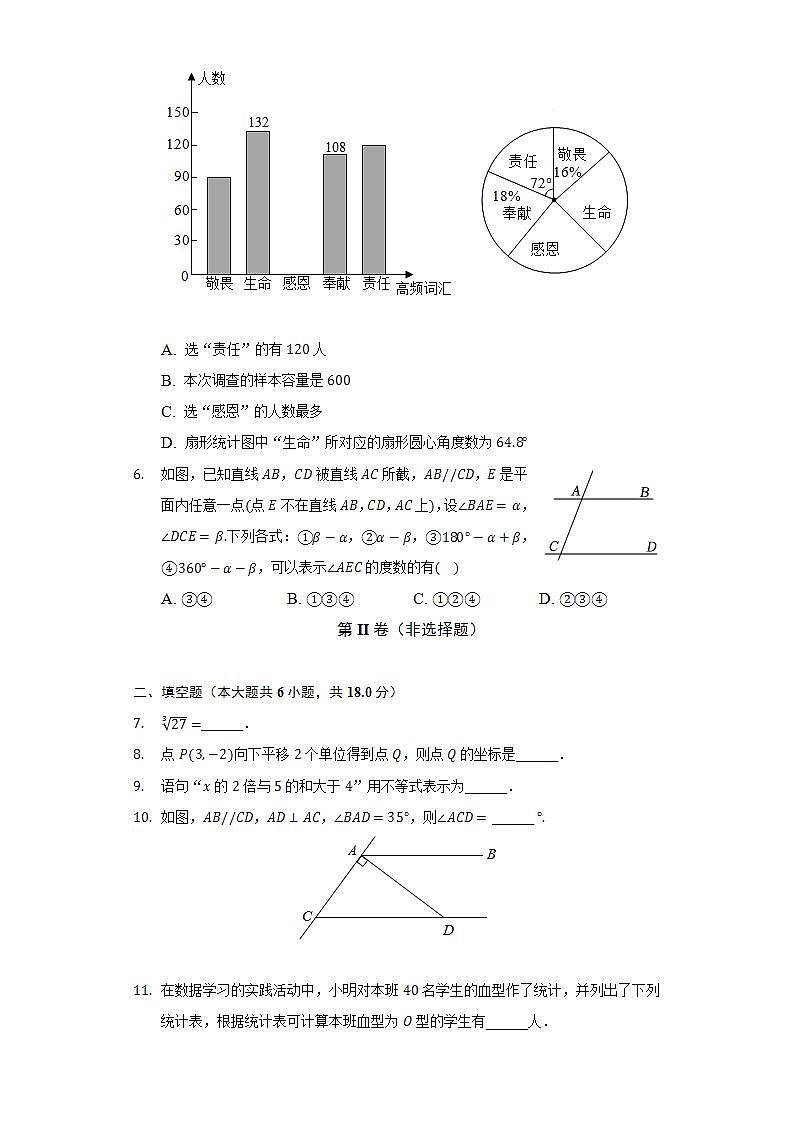
5. 为了调查疫情对青少年人生观、价值观产生的影响，某学校团委对初一级部学生进行了问卷调查，其中一项是：疫情期间出现的哪一个高频词汇最触动你的内心？针对该项调查结果制作的两个统计图不完整如图．由图中信息可知，下列结论错误的是(    )

A. 选“责任”的有人
B. 本次调查的样本容量是
C. 选“感恩”的人数最多
D. 扇形统计图中“生命”所对应的扇形圆心角度数为

6. 如图，已知直线，被直线所截，，是平面内任意一点点不在直线，，上，设，下列各式：，，，，可以表示的度数的有(    )

A.  B.  C.  D.

第II卷（非选择题）

二、填空题（本大题共6小题，共18.0分）

7. ______．
8. 点向下平移个单位得到点，则点的坐标是______．
9. 语句“的倍与的和大于”用不等式表示为______．
10. 如图，，，，则 ______

11. 在数据学习的实践活动中，小明对本班名学生的血型作了统计，并列出了下列统计表，根据统计表可计算本班血型为型的学生有______人．

12. 在平面直角坐标系中，有点，点，若在坐标轴上有一点不与点重合，使三角形和三角形面积相等，则点的坐标为______．

三、解答题（本大题共10小题，共64.0分。解答应写出文字说明，证明过程或演算步骤）

13. 计算：．
14. 解方程组：．
15. 填写以下推理过程中的理由：
    已知：如图，，，求证：．
    证明：已知，
    __________________
    已知，
    __________________
    ______

16. 取哪些整数值时，不等式和都成立？请通过计算进行说明．
17. 如图，在的方格纸中，每个小正方形的边长为一个长度单位，点、、都在格点上．
    将线段向上平移个单位得到线段，在方格纸中画出线段，连接，；
    三角形的面积______．

18. 为了解某校七年级学生身高情况，随机测量了位同学的身高单位：，并根据测得的数据绘制了两幅不完整的统计图，请结合图中提供的信息，解答下列问题：
    ______，所在扇形的圆心角度数是______；
    补全频数分布直方图；
    若该校七年级计划开展大课间体操比赛，要求每班应安排不低于本班人数的学生参加，并希望参赛学生的身高差距较小，请问你觉得应安排哪个范围的学生参赛更合适，并说说你的理由．
     

19. 已知关于，的二元一次方程组的解为．
    求，的值用含的代数式表示；
    若点在第四象限，求的取值范围．
20. 第题：计算下列各式的值：
    ；
    ．
    第题：有理数、、在数轴上的位置如图．
    用“”或“”填空： ______， ______， ______
    化简：．
     
21. 第题：有大小两种货车，辆大货车与辆小货车一次可以运货，辆大货车与辆小货车一次可以运货辆大货车与辆小货车一次可以运货多少？
    第题：为进一步提升摩托车、电动自行车骑乘人员和汽车驾乘人员安全防护水平，公安部交通管理局部署在全国开展“一盔一带”安全守护行动．某商店销售，两种头盔，进价和售价如表所示，请根据表格信息下列问题．
    该商店购进，两种头盔共个，用去元钱，求，两种头盔各购进了多少个？
    经过几天销售后商店发现销量较好，于是又用元钱购进这两种头盔若干个，要想将这两次购进的头盔售完后所获总利润不低于元，则该商店第二次至少应购进种头盔多少个？

22. 第题：如图，点，，分别是三角形的边，，上的点，已知，求证：．
    第题：已知，点在射线上，连接，，设，．
    如图，当点在线段上时，______用含，的式子表示；
    如图，当点在线段的延长线上时．
    判断与，的数量关系，并说明理由；
    若为平面内一动点，且，请直接写出与的数量关系．
     

答案和解析

1.【答案】 

【解析】解：点的横坐标大于，纵坐标小于，所以点所在的象限是第四象限．
故选：．
根据各象限内点的坐标特征解答即可．
本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限；第二象限；第三象限；第四象限．
 

2.【答案】 

【解析】解：的算术平方根是，因此选项A符合题意；
B.的平方根是，因此选项B不符合题意；
C.的立方根为，是的无理数，因此选项C不符合题意；
D.的立方根为，因此选项D不符合题意；
故选：．
根据平方根、算术平方根、立方根的定义逐项进行判断即可．
本题考查平方根、算术平方根、立方根，掌握平方根、算术平方根、立方根的定义是正确判断的前提．
 

3.【答案】 

【解析】解：点，点关于轴对称，
，，
故．
故选：．
根据关于轴的对称点的坐标特点：横坐标互为相反数，纵坐标不变可得答案．
此题主要考查了关于轴的对称点的坐标，关键是掌握点的坐标变化规律．
 

4.【答案】 

【解析】解：依题意，得：．
故选：．
根据“每人出钱，会多钱；每人出钱，又会差钱”，即可得出关于，的二元一次方程组，此题得解．
本题考查了由实际问题抽象出二元一次方程组，找准等量关系，正确列出二元一次方程组是解题的关键．
 

5.【答案】 

【解析】解：本次调查的样本容量为：，选“责任”的有人，故选项A中的说法正确，不符合题意；选项正确，不符合题意；
选“感恩”的人数为：，故选“感恩”的人数最多，故选项C中的说法正确，不符合题意；
扇形统计图中“生命”所对应的扇形圆心角度数为，故选项D中的说法错误，符合题意；
故选：．
根据条形统计图和扇形统计图中的数据，可以判断各个选项中的说法是否正确，从而可以解答本题．
本题考查条形统计图、扇形统计图，解答本题的关键是明确题意，利用数形结合的思想解答．
 

6.【答案】 

【解析】解：如图，由，可得，
，
．

如图，过作平行线，则由，可得，，
．

如图，由，可得，
，
．

如图，由，可得，
．

当点是和的交点时，，；
当点在的下方时，同理可得，或．
综上所述，的度数可能为，，，．
所以可以表示的度数的有，
故选：．
根据点有种可能位置，分情况进行讨论，依据平行线的性质以及三角形外角性质进行计算求解即可．
本题主要考查了平行线的性质的运用，解题时注意：两直线平行，同位角相等；两直线平行，内错角相等．
 

7.【答案】 

【解析】解：，
；
故答案为：．
，根据立方根的定义即可求出结果．
本题考查了立方根的定义；掌握开立方和立方互为逆运算是解题的关键．
 

8.【答案】 

【解析】解：点向下平移个单位得到点，
点的横坐标是，纵坐标为，即．
故答案为：．
将点的横坐标不变，纵坐标减去即可得到点的坐标．
本题考查图形的平移变换，关键是要懂得左右移动改变点的横坐标，左减、右加；上下移动改变点的纵坐标，下减、上加．
 

9.【答案】 

【解析】解：由题意得，．
故答案为：．
的两倍为，大于即“”，据此列不等式．
本题考查了有实际问题抽象出一元一次不等式，读懂题意，抓住关键词语，弄清运算的先后顺序和不等关系，才能把文字语言的不等关系转化为用数学符号表示的不等式．
 

10.【答案】 

【解析】解：，
，
，
，
，
故答案为：．
由平行线的性质得，再由垂线的定义可得三角形是直角三角形，进而得出的度数．
本题主要考查了平行线的性质，三角形内角和定理，垂线的定义，根据平行线的性质求出是解决问题的关键．
 

11.【答案】 

【解析】解：本班血型为型的学生有．
故选答案为：．
先求出型的频率，根据频数频率数据总数求解即可．
本题考查了频数分布表，，解答本题的关键是掌握频数频率数据总数．
 

12.【答案】，， 

【解析】解：根据题意可知三角形面积，
当点在轴上时，
，
，
解得，
点的坐标为，；
当点在轴上时，
，
，
，
又点不与点重合，
点坐标为．
综上所述，点的坐标为，，．
故答案为：，，．
根据题意点的位置可分当点在轴上时和当点在轴上时两种情况进行讨论，从而根据三角形的面积公式列出式子，，进而求得，得出点的坐标．
本题考查三角形的面积及坐标与图形性质，解题的关键是根据题意分两种情况进行讨论当点在轴上时和当点在轴上时，根据三角形的面积公式求得，再得出点的坐标，也可以适当的画草图进行分析．
 

13.【答案】解：原式
． 

【解析】直接利用二次根式的性质以及有理数的乘方运算法则、绝对值的性质分别化简，进而合并得出答案．
此题主要考查了实数的运算，正确化简各数是解题关键．
 

14.【答案】解：得：，
解得：，
把代入得：，
解得：，
则方程组解为． 

【解析】方程组利用加减消元法求出解即可．
此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
 

15.【答案】    内错角相等，两直线平行      同旁内角互补，两直线平行  平行于同一条直线的两条直线互相平行 

【解析】证明：已知，
内错角相等，两直线平行．
已知，
同旁内角互补，两直线平行．
平行于同一条直线的两条直线平行．
故答案为：，，内错角相等，两直线平行；，，同旁内角互补，两直线平行；平行于同一条直线的两条直线互相平行．
先根据平行线的判定，说明与、与间关系，再由平行线判定的推论得到结论．
本题考查了平行线的性质，题目难度不大，掌握平行线的判定方法是解决本题的关键．
 

16.【答案】解：由题意得：，
解不等式得：，
解不等式得：，
原不等式组的解集为：，
该不等式组的整数解为：，，，
当取，，时，不等式和都成立． 

【解析】根据题意可得，然后按照解一元一次不等式组的步骤，进行计算即可解答．
本题考查了解一元一次不等式组，熟练掌握解一元一次不等式组是解题的关键．
 

17.【答案】 

【解析】解：如图．

．
故答案为：．
根据平移的性质作图即可．
利用割补法求三角形的面积即可．
本题考查作图平移变换，熟练掌握平移的性质是解答本题的关键．
 

18.【答案】   

【解析】解：人，
所在扇形的圆心角度数为，
故答案为：，；
“”段的人数为人，
补全统计图如下：

由于“”组的占，符合“不低于”的学生参加，因此选择：比较合适．
从两个统计图可知，身高为“”段的有人，占调查人数的，根据频率可求出调查人数，即的值，求出“”段的占的百分比，即可求出相应的圆心角度数；
求出“”段的人数，即可补全条形统计图；
根据“每班不低于本班人数的学生参加”的要求，结合扇形统计图中各个身高段所占的百分比进行判断即可．
本题考查扇形统计图，频数分布直方图，掌握频率是正确解答的前提．
 

19.【答案】解：关于，的二元一次方程组的解为，
，
解得：；
点在第四象限，
，，
解得：，，
故的取值范围是：． 

【解析】把方程的解代入原方程，再利用加减消元法进行求解即可；
第四象限的点横坐标大于，纵坐标小于，据此可求解．
本题主要考查二元一次方程组的解，点的坐标，解答的关键是对相应的知识的掌握．
 

20.【答案】     

【解析】解：第题：


；



；
第题：由数轴可得：，
，，，
故答案为：，，；
，，，



．
第题：利用二次根式的乘法的法则进行运算即可；
利用二次根式的乘法的法则进行运算即可；
第题：由数轴可得，
利用所得的条件进行求解即可；
结合及绝对值进行运算即可．
本题主要考查二次根式的混合运算，数轴，绝对值，解答的关键是对相应的知识的掌握与运用．
 

21.【答案】第题：解：设辆大货车一次可以运货吨，辆小货车一次可以运货吨，
依题意得：，
解得：，
．
答：辆大货车与辆小货车一次可以运货．
第题：解：设种头盔购进了个，种头盔购进了个，
依题意得：，
解得：．
答：种头盔购进了个，种头盔购进了个．
设该商店第二次购进种头盔个，则购进种头盔个，
依题意得：，
解得：，
又，均为整数，
的最小值为．
答：该商店第二次至少应购进种头盔个． 

【解析】第题：设辆大货车一次可以运货吨，辆小货车一次可以运货吨，根据“辆大货车与辆小货车一次可以运货，辆大货车与辆小货车一次可以运货”，即可得出关于，的二元一次方程组，解之即可得出，的值，再将其代入中即可得出结论；
第题：设种头盔购进了个，种头盔购进了个，根据购进，两种头盔共个，且共用去元钱，即可得出关于，的二元一次方程组，解之即可得出结论；
设该商店第二次购进种头盔个，则购进种头盔个，根据这两次购进的头盔售完后所获总利润不低于元，即可得出关于的一元一次不等式，解之取其中的最小值即可得出结论．
本题考查了二元一次方程组的应用以及一元一次不等式的应用，解题的关键是：第题：找准等量关系，正确列出二元一次方程组；第题：找准等量关系，正确列出二元一次方程组；根据各数量之间的关系，正确列出一元一次不等式．
 

22.【答案】 

【解析】证明：第题：
，，
，，
，
解：第题：

过点作，
则，
，，
；

过点作，
则，
，，
；
当点在的下方时：
，，
，．
．
当点在的上方时：
有：，
；
所以与相等或互补．
第题：利用平行线的性质进行角的等量代换；
第题：先作辅助线，再利用平行线的性质求解；
先作辅助线，再利用平行线的性质求解；
先作辅助线，再利用平行线的性质分类求解．
本题考查了平行线的性质，添加平行线是解题的关键．