初中数学沪科版七年级上册第3章 一次方程与方程组3.3二元一次方程组及其解法教学课件ppt

这是一份初中数学沪科版七年级上册第3章 一次方程与方程组3.3二元一次方程组及其解法教学课件ppt，共18页。PPT课件主要包含了x²1y4，课堂练习等内容，欢迎下载使用。

1.了解二元一次方程及相关概念.2.理解二元一次方程的解及二元一次方程组的解的概念.3.会判断一组数是不是二元一次方程组的解.
篮球联赛中，每场比赛都要分出胜负，每队胜1场得2分，负1场得1分，某队在全部22场比赛中得到40分，那么这个队胜负场数应分别是多少？ 你会用你学过的一元一次方程解决这个问题吗？  
解：设胜x场，则负(22-x)场. 根据题意列式，得 2x+(22-x)=40.
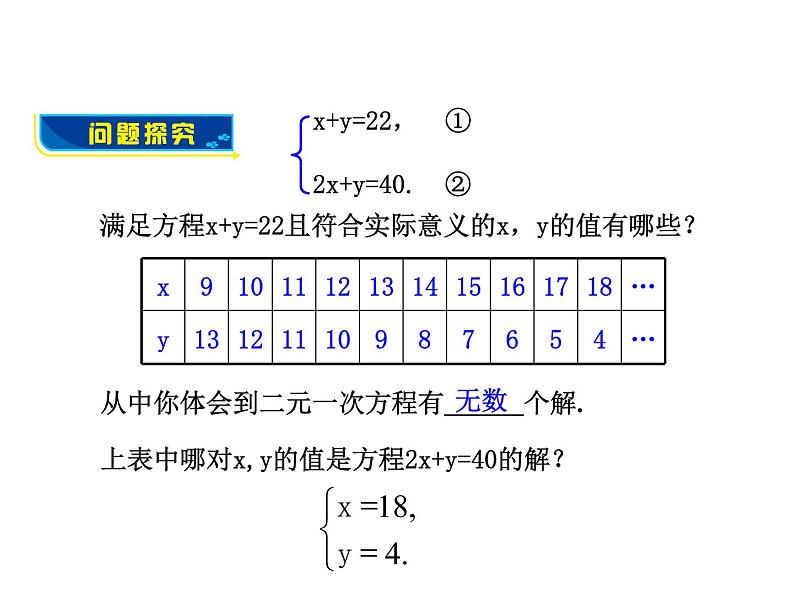
解：设胜x场，负y场,则 x+y=22， ① 2x+y=40. ②
方程中有哪些条件？设胜的场数是x，负的场数为y，你能用方程把这些条件表示出来吗？
含有两个未知数（x和y），并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程.
x+y=22， ① 2x+y=40. ②在未知数的个数和次数上与方程2x+(22-x)=40有什么不一样？
把两个二元一次方程合在一起，就组成了一个二元一次方程组.要点:（1）方程组中只有两个未知数.　　 （2）未知数的次数都是一次.
　　x +y=22， ① 2x + y =40. ②
2.若x(m-3)-8y(n+2)=0 是关于x,y的二元一次方程,则m=____,n=_______.
1.下列各式中是二元一次方程的是( ) A.3x-2y=9 B.2x+y=6z C. +2=3y D.x-3=4y2
选A. 【解析】因为方程2x+y=6z 含有3个未知数，所以不是二元一次方程；因为方程 不是整式方程，所以不是二元一次方程；因为方程x-3=4y2其未知数的最高次数为2.所以不是二元一次方程.故选A.
3.下列方程组中是二元一次方程组的是________.
3x-y=0，y=2x+1.
5x-y=0，3x+z=1.
x+y=3，xy+3=1.
满足方程x+y=22且符合实际意义的x，y的值有哪些？
上表中哪对x,y的值是方程2x+y=40的解？
从中你体会到二元一次方程有＿＿＿个解.
一般地，使二元一次方程组中每个方程都成立的两个未知数的值，叫做二元一次方程组的解.
【例】检验下列各对数是不是方程组 的解.
解:(1)把x=2,y=1分别代入方程①,②,发现不满足②,所以 不是原方程组的解; (2)把x=3，y=-1代入方程①,②,发现不满足①,所以 不是原方程组的解；
1.二元一次方程x-2y=1有无数多个解，下列四组值中不是该方程的解的是( )B 【解析】将各选项逐一代入，其中不能满足方程x-2y=1的是选项B.
2.已知2x+3y=4，当x=y 时，x，y的值为_____，当x+y=0时, x=_____，y=______.3.若方程2x2m+3+3y3n-7=0是关于x,y的二元一次方程，则m=______，n=______.
4.已知 是方程2x-ay=3的一个解，那么a的值是( ) A.1 B.3 C.-3 D.-1
D 【解析】使3x+2y=11成立的x，y有无数组.
1.关于二元一次方程3x+2y=11的解的说法正确的是 ( )A.任何一对有理数都是它的解B.只有一个解C.只有两个解 D.无穷多个解
2. 方程组 的解是( )A． B． C． D．
D 【解析】把 代入方程组 成立.
答案：1【解析】根据二元一次方程的定义，得|m|=1且m+1≠0， 解得m=1.
3.已知(m+1)x|m|+y=0是关于x，y的二元一次方程，则m=_______.
4.若 是方程 - -k=0的解，则k值为( )A.B.C.D.
B 【解析】根据题意把s,t的值代入方程可得到所以k = .