2022年河北省辛集市达标名校中考一模数学试题含解析

这是一份2022年河北省辛集市达标名校中考一模数学试题含解析，共21页。试卷主要包含了考生要认真填写考场号和座位序号，计算的结果是等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
注意事项
1．考生要认真填写考场号和座位序号。
2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。
3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1．在一次中学生田径运动会上，参加跳远的名运动员的成绩如下表所示:
成绩（米）






人数






则这名运动员成绩的中位数、众数分别是（ ）
A． B． C．， D．
2．如果代数式有意义，则实数x的取值范围是（ ）
A．x≥﹣3 B．x≠0 C．x≥﹣3且x≠0 D．x≥3
3．2017上半年，四川货物贸易进出口总值为2 098.7亿元，较去年同期增长59.5%，远高于同期全国19.6%的整体进出口增幅．在“一带一路”倡议下，四川同期对以色列、埃及、罗马尼亚、伊拉克进出口均实现数倍增长．将2098.7亿元用科学记数法表示是（　　）
A．2.098 7×103 B．2.098 7×1010 C．2.098 7×1011 D．2.098 7×1012
4．小丽只带2元和5元的两种面额的钞票（数量足够多），她要买27元的商品，而商店不找零钱，要她刚好付27元，她的付款方式有（ ）种．
A．1 B．2 C．3 D．4
5．某学校组织艺术摄影展，上交的作品要求如下：七寸照片（长7英寸，宽5英寸）；将照片贴在一张矩形衬纸的正中央，照片四周外露衬纸的宽度相同；矩形衬纸的面积为照片面积的3倍．设照片四周外露衬纸的宽度为x英寸（如图），下面所列方程正确的是（　　）

A．（7+x）（5+x）×3=7×5 B．（7+x）（5+x）=3×7×5
C．（7+2x）（5+2x）×3=7×5 D．（7+2x）（5+2x）=3×7×5
6．把8a3﹣8a2+2a进行因式分解，结果正确的是（ ）
A．2a（4a2﹣4a+1） B．8a2（a﹣1） C．2a（2a﹣1）2 D．2a（2a+1）2
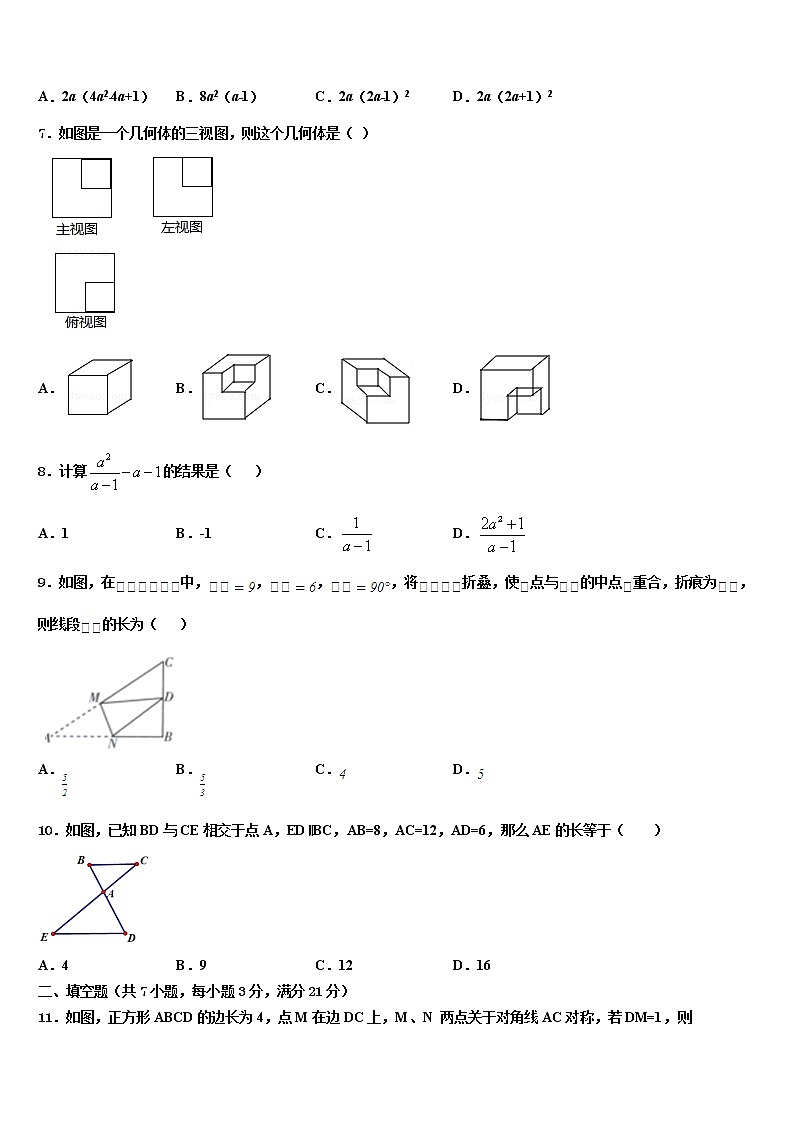
7．如图是一个几何体的三视图，则这个几何体是（ ）

A． B． C． D．
8．计算的结果是（ ）
A．1 B．-1 C． D．
9．如图，在中，，，，将折叠，使点与的中点重合，折痕为，则线段的长为（ ）

A． B． C． D．
10．如图，已知BD与CE相交于点A，ED∥BC，AB=8，AC=12，AD=6，那么AE的长等于（ ）

A．4 B．9 C．12 D．16
二、填空题（共7小题，每小题3分，满分21分）
11．如图，正方形ABCD的边长为4，点M在边DC上，M、N 两点关于对角线AC对称，若DM=1，则tan∠ADN= ．

12．若点（a，b）在一次函数y=2x-3的图象上，则代数式4a-2b-3的值是__________
13．分式方程=1的解为_____
14．已知a2+a=1，则代数式3﹣a﹣a2的值为_____．
15．某校“百变魔方”社团为组织同学们参加学校科技节的“最强大脑”大赛，准备购买A，B两款魔方.社长发现若购买2个A款魔方和6个B款魔方共需170元，购买3个A款魔方和购买8个B款魔方所需费用相同. 求每款魔方的单价.设A款魔方的单价为x元，B款魔方的单价为y元，依题意可列方程组为_______.
16．分解因式：m2n﹣2mn+n= ．
17．如果将“概率”的英文单词 probability中的11个字母分别写在11张相同的卡片上，字面朝下随意放在桌子上，任取一张，那么取到字母b的概率是________．
三、解答题（共7小题，满分69分）
18．（10分）庐阳春风体育运动品商店从厂家购进甲，乙两种T恤共400件，其每件的售价与进货量（件）之间的关系及成本如下表所示：
T恤
每件的售价/元
每件的成本/元
甲

50
乙

60

（1）当甲种T恤进货250件时，求两种T恤全部售完的利润是多少元；若所有的T恤都能售完，求该商店获得的总利润（元）与乙种T恤的进货量（件）之间的函数关系式；在（2）的条件下，已知两种T恤进货量都不低于100件，且所进的T恤全部售完，该商店如何安排进货才能使获得的利润最大？
19．（5分）在△ABC中，已知AB=AC，∠BAC=90°，E为边AC上一点，连接BE．
(1)如图1，若∠ABE=15°，O为BE中点，连接AO，且AO=1，求BC的长；
(2)如图2，D为AB上一点，且满足AE=AD，过点A作AF⊥BE交BC于点F，过点F作FG⊥CD交BE的延长线于点G，交AC于点M，求证：BG=AF+FG．

20．（8分）某数学兴趣小组为测量如图（①所示的一段古城墙的高度，设计用平面镜测量的示意图如图②所示，点P处放一水平的平面镜，光线从点A出发经过平面镜反射后刚好射到古城墙CD的顶端C处．
已知AB⊥BD、CD⊥BD，且测得AB=1.2m，BP=1.8m.PD=12m，求该城墙的高度（平面镜的原度忽略不计）： 请你设计一个测量这段古城墙高度的方案．
要求：①面出示意图（不要求写画法）；②写出方案，给出简要的计算过程：③给出的方案不能用到图②的方法．
21．（10分）已知：如图，在平面直角坐标系中，O为坐标原点，△OAB的顶点A、B的坐标分别是A（0，5），B（3，1），过点B画BC⊥AB交直线于点C，连结AC，以点A为圆心，AC为半径画弧交x轴负半轴于点D，连结AD、CD．
（1）求证：△ABC≌△AOD．
（2）设△ACD的面积为，求关于的函数关系式．
（3）若四边形ABCD恰有一组对边平行，求的值．

22．（10分）如图，Rt△ABC中，∠ABC＝90°，点D，F分别是AC，AB的中点，CE∥DB，BE∥DC．
(1)求证：四边形DBEC是菱形；
(2)若AD＝3， DF＝1，求四边形DBEC面积．

23．（12分）问题提出
（1）如图①，在矩形ABCD中，AB=2AD，E为CD的中点，则∠AEB　 　∠ACB（填“＞”“＜”“=”）；
问题探究
（2）如图②，在正方形ABCD中，P为CD边上的一个动点，当点P位于何处时，∠APB最大？并说明理由；
问题解决
（3）如图③，在一幢大楼AD上装有一块矩形广告牌，其侧面上、下边沿相距6米（即AB=6米），下边沿到地面的距离BD=11.6米．如果小刚的睛睛距离地面的高度EF为1.6米，他从远处正对广告牌走近时，在P处看广告效果最好（视角最大），请你在图③中找到点P的位置，并计算此时小刚与大楼AD之间的距离．

24．（14分）“低碳生活，绿色出行”是我们倡导的一种生活方式，有关部门抽样调查了某单位员工上下班的交通方式，绘制了如下统计图：

（1）填空：样本中的总人数为 ；开私家车的人数m= ；扇形统计图中“骑自行车”所在扇形的圆心角为 度；
（2）补全条形统计图；
（3）该单位共有2000人，积极践行这种生活方式，越来越多的人上下班由开私家车改为骑自行车．若步行，坐公交车上下班的人数保持不变，问原来开私家车的人中至少有多少人改为骑自行车，才能使骑自行车的人数不低于开私家车的人数？



参考答案

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1、D
【解析】
根据中位数、众数的定义即可解决问题．
【详解】
解：这些运动员成绩的中位数、众数分别是4.70，4.1．
故选：D．
【点睛】
本题考查中位数、众数的定义，解题的关键是记住中位数、众数的定义，属于中考基础题.
2、C
【解析】
根据二次根式有意义和分式有意义的条件列出不等式，解不等式即可．
【详解】
由题意得，x+3≥0，x≠0，
解得x≥−3且x≠0，
故选C.
【点睛】
本题考查分式有意义条件，二次根式有意义的条件，熟练掌握相关知识是解题的关键.
3、C
【解析】
将2098.7亿元用科学记数法表示是2.0987×1011，
故选：C．
点睛: 本题考查了正整数指数科学计数法,对于一个绝对值较大的数，用科学记数法写成 的形式，其中，n是比原整数位数少1的数.
4、C
【解析】
分析：先根据题意列出二元一次方程，再根据x，y都是非负整数可求得x，y的值．
详解：解：设2元的共有x张，5元的共有y张，
由题意，2x+5y=27
∴x=（27-5y）
∵x，y是非负整数，
∴或或，
∴付款的方式共有3种．
故选C.
点睛：本题考查二元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再根据实际意义求解．
5、D
【解析】
试题分析：由题意得；如图知；矩形的长="7+2x" 宽=5+2x ∴矩形衬底的面积=3倍的照片的面积，可得方程为(7+2X)(5+2X)=3×7×5
考点：列方程
点评：找到题中的等量关系，根据两个矩形的面积3倍的关系得到方程，注意的是矩形的间距都为等量的，从而得到大矩形的长于宽，用未知数x的代数式表示，而列出方程，属于基础题．
6、C
【解析】
首先提取公因式2a，进而利用完全平方公式分解因式即可．
【详解】
解：8a3﹣8a2+2a
=2a(4a2﹣4a+1)
=2a(2a﹣1)2，故选C.
【点睛】
本题因式分解中提公因式法与公式法的综合运用.
7、B
【解析】
试题分析：结合三个视图发现，应该是由一个正方体在一个角上挖去一个小正方体，且小正方体的位置应该在右上角，故选B．
考点：由三视图判断几何体．
8、C
【解析】
原式通分并利用同分母分式的减法法则计算，即可得到结果．
【详解】
解：==，
故选：C.
【点睛】
此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．
9、C
【解析】
设BN=x，则由折叠的性质可得DN=AN=9-x，根据中点的定义可得BD=3，在Rt△BND中，根据勾股定理可得关于x的方程，解方程即可求解．
【详解】
设，则.
由折叠的性质，得.
因为点是的中点，
所以.
在中，
由勾股定理，得，
即，
解得，
故线段的长为4.
故选C.
【点睛】
此题考查了折叠的性质，勾股定理，中点的定义以及方程思想，熟练掌握折叠的性质及勾股定理是解答本题的关键．
10、B
【解析】
由于ED∥BC，可证得△ABC∽△ADE，根据相似三角形所得比例线段，即可求得AE的长．
【详解】
∵ED∥BC，
∴△ABC∽△ADE，
∴ =，
∴ ==，
即AE=9；
∴AE=9.
故答案选B.
【点睛】
本题考查的知识点是相似三角形的判定与性质，解题的关键是熟练的掌握相似三角形的判定与性质.

二、填空题（共7小题，每小题3分，满分21分）
11、
【解析】
M、N两点关于对角线AC对称，所以CM=CN，进而求出CN的长度．再利用∠ADN=∠DNC即可求得tan∠ADN．
【详解】
解：在正方形ABCD中，BC=CD=1．
∵DM=1，
∴CM=2，
∵M、N两点关于对角线AC对称，
∴CN=CM=2．
∵AD∥BC，
∴∠ADN=∠DNC，


故答案为
【点睛】
本题综合考查了正方形的性质，轴对称的性质以及锐角三角函数的定义．
12、1
【解析】
根据题意，将点（a，b）代入函数解析式即可求得2a-b的值，变形即可求得所求式子的值．
【详解】
∵点（a，b）在一次函数y=2x-1的图象上，
∴b=2a-1，
∴2a-b=1，
∴4a-2b=6，
∴4a-2b-1=6-1=1，
故答案为：1．
【点睛】
本题考查一次函数图象上点的坐标特征，解答本题的关键是明确题意，利用一次函数的性质解答．
13、x=0.1
【解析】
分析：方程两边都乘以最简公分母，化为整式方程，然后解方程，再进行检验．
详解：方程两边都乘以2（x2﹣1）得，
8x+2﹣1x﹣1=2x2﹣2，
解得x1=1，x2=0.1，
检验：当x=0.1时，x﹣1=0.1﹣1=﹣0.1≠0，
当x=1时，x﹣1=0，
所以x=0.1是方程的解，
故原分式方程的解是x=0.1．
故答案为：x=0.1
点睛：本题考查了解分式方程，（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．（2）解分式方程一定注意要验根．
14、2
【解析】
∵，
∴，
故答案为2.
15、
【解析】
分析：设A款魔方的单价为x元，B魔方单价为y元，根据“购买两个A款魔方和6个B款魔方共需170元，购买3个A款魔方和购买8个B款魔方所需费用相同”，即可得出关于x,y的二元一次方程组，此题得解．
解：设A魔方的单价为x元，B款魔方的单价为y元，根据题意得：
故答案为
点睛：本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键．
16、n（m﹣1）1．
【解析】
先提取公因式n后，再利用完全平方公式分解即可
【详解】
m1n﹣1mn+n=n（m1﹣1m+1）=n（m﹣1）1．
故答案为n（m﹣1）1．
17、
【解析】
分析：让英文单词probability中字母b的个数除以字母的总个数即为所求的概率．
详解：∵英文单词probability中，一共有11个字母，其中字母b有2个，∴任取一张，那么取到字母b的概率为．
故答案为．
点睛：本题考查了概率公式，用到的知识点为：概率等于所求情况数与总情况数之比．

三、解答题（共7小题，满分69分）
18、（1）10750；（2）；（3）最大利润为10750元.
【解析】
（1）根据“利润=销售总额-总成本”结合两种T恤的销售数量代入相关代数式进行求解即可；
（2）根据题意，分两种情况进行讨论：①0 （3）求出（2）中各函数最大值，进行比较即可得到结论.
【详解】
（1）∵甲种T恤进货250件
∴乙种T恤进货量为：400-250=150件
故由题意得，；
（2）①
②；
故.
（3）由题意，，①，，
②，
综上，最大利润为10750元.
【点睛】
本题考查了二次函数的应用，找出题中的等量关系以及根据题意确定二次函数的解析式是解题的关键．
19、（1） （2）证明见解析
【解析】
（1）如图1中，在AB上取一点M，使得BM=ME，连接ME．，设AE=x，则ME=BM=2x，AM=x，根据AB2+AE2=BE2，可得方程（2x+x）2+x2=22，解方程即可解决问题．
（2）如图2中，作CQ⊥AC，交AF的延长线于Q，首先证明EG=MG，再证明FM=FQ即可解决问题．
【详解】
解：如图 1 中，在 AB 上取一点 M，使得 BM=ME，连接 ME．
在 Rt△ABE 中，∵OB=OE，
∴BE=2OA=2，
∵MB=ME，
∴∠MBE=∠MEB=15°，
∴∠AME=∠MBE+∠MEB=30°，设 AE=x，则 ME=BM=2x，AM=x，
∵AB2+AE2=BE2，
∴，
∴x= （负根已经舍弃），
∴AB=AC=（2+ ）• ，
∴BC= AB= +1．
作 CQ⊥AC，交 AF 的延长线于 Q，

∵ AD=AE ，AB=AC ，∠BAE=∠CAD，
∴△ABE≌△ACD（SAS），
∴∠ABE=∠ACD，
∵∠BAC=90°，FG⊥CD，
∴∠AEB=∠CMF，
∴∠GEM=∠GME，
∴EG=MG，
∵∠ABE=∠CAQ，AB=AC，∠BAE=∠ACQ=90°，
∴△ABE≌△CAQ（ASA），
∴BE=AQ，∠AEB=∠Q，
∴∠CMF=∠Q，
∵∠MCF=∠QCF=45°，CF=CF，
∴△CMF≌△CQF（AAS），
∴FM=FQ，
∴BE=AQ=AF+FQ=AF=FM，
∵EG=MG，
∴BG=BE+EG=AF+FM+MG=AF+FG．
【点睛】
本题考查全等三角形的判定和性质、直角三角形斜边中线定理，等腰直角三角形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．
20、（1）8m；（2）答案不唯一
【解析】
（1）根据入射角等于反射角可得 ∠APB=∠CPD ，由 AB⊥BD、CD⊥BD 可得到 ∠ABP=∠CDP=90°，从而可证得三角形相似，根据相似三角形的性质列出比例式，即可求出CD的长.
（2）设计成视角问题求古城墙的高度.
【详解】
（1）解：由题意，得∠APB=∠CPD，∠ABP=∠CDP=90°，
∴Rt△ABP∽Rt△CDP，
∴ ，
∴CD==8.
答：该古城墙的高度为8m
（2）解：答案不唯一，如：如图，

在距这段古城墙底部am的E处，用高h（m）的测角仪DE测得这段古城墙顶端A的仰角为α.即可测量这段古城墙AB的高度，
过点D作DCAB于点C.在Rt△ACD中，∠ACD=90°，tanα=，
∴AC=α tanα，
∴AB=AC+BC=αtanα+h
【点睛】
本题考查相似三角形性质的应用．解题时关键是找出相似的三角形，然后根据对应边成比例列出方程，建立适当的数学模型来解决问题．
21、（1）证明详见解析；（2）S=（m+1）2+（m＞）；（2）2或1．
【解析】
试题分析：（1）利用两点间的距离公式计算出AB=5，则AB=OA，则可根据“HL”证明△ABC≌△AOD；
（2）过点B作直线BE⊥直线y=﹣m于E，作AF⊥BE于F，如图，证明Rt△ABF∽Rt△BCE，利用相似比可得BC=（m+1），再在Rt△ACB中，由勾股定理得AC2=AB2+BC2=25+（m+1）2，然后证明△AOB∽△ACD，利用相似的性质得，而S△AOB=，于是可得S=（m+1）2+（m＞）；
（2）作BH⊥y轴于H，如图，分类讨论：当AB∥CD时，则∠ACD=∠CAB，由△AOB∽△ACD得∠ACD=∠AOB，所以∠CAB=∠AOB，利用三角函数得到tan∠AOB=2，tan∠ACB=，所以=2；当AD∥BC，则∠5=∠ACB，由△AOB∽△ACD得到∠4=∠5，则∠ACB=∠4，根据三角函数定义得到tan∠4=，tan∠ACB=，则=，然后分别解关于m的方程即可得到m的值．
试题解析：（1）证明：∵A（0，5），B（2，1），
∴AB==5，
∴AB=OA，
∵AB⊥BC，
∴∠ABC=90°，
在Rt△ABC和Rt△AOD中，
，
∴Rt△ABC≌Rt△AOD；
（2）解：过点B作直线BE⊥直线y=﹣m于E，作AF⊥BE于F，如图，∵∠1+∠2=90°，∠1+∠2=90°，
∴∠2=∠2，
∴Rt△ABF∽Rt△BCE，
∴，即，
∴BC=(m+1），
在Rt△ACB中，AC2=AB2+BC2=25+（m+1）2，
∵△ABC≌△AOD，
∴∠BAC=∠OAD，即∠4+∠OAC=∠OAC+∠5，
∴∠4=∠5，
而AO=AB，AD=AC，
∴△AOB∽△ACD，
∴=，
而S△AOB=×5×2=，
∴S=（m+1）2+（m＞）；
（2）作BH⊥y轴于H，如图，
当AB∥CD时，则∠ACD=∠CAB，
而△AOB∽△ACD，
∴∠ACD=∠AOB，
∴∠CAB=∠AOB，
而tan∠AOB==2，tan∠ACB===，
∴=2，解得m=1；
当AD∥BC，则∠5=∠ACB，
而△AOB∽△ACD，
∴∠4=∠5，
∴∠ACB=∠4，
而tan∠4=，tan∠ACB=，
∴=，
解得m=2．
综上所述，m的值为2或1．

考点：相似形综合题．
22、 (1)见解析;(1)4
【解析】
（1）根据平行四边形的判定定理首先推知四边形DBEC为平行四边形，然后由直角三角形斜边上的中线等于斜边的一半得到其邻边相等：CD=BD，得证；
（1）由三角形中位线定理和勾股定理求得AB边的长度，然后根据菱形的性质和三角形的面积公式进行解答．
【详解】
（1）证明：∵CE∥DB，BE∥DC，
∴四边形DBEC为平行四边形．
又∵Rt△ABC中，∠ABC=90°，点D是AC的中点，
∴CD=BD=AC，
∴平行四边形DBEC是菱形；
（1）∵点D，F分别是AC，AB的中点，AD=3，DF=1，
∴DF是△ABC的中位线，AC=1AD=6，S△BCD=S△ABC
∴BC=1DF=1．
又∵∠ABC=90°，
∴AB= = = 4．
∵平行四边形DBEC是菱形，
∴S四边形DBEC=1S△BCD=S△ABC=AB•BC=×4×1=4．

点睛：本题考查了菱形的判定与性质，直角三角形斜边上的中线等于斜边的一半，三角形中位线定理.由点D是AC的中点，得到CD=BD是解答（1）的关键，由菱形的性质和三角形的面积公式得到S四边形DBEC=S△ABC是解（1）的关键.
23、（1）＞；（2）当点P位于CD的中点时，∠APB最大，理由见解析；（3）4米．
【解析】
（1）过点E作EF⊥AB于点F，由矩形的性质和等腰三角形的判定得到：△AEF是等腰直角三角形，易证∠AEB=90°，而∠ACB＜90°，由此可以比较∠AEB与∠ACB的大小
（2）假设P为CD的中点，作△APB的外接圆⊙O，则此时CD切⊙O于P，在CD上取任意异于P点的点E，连接AE，与⊙O交于点F，连接BE、BF；由∠AFB是△EFB的外角，得∠AFB＞∠AEB，且∠AFB与∠APB均为⊙O中弧AB所对的角，则∠AFB=∠APB，即可判断∠APB与∠AEB的大小关系，即可得点P位于何处时，∠APB最大；
（3）过点E作CE∥DF，交AD于点C，作AB的垂直平分线，垂足为点Q，并在垂直平分线上取点O，使OA=CQ，以点O为圆心，OB为半径作圆，则⊙O切CE于点G，连接OG，并延长交DF于点P，连接OA，再利用勾股定理以及长度关系即可得解.
【详解】
解：（1）∠AEB＞∠ACB，理由如下：

如图1，过点E作EF⊥AB于点F，
∵在矩形ABCD中，AB=2AD，E为CD中点，
∴四边形ADEF是正方形，
∴∠AEF=45°，
同理，∠BEF=45°，
∴∠AEB=90°．
而在直角△ABC中，∠ABC=90°，
∴∠ACB＜90°，
∴∠AEB＞∠ACB．
故答案为：＞；
（2）当点P位于CD的中点时，∠APB最大，理由如下：
假设P为CD的中点，如图2，作△APB的外接圆⊙O，则此时CD切⊙O于点P，

在CD上取任意异于P点的点E，连接AE，与⊙O交于点F，连接BE，BF，
∵∠AFB是△EFB的外角，
∴∠AFB＞∠AEB，
∵∠AFB=∠APB，
∴∠APB＞∠AEB，
故点P位于CD的中点时，∠APB最大：
（3）如图3，过点E作CE∥DF交AD于点C，作线段AB的垂直平分线，垂足为点Q，并在垂直平分线上取点O，使OA=CQ，

以点O为圆心，OA长为半径作圆，则⊙O切CE于点G，连接OG，并延长交DF于点P，此时点P即为小刚所站的位置，
由题意知DP=OQ=，
∵OA=CQ=BD+QB﹣CD=BD+AB﹣CD，
BD=11.6米， AB=3米，CD=EF=1.6米，
∴OA=11.6+3﹣1.6=13米，
∴DP=米，
即小刚与大楼AD之间的距离为4米时看广告牌效果最好．
【点睛】
本题考查了矩形的性质，正方形的判定与性质，圆周角定理的推论，三角形外角的性质，线段垂直平分线的性质，勾股定理等知识，难度较大，熟练掌握各知识点并正确作出辅助圆是解答本题的关键.
24、（1）80，20，72；（2）16，补图见解析；（3）原来开私家车的人中至少有50人改为骑自行车，才能使骑自行车的人数不低于开私家车的人数．
【解析】
试题分析：（1）用乘公交车的人数除以所占的百分比，计算即可求出总人数，再用总人数乘以开私家车的所占的百分比求出m，用360°乘以骑自行车的所占的百分比计算即可得解：
样本中的总人数为：36÷45%=80人；
开私家车的人数m=80×25%=20；
扇形统计图中“骑自行车”的圆心角为.
（2）求出骑自行车的人数，然后补全统计图即可.
（3）设原来开私家车的人中有x人改为骑自行车，表示出改后骑自行车的人数和开私家车的人数，列式不等式，求解即可．
试题解析：解：（1）80，20，72.
（2）骑自行车的人数为：80×20%=16人，
补全统计图如图所示；

（3）设原来开私家车的人中有x人改为骑自行车，
由题意得，，解得x≥50.
答：原来开私家车的人中至少有50人改为骑自行车，才能使骑自行车的人数不低于开私家车的人数．
考点：1.条形统计图；2.扇形统计图；3.频数、频率和总量的关系；4.一元一次不等式的应用．