贵州省贵阳市2020-2022中考数学真题分类汇编-02填空题知识点分类

贵州省贵阳市2020-2022中考数学真题分类汇编-02填空题知识点分类

一．单项式乘多项式

1．（2020•贵阳）化简x（x﹣1）+x的结果是　   　．

二．因式分解-提公因式法

2．（2022•贵阳）因式分解：a2+2a＝　   　．

三．方程的定义

3．（2022•贵阳）“方程”二字最早见于我国《九章算术》这部经典著作中，该书的第八章名为“方程”．如：从左到右列出的算筹数分别表示方程中未知数x，y的系数与相应的常数项，即可表示方程x+4y＝23，则表示的方程是 　   　．

四．反比例函数系数k的几何意义

4．（2020•贵阳）如图，点A是反比例函数y＝图象上任意一点，过点A分别作x轴，y轴的垂线，垂足为B，C，则四边形OBAC的面积为　   　．

五．二次函数的性质

5．（2021•贵阳）二次函数y＝x2的图象开口方向是 　   　（填“向上”或“向下”）．

六．全等三角形的判定与性质

6．（2021•贵阳）在综合实践课上，老师要求同学用正方形纸片剪出正三角形且正三角形的顶点都在正方形边上．小红利用两张边长为2的正方形纸片，按要求剪出了一个面积最大的正三角形和一个面积最小的正三角形．则这两个正三角形的边长分别是 　   　．

七．勾股定理

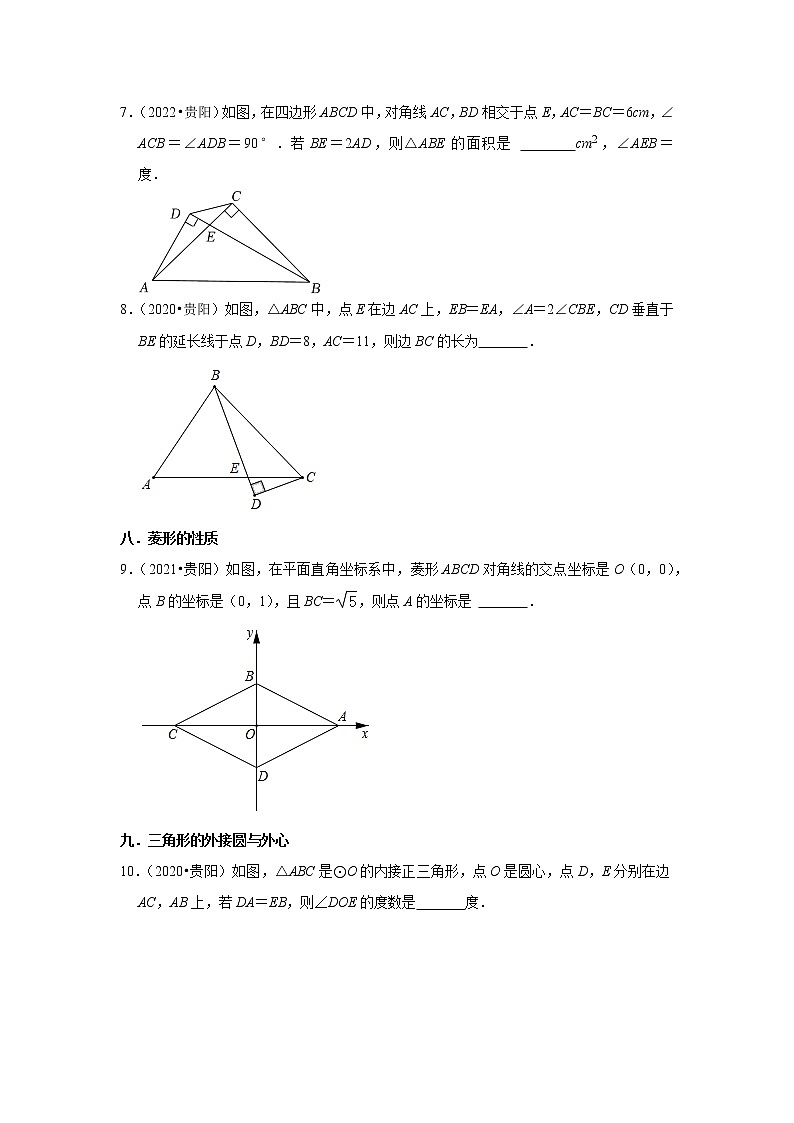
7．（2022•贵阳）如图，在四边形ABCD中，对角线AC，BD相交于点E，AC＝BC＝6cm，∠ACB＝∠ADB＝90°．若BE＝2AD，则△ABE的面积是 　   　cm2，∠AEB＝　   　度．

8．（2020•贵阳）如图，△ABC中，点E在边AC上，EB＝EA，∠A＝2∠CBE，CD垂直于BE的延长线于点D，BD＝8，AC＝11，则边BC的长为　   　．

八．菱形的性质

9．（2021•贵阳）如图，在平面直角坐标系中，菱形ABCD对角线的交点坐标是O（0，0），点B的坐标是（0，1），且BC＝，则点A的坐标是 　   　．

九．三角形的外接圆与外心

10．（2020•贵阳）如图，△ABC是⊙O的内接正三角形，点O是圆心，点D，E分别在边AC，AB上，若DA＝EB，则∠DOE的度数是　   　度．

一十．概率公式

11．（2022•贵阳）端午节到了，小红煮好了10个粽子，其中有6个红枣粽子，4个绿豆粽子．小红想从煮好的粽子中随机捞一个，若每个粽子形状完全相同，被捞到的机会相等，则她捞到红枣粽子的概率是 　   　．

一十一．列表法与树状图法

12．（2021•贵阳）贵阳市2021年中考物理实验操作技能测试中，要求学生两人一组合作进行，并随机抽签决定分组．有甲、乙、丙、丁四位同学参加测试，则甲、乙两位同学分到同一组的概率是 　   　．

一十二．利用频率估计概率

13．（2020•贵阳）在“抛掷正六面体”的试验中，正六面体的六个面分别标有数字“1”“2”“3”“4”“5”“6”，在试验次数很大时，数字“6”朝上的频率稳定在　   　．

参考答案与试题解析

一．单项式乘多项式

1．（2020•贵阳）化简x（x﹣1）+x的结果是　x2　．

【解答】解：x（x﹣1）+x

＝x2﹣x+x

＝x2，

故答案为：x2．

二．因式分解-提公因式法

2．（2022•贵阳）因式分解：a2+2a＝　a（a+2）　．

【解答】解：a2+2a＝a（a+2）．

故答案为：a（a+2）．

三．方程的定义

3．（2022•贵阳）“方程”二字最早见于我国《九章算术》这部经典著作中，该书的第八章名为“方程”．如：从左到右列出的算筹数分别表示方程中未知数x，y的系数与相应的常数项，即可表示方程x+4y＝23，则表示的方程是 　x+2y＝32　．

【解答】解：根据题知：从左到右列出的算筹数分别表示方程中未知数x，y的系数与相应的常数项，

一个竖线表示一个，一条横线表示一十，

所以该图表示的方程是：x+2y＝32．

四．反比例函数系数k的几何意义

4．（2020•贵阳）如图，点A是反比例函数y＝图象上任意一点，过点A分别作x轴，y轴的垂线，垂足为B，C，则四边形OBAC的面积为　3　．

【解答】解：∵过点A分别作x轴，y轴的垂线，垂足为B，C，

∴AB×AC＝|k|＝3，

则四边形OBAC的面积为：3．

故答案为：3．

五．二次函数的性质

5．（2021•贵阳）二次函数y＝x2的图象开口方向是 　向上　（填“向上”或“向下”）．

【解答】解：由y＝x2得：a＞0，

∴二次函数图象开口向上．

故答案为：向上．

六．全等三角形的判定与性质

6．（2021•贵阳）在综合实践课上，老师要求同学用正方形纸片剪出正三角形且正三角形的顶点都在正方形边上．小红利用两张边长为2的正方形纸片，按要求剪出了一个面积最大的正三角形和一个面积最小的正三角形．则这两个正三角形的边长分别是 　2﹣2，2　．

【解答】解：如图，设△GEF为正方形ABCD的一个内接正三角形，

作正△GEF的高EK，连接KA，KD，

∵∠EKG＝∠EDG＝90°，

∴E、K、D、G四点共圆，

∴∠KDE＝∠KGE＝60°，

同理∠KAE＝60°，

∴△KAD是一个正三角形，

则K必为一个定点，

∵正三角形面积取决于它的边长，

∴当FG⊥AB时，边长FG最小，面积也最小，此时边长等于正方形边长为2，

当FG过B点时，即F'与点B重合时，边长最大，面积也最大，

此时作KH⊥BC于H，

由等边三角形的性质可知，

K为FG的中点，

∵KH∥CD，

∴KH为三角形F'CG'的中位线，

∴CG'＝2HK＝2（EH﹣EK）＝2（2﹣2×sin60°）＝4﹣2，

∴F'G'＝＝＝＝2﹣2，

故答案为：2﹣2，2．

七．勾股定理

7．（2022•贵阳）如图，在四边形ABCD中，对角线AC，BD相交于点E，AC＝BC＝6cm，∠ACB＝∠ADB＝90°．若BE＝2AD，则△ABE的面积是 　36﹣18　cm2，∠AEB＝　112.5　度．

【解答】解：过E作EH⊥AB于H，如图：

设AD＝xcm，CE＝ycm，则BE＝2xcm，AE＝（6﹣y）cm，

∵∠ADB＝∠ACB＝90°，∠AED＝∠CEB，

∴△AED∽△BEC，

∴＝，即＝，

∴x2＝18﹣3y①，

在Rt△BCE中，BC2+CE2＝BE2，

∴62+y2＝（2x）2②，

由①②得y＝6﹣6（负值已舍去），

∴CE＝（6﹣6）cm，AE＝（12﹣6）cm，

∴S△ABE＝S△ABC﹣S△BCE＝×6×6﹣×6×（6﹣6）＝（36﹣18）cm2，

∵AC＝BC＝6，∠ACB＝90°，

∴∠CAB＝45°，AB＝6cm，

∴△AEH是等腰直角三角形，

∴∠AEH＝45°，AH＝＝＝（6﹣6）cm，

∴∠CEH＝180°﹣∠AEH＝135°，BH＝AB﹣AH＝6﹣（6﹣6）＝6cm，

∴BH＝6cm＝BC，

又BE＝BE，∠BCE＝90°＝∠BHE，

∴Rt△BCE≌Rt△BHE（HL），

∴∠BEH＝∠BEC＝∠CEH＝67.5°，

∴∠AEB＝∠AEH+∠BEH＝45°+67.5°＝112.5°，

故答案为：36﹣18，112.5．

8．（2020•贵阳）如图，△ABC中，点E在边AC上，EB＝EA，∠A＝2∠CBE，CD垂直于BE的延长线于点D，BD＝8，AC＝11，则边BC的长为　4　．

【解答】解：延长BD到F，使得DF＝BD，

∵CD⊥BF，

∴△BCF是等腰三角形，

∴BC＝CF，

过点C作CH∥AB，交BF于点H

∴∠ABD＝∠CHD＝2∠CBD＝2∠F，

∴HF＝HC，

∵CH∥AB，

∴∠ABE＝∠CHE，∠BAE＝∠ECH，

∴EH＝CE，

∵EA＝EB，

∴AC＝BH，

∵BD＝8，AC＝11，

∴DH＝BH﹣BD＝AC﹣BD＝3，

∴HF＝HC＝8﹣3＝5，

在Rt△CDH，

∴由勾股定理可知：CD＝4，

在Rt△BCD中，

∴BC＝＝4，

故答案为：4

八．菱形的性质

9．（2021•贵阳）如图，在平面直角坐标系中，菱形ABCD对角线的交点坐标是O（0，0），点B的坐标是（0，1），且BC＝，则点A的坐标是 　（2，0）　．

【解答】解：∵四边形ABCD是菱形，

∴∠BOC＝90°，OC＝OA，

∵点B的坐标是（0，1），

∴OB＝1，

在直角三角形BOC中，BC＝，

∴OC＝＝2，

∴点C的坐标（﹣2，0），

∵点A与点C关于原点对称，

∴点A的坐标（2，0）．

故答案为：（2，0）．

九．三角形的外接圆与外心

10．（2020•贵阳）如图，△ABC是⊙O的内接正三角形，点O是圆心，点D，E分别在边AC，AB上，若DA＝EB，则∠DOE的度数是　120　度．

【解答】解：连接OA，OB，

∵△ABC是⊙O的内接正三角形，

∴∠AOB＝120°，

∵OA＝OB，

∴∠OAB＝∠OBA＝30°，

∵∠CAB＝60°，

∴∠OAD＝30°，

∴∠OAD＝∠OBE，

∵AD＝BE，

∴△OAD≌△OBE（SAS），

∴∠DOA＝∠BOE，

∴∠DOE＝∠DOA+∠AOE＝∠AOE+∠BOE＝∠AOB＝120°，

故答案为：120．

一十．概率公式

11．（2022•贵阳）端午节到了，小红煮好了10个粽子，其中有6个红枣粽子，4个绿豆粽子．小红想从煮好的粽子中随机捞一个，若每个粽子形状完全相同，被捞到的机会相等，则她捞到红枣粽子的概率是 　　．

【解答】解：∵共10个粽子，其中有6个红枣粽子，4个绿豆粽子，

∴P（捞到红枣馅粽子）＝＝，

故答案为：．

一十一．列表法与树状图法

12．（2021•贵阳）贵阳市2021年中考物理实验操作技能测试中，要求学生两人一组合作进行，并随机抽签决定分组．有甲、乙、丙、丁四位同学参加测试，则甲、乙两位同学分到同一组的概率是 　　．

【解答】解：画树状图如图：

共有12种等可能的结果，甲、乙两位同学分到同一组的结果有4种，

∴甲、乙两位同学分到同一组的概率为＝，

故答案为：．

一十二．利用频率估计概率

13．（2020•贵阳）在“抛掷正六面体”的试验中，正六面体的六个面分别标有数字“1”“2”“3”“4”“5”“6”，在试验次数很大时，数字“6”朝上的频率稳定在　　．

【解答】解：在试验次数很大时，数字“6”朝上的频率的变化趋势接近的值是．

故答案为：．