2022届内蒙古根河市阿龙山中学中考押题数学预测卷含解析

这是一份2022届内蒙古根河市阿龙山中学中考押题数学预测卷含解析，共22页。试卷主要包含了答题时请按要求用笔，下列计算正确的是，下列实数中，最小的数是，计算3–等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
注意事项:
1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1．按如下方法，将△ABC的三边缩小的原来的，如图，任取一点O，连AO、BO、CO，并取它们的中点D、E、F，得△DEF，则下列说法正确的个数是（　　）
①△ABC与△DEF是位似图形      ②△ABC与△DEF是相似图形
③△ABC与△DEF的周长比为1：2   ④△ABC与△DEF的面积比为4：1．

A．1 B．2 C．3 D．4
2． “车辆随机到达一个路口，遇到红灯”这个事件是( )
A．不可能事件 B．不确定事件 C．确定事件 D．必然事件
3．苹果的单价为a元/千克，香蕉的单价为b元/千克，买2千克苹果和3千克香蕉共需（　　）
A．（a+b）元 B．（3a+2b）元 C．（2a+3b）元 D．5（a+b）元
4．下列图形中一定是相似形的是( )
A．两个菱形 B．两个等边三角形 C．两个矩形 D．两个直角三角形
5．如图，在ABCD中，E为CD上一点，连接AE、BD，且AE、BD交于点F，，则DE：EC=（ ）

A．2：5 B．2：3 C．3：5 D．3：2
6．下列计算正确的是（　　）
A．x2x3＝x6 B．（m+3）2＝m2+9
C．a10÷a5＝a5 D．（xy2）3＝xy6
7．下列实数中，最小的数是（　　）
A． B． C．0 D．
8．计算3–（–9）的结果是（ ）
A．12 B．–12 C．6 D．–6
9．如图，在圆O中，直径AB平分弦CD于点E，且CD=4，连接AC，OD,若∠A与∠DOB互余，则EB的长是（ ）

A．2 B．4 C． D．2
10．如图，取一张长为、宽为的长方形纸片，将它对折两次后得到一张小长方形纸片，若要使小长方形与原长方形相似，则原长方形纸片的边应满足的条件是（ ）

A． B． C． D．
二、填空题（共7小题，每小题3分，满分21分）
11．一个多边形的每个内角都等于150°，则这个多边形是_____边形．
12．已知袋中有若干个小球，它们除颜色外其它都相同，其中只有2个红球，若随机从中摸出一个，摸到红球的概率是，则袋中小球的总个数是_____
13．如图，在两个同心圆中，四条直径把大圆分成八等份，若往圆面投掷飞镖，则飞镖落在黑色区域的概率是_______.

14．化简：= .
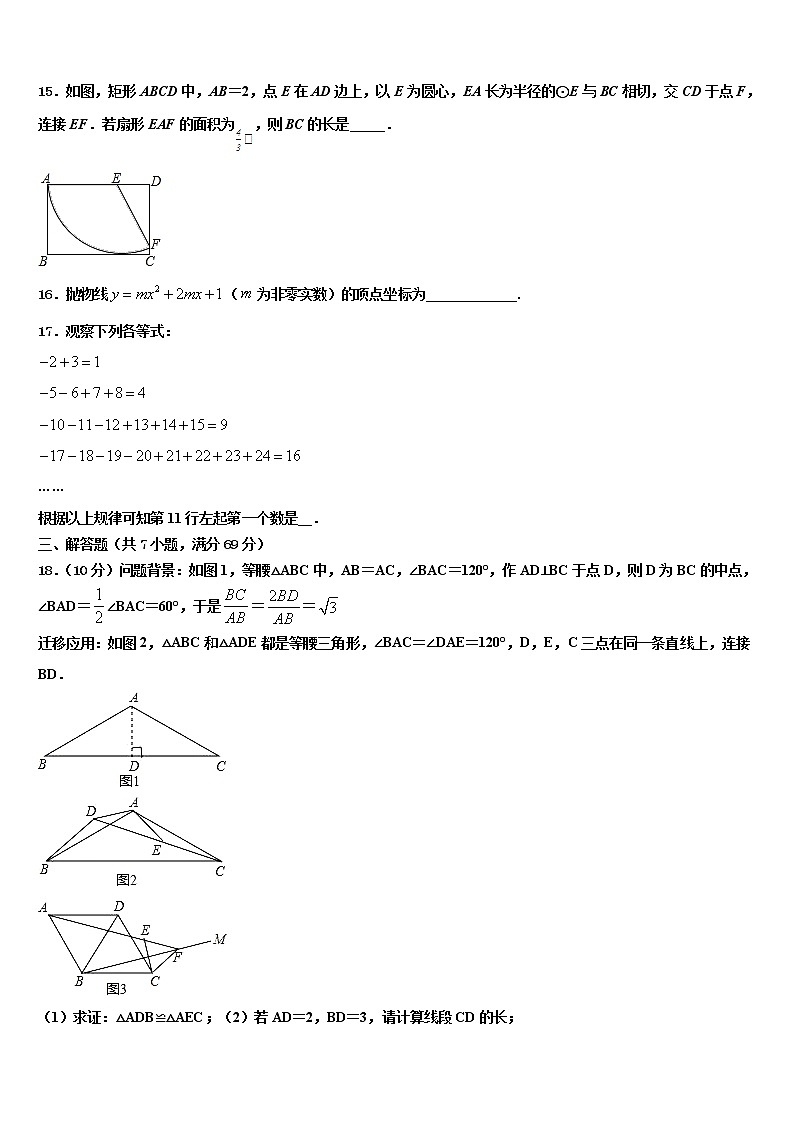
15．如图，矩形ABCD中，AB＝2，点E在AD边上，以E为圆心，EA长为半径的⊙E与BC相切，交CD于点F，连接EF．若扇形EAF的面积为，则BC的长是_____．

16．抛物线（为非零实数）的顶点坐标为_____________.
17．观察下列各等式：




……
根据以上规律可知第11行左起第一个数是__．
三、解答题（共7小题，满分69分）
18．（10分）问题背景：如图1，等腰△ABC中，AB＝AC，∠BAC＝120°，作AD⊥BC于点D，则D为BC的中点，∠BAD＝∠BAC＝60°，于是＝＝
迁移应用：如图2，△ABC和△ADE都是等腰三角形，∠BAC＝∠DAE＝120°，D，E，C三点在同一条直线上，连接BD．

（1）求证：△ADB≌△AEC；（2）若AD＝2，BD＝3，请计算线段CD的长；
拓展延伸：如图3，在菱形ABCD中，∠ABC＝120°，在∠ABC内作射线BM，作点C关于BM的对称点E，连接AE并延长交BM于点F，连接CE，CF．
（3）证明：△CEF是等边三角形；（4）若AE＝4，CE＝1，求BF的长．
19．（5分）如图，已知抛物线y＝ax2+bx+5经过A(﹣5，0)，B(﹣4，﹣3)两点，与x轴的另一个交点为C，顶点为D，连结CD．求该抛物线的表达式；点P为该抛物线上一动点(与点B、C不重合)，设点P的横坐标为t．
①当点P在直线BC的下方运动时，求△PBC的面积的最大值；
②该抛物线上是否存在点P，使得∠PBC＝∠BCD？若存在，求出所有点P的坐标；若不存在，请说明理由．

20．（8分） (1)计算：3tan30°+|2﹣|+（）﹣1﹣（3﹣π）0﹣（﹣1）2018.
(2)先化简，再求值：（x﹣）÷，其中x=，y=﹣1.
21．（10分）如图，在△OAB中，OA=OB，C为AB中点，以O为圆心，OC长为半径作圆，AO与⊙O交于点E，OB与⊙O交于点F和D，连接EF，CF，CF与OA交于点G
（1）求证：直线AB是⊙O的切线；
（2）求证：△GOC∽△GEF；
（3）若AB=4BD，求sinA的值．

22．（10分）解不等式 ，并把它的解集表示在数轴上.

23．（12分）已知四边形ABCD为正方形，E是BC的中点，连接AE，过点A作∠AFD，使∠AFD=2∠EAB，AF交CD于点F，如图①，易证：AF=CD+CF．
（1）如图②，当四边形ABCD为矩形时，其他条件不变，线段AF，CD，CF之间有怎样的数量关系？请写出你的猜想，并给予证明；
（2）如图③，当四边形ABCD为平行四边形时，其他条件不变，线段AF，CD，CF之间又有怎样的数量关系？请直接写出你的猜想．

图① 图② 图③
24．（14分）如图，△ABC内接与⊙O，AB是直径，⊙O的切线PC交BA的延长线于点P，OF∥BC交AC于AC点E，交PC于点F，连接AF

（1）判断AF与⊙O的位置关系并说明理由；
（2）若⊙O的半径为4，AF=3，求AC的长．



参考答案

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1、C
【解析】
根据位似图形的性质，得出①△ABC与△DEF是位似图形进而根据位似图形一定是相似图形得出 ②△ABC与△DEF是相似图形，再根据周长比等于位似比，以及根据面积比等于相似比的平方，即可得出答案．
【详解】
解：根据位似性质得出①△ABC与△DEF是位似图形，
②△ABC与△DEF是相似图形，
∵将△ABC的三边缩小的原来的，
∴△ABC与△DEF的周长比为2：1，
故③选项错误，
根据面积比等于相似比的平方，
∴④△ABC与△DEF的面积比为4：1．
故选C．
【点睛】
此题主要考查了位似图形的性质，中等难度,熟悉位似图形的性质是解决问题的关键．
2、B
【解析】
根据事件发生的可能性大小判断相应事件的类型即可.
【详解】
“车辆随机到达一个路口，遇到红灯”是随机事件.
故选：.
【点睛】
本题考查了随机事件，解决本题需要正确理解必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下，一定发生的实际；不可能事件是指在一定条件下，一定不发生的事件；不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件.
3、C
【解析】
用单价乘数量得出买2千克苹果和3千克香蕉的总价，再进一步相加即可．
【详解】
买单价为a元的苹果2千克用去2a元，买单价为b元的香蕉3千克用去3b元，
共用去：(2a+3b)元.
故选C.
【点睛】
本题主要考查列代数式，总价=单价乘数量.
4、B
【解析】
如果两个多边形的对应角相等，对应边的比相等，则这两个多边形是相似多边形．
【详解】
解：∵等边三角形的对应角相等，对应边的比相等，
∴两个等边三角形一定是相似形，
又∵直角三角形，菱形的对应角不一定相等，矩形的边不一定对应成比例，
∴两个直角三角形、两个菱形、两个矩形都不一定是相似形，
故选：B．
【点睛】
本题考查了相似多边形的识别．判定两个图形相似的依据是：对应边成比例，对应角相等，两个条件必须同时具备．
5、B
【解析】
∵四边形ABCD是平行四边形，
∴AB∥CD
∴∠EAB=∠DEF，∠AFB=∠DFE
∴△DEF∽△BAF
∴
∵，
∴DE：AB=2：5
∵AB=CD，
∴DE：EC=2：3
故选B
6、C
【解析】
根据乘方的运算法则、完全平方公式、同底数幂的除法和积的乘方进行计算即可得到答案.
【详解】
x2•x3＝x5，故选项A不合题意；
（m+3）2＝m2+6m+9，故选项B不合题意；
a10÷a5＝a5，故选项C符合题意；
（xy2）3＝x3y6，故选项D不合题意．
故选：C．
【点睛】
本题考查乘方的运算法则、完全平方公式、同底数幂的除法和积的乘方解题的关键是掌握乘方的运算法则、完全平方公式、同底数幂的除法和积的乘方的运算.
7、B
【解析】
根据正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小，进行比较．
【详解】
∵<-2<0<，
∴最小的数是-π，
故选B．
【点睛】
此题主要考查了比较实数的大小，要熟练掌握任意两个实数比较大小的方法．（1）正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小．（2）利用数轴也可以比较任意两个实数的大小，即在数轴上表示的两个实数，右边的总比左边的大，在原点左侧，绝对值大的反而小．
8、A
【解析】
根据有理数的减法，即可解答．
【详解】

故选A．
【点睛】
本题考查了有理数的减法，解决本题的关键是熟记减去一个数等于加上这个数的相
反数．
9、D
【解析】
连接CO，由直径AB平分弦CD及垂径定理知∠COB=∠DOB，则∠A与∠COB互余，由圆周角定理知∠A=30°，∠COE=60°，则∠OCE=30°，设OE=x,则CO=2x,利用勾股定理即可求出x，再求出BE即可.
【详解】
连接CO，∵AB平分CD，
∴∠COB=∠DOB，AB⊥CD，CE=DE=2
∵∠A与∠DOB互余，
∴∠A+∠COB=90°，
又∠COB=2∠A，
∴∠A=30°，∠COE=60°，
∴∠OCE=30°，
设OE=x,则CO=2x,
∴CO2=OE2+CE2
即(2x)2=x2+(2)2
解得x=2，
∴BO=CO=4，
∴BE=CO-OE=2.
故选D.

【点睛】
此题主要考查圆内的综合问题，解题的关键是熟知垂径定理、圆周角定理及勾股定理.
10、B
【解析】
由题图可知：得对折两次后得到的小长方形纸片的长为，宽为，然后根据相似多边形的定义，列出比例式即可求出结论．
【详解】
解：由题图可知：得对折两次后得到的小长方形纸片的长为，宽为，
∵小长方形与原长方形相似，


故选B．
【点睛】
此题考查的是相似三角形的性质，根据相似三角形的定义列比例式是解决此题的关键．

二、填空题（共7小题，每小题3分，满分21分）
11、1
【解析】
根据多边形的内角和定理：180°•（n-2）求解即可．
【详解】
由题意可得：180°•（n-2）=150°•n，
解得n=1．
故多边形是1边形．
12、8个
【解析】
根据概率公式结合取出红球的概率即可求出袋中小球的总个数．
【详解】
袋中小球的总个数是：2÷=8（个）．
故答案为8个．
【点睛】
本题考查了概率公式，根据概率公式算出球的总个数是解题的关键．
13、
【解析】
试题解析：∵两个同心圆被等分成八等份，飞镖落在每一个区域的机会是均等的，其中白色区域的面积占了其中的四等份，
∴P（飞镖落在白色区域）=.
14、２
【解析】
根据算术平方根的定义，求数a的算术平方根，也就是求一个正数x，使得x2=a，则x就是a的算术平方根， 特别地，规定0的算术平方根是0.
【详解】
∵22=4，∴=2.
【点睛】
本题考查求算术平方根，熟记定义是关键.
15、1
【解析】
分析：设∠AEF=n°，由题意，解得n=120，推出∠AEF=120°，在Rt△EFD中，求出DE即可解决问题．
详解：设∠AEF=n°，
由题意，解得n=120，
∴∠AEF=120°，
∴∠FED=60°，
∵四边形ABCD是矩形，
∴BC=AD，∠D=90°，
∴∠EFD=10°，
∴DE=EF=1，
∴BC=AD=2+1=1，
故答案为1．

点睛：本题考查切线的性质、矩形的性质、扇形的面积公式、直角三角形10度角性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
16、
【解析】
【分析】将抛物线的解析式由一般式化为顶点式，即可得到顶点坐标.
【详解】y=mx2+2mx+1
=m(x2+2x)+1
=m(x2+2x+1-1)+1
=m(x+1)2 +1-m，
所以抛物线的顶点坐标为（-1，1-m），
故答案为（-1，1-m）.
【点睛】本题考查了抛物线的顶点坐标，把抛物线的解析式转化为顶点式是解题的关键.
17、-1．
【解析】
观察规律即可解题.
【详解】
解：第一行=12=1,第二行=22=4,第三行=32=9...
∴第n行=n2,第11行=112=121,
又∵左起第一个数比右侧的数大一,
∴第11行左起第一个数是-1.
【点睛】
本题是一道规律题,属于简单题，认真审题找到规律是解题关键.

三、解答题（共7小题，满分69分）
18、（1）见解析；（2）CD =；（3）见解析；（4）
【解析】
试题分析：迁移应用：（1）如图2中，只要证明∠DAB=∠CAE，即可根据SAS解决问题；
（2）结论：CD=AD+BD．由△DAB≌△EAC，可知BD=CE，在Rt△ADH中，DH=AD•cos30°= AD，由AD=AE，AH⊥DE，推出DH=HE，由CD=DE+EC=2DH+BD=AD+BD，即可解决问题；
拓展延伸：（3）如图3中，作BH⊥AE于H，连接BE．由BC=BE=BD=BA，FE=FC，推出A、D、E、C四点共圆，推出∠ADC=∠AEC=120°，推出∠FEC=60°，推出△EFC是等边三角形；
（4）由AE=4，EC=EF=1，推出AH=HE=2，FH=3，在Rt△BHF中，由∠BFH=30°，可得=cos30°，由此即可解决问题．
试题解析：
迁移应用：（1）证明：如图2，

∵∠BAC=∠DAE=120°，
∴∠DAB=∠CAE，
在△DAE和△EAC中，
DA=EA，∠DAB=∠EAC，AB=AC，
∴△DAB≌△EAC，
（2）结论：CD=AD+BD．
理由：如图2-1中，作AH⊥CD于H．

∵△DAB≌△EAC，
∴BD=CE，
在Rt△ADH中，DH=AD•cos30°=AD，
∵AD=AE，AH⊥DE，
∴DH=HE，
∵CD=DE+EC=2DH+BD=AD+BD=．
拓展延伸：（3）如图3中，作BH⊥AE于H，连接BE．

∵四边形ABCD是菱形，∠ABC=120°，
∴△ABD，△BDC是等边三角形，
∴BA=BD=BC，
∵E、C关于BM对称，
∴BC=BE=BD=BA，FE=FC，
∴A、D、E、C四点共圆，
∴∠ADC=∠AEC=120°，
∴∠FEC=60°，
∴△EFC是等边三角形，
（4）∵AE=4，EC=EF=1，
∴AH=HE=2，FH=3，
在Rt△BHF中，∵∠BFH=30°，
∴ =cos30°，
∴BF=．
19、 (1)y＝x2+6x+5；(2)①S△PBC的最大值为；②存在，点P的坐标为P(﹣，﹣)或(0，5)．
【解析】
(1)将点A、B坐标代入二次函数表达式，即可求出二次函数解析式；
(2)①如图1，过点P作y轴的平行线交BC于点G，将点B、C的坐标代入一次函数表达式并解得：直线BC的表达式为：y＝x+1，设点G(t，t+1)，则点P(t，t2+6t+5)，利用三角形面积公式求出最大值即可；
②设直线BP与CD交于点H，当点P在直线BC下方时，求出线段BC的中点坐标为(﹣，﹣)，过该点与BC垂直的直线的k值为﹣1，求出 直线BC中垂线的表达式为：y＝﹣x﹣4…③，同理直线CD的表达式为：y＝2x+2…④，、联立③④并解得：x＝﹣2，即点H(﹣2，﹣2)，同理可得直线BH的表达式为：y＝x﹣1…⑤，联立⑤和y＝x2+6x+5并解得：x＝﹣，即可求出P点；当点P(P′)在直线BC上方时，根据∠PBC＝∠BCD求出BP′∥CD，求出直线BP′的表达式为：y＝2x+5，联立y＝x2+6x+5和y＝2x+5，求出x，即可求出P.
【详解】
解：(1)将点A、B坐标代入二次函数表达式得：，
解得：，
故抛物线的表达式为：y＝x2+6x+5…①，
令y＝0，则x＝﹣1或﹣5，
即点C(﹣1，0)；
(2)①如图1，过点P作y轴的平行线交BC于点G，

将点B、C的坐标代入一次函数表达式并解得：
直线BC的表达式为：y＝x+1…②，
设点G(t，t+1)，则点P(t，t2+6t+5)，
S△PBC＝PG(xC﹣xB)＝(t+1﹣t2﹣6t﹣5)＝﹣t2﹣t﹣6，
∵-＜0，
∴S△PBC有最大值，当t＝﹣时，其最大值为；
②设直线BP与CD交于点H，

当点P在直线BC下方时，
∵∠PBC＝∠BCD，
∴点H在BC的中垂线上，
线段BC的中点坐标为(﹣，﹣)，
过该点与BC垂直的直线的k值为﹣1，
设BC中垂线的表达式为：y＝﹣x+m，将点(﹣，﹣)代入上式并解得：
直线BC中垂线的表达式为：y＝﹣x﹣4…③，
同理直线CD的表达式为：y＝2x+2…④，
联立③④并解得：x＝﹣2，即点H(﹣2，﹣2)，
同理可得直线BH的表达式为：y＝x﹣1…⑤，
联立①⑤并解得：x＝﹣或﹣4(舍去﹣4)，
故点P(﹣，﹣)；
当点P(P′)在直线BC上方时，
∵∠PBC＝∠BCD，∴BP′∥CD，
则直线BP′的表达式为：y＝2x+s，将点B坐标代入上式并解得：s＝5，
即直线BP′的表达式为：y＝2x+5…⑥，
联立①⑥并解得：x＝0或﹣4(舍去﹣4)，
故点P(0，5)；
故点P的坐标为P(﹣，﹣)或(0，5)．
【点睛】
本题考查的是二次函数，熟练掌握抛物线的性质是解题的关键.
20、 (1)3；(2) x﹣y，1．
【解析】
（1）根据特殊角的三角函数值、绝对值、负整数指数幂、零指数幂可以解答本题；
（2）根据分式的减法和除法可以化简题目中的式子，然后将x、y的值代入化简后的式子即可解答本题．
【详解】
（1）3tan30°+|2-|+（）-1-（3-π）0-（-1）2018
=3×+2-+3-1-1，
=+2−+3-1-1，
=3；
（2）（x﹣）÷，
=，
=
=x-y，
当x=，y=-1时，原式=−+1=1．
【点睛】
本题考查特殊角的三角函数值、绝对值、负整数指数幂、零指数幂、分式的化简求值，解答本题的关键是明确它们各自的计算方法．
21、 (1)见解析;(2)见解析;(3).
【解析】
（1）利用等腰三角形的性质，证明OC⊥AB即可；
（2）证明OC∥EG，推出△GOC∽△GEF即可解决问题；
（3）根据勾股定理和三角函数解答即可．
【详解】
证明：（1）∵OA=OB，AC=BC，
∴OC⊥AB，
∴⊙O是AB的切线．
（2）∵OA=OB，AC=BC，
∴∠AOC=∠BOC，
∵OE=OF，
∴∠OFE=∠OEF，
∵∠AOB=∠OFE+∠OEF，
∴∠AOC=∠OEF，
∴OC∥EF，
∴△GOC∽△GEF，
∴，
∵OD=OC，
∴OD•EG=OG•EF．
（3）∵AB=4BD，
∴BC=2BD，设BD=m，BC=2m，OC=OD=r，
在Rt△BOC中，∵OB2=OC2+BC2，
即（r+m）2=r2+（2m）2，
解得：r=1.5m，OB=2.5m，
∴sinA=sinB=.
【点睛】
考查圆的综合题，考查切线的判定、等腰三角形的性质、平行线的性质、勾股定理等知识，解题的关键是灵活运用所学知识解决问题．
22、x＜5；数轴见解析
【解析】
【分析】将（x-2）当做一个整体，先移项，然后再按解一元一次不等式的一般步骤进行求解，求得解集后在数轴上表示即可.
【详解】移项，得 ，
去分母，得 ，
移项，得，
∴不等式的解集为，
在数轴上表示如图所示：

【点睛】本题考查了解一元一次不等式，在数轴上表示不等式的解集，根据不等式的特点选择恰当的方法进行求解是关键.
23、（1）图②结论：AF=CD+CF. （2）图③结论：AF=CD+CF.
【解析】
试题分析：（1）作，的延长线交于点.证三角形全等，进而通过全等三角形的对应边相等验证之间的关系；
（2）延长交的延长线于点由全等三角形的对应边相等验证关系.
试题解析：（1）图②结论：
证明：作，的延长线交于点.

∵四边形是矩形，




由是中点，可证≌


（2）图③结论：
延长交的延长线于点如图所示

因为四边形是平行四边形
所以//且,
因为为的中点，所以也是的中点，
所以
又因为

所以
又因为
所以≌
所以
因为

24、解：（1）AF与圆O的相切．理由为：
如图，连接OC，

∵PC为圆O切线，∴CP⊥OC．
∴∠OCP=90°．
∵OF∥BC，
∴∠AOF=∠B，∠COF=∠OCB．
∵OC=OB，∴∠OCB=∠B．∴∠AOF=∠COF．
∵在△AOF和△COF中，OA=OC，∠AOF=∠COF，OF=OF，
∴△AOF≌△COF（SAS）．∴∠OAF=∠OCF=90°．
∴AF为圆O的切线，即AF与⊙O的位置关系是相切．
（2）∵△AOF≌△COF，∴∠AOF=∠COF．
∵OA=OC，∴E为AC中点，即AE=CE=AC，OE⊥AC．
∵OA⊥AF，∴在Rt△AOF中，OA=4，AF=3，根据勾股定理得：OF=1．
∵S△AOF=•OA•AF=•OF•AE，∴AE=．
∴AC=2AE=．
【解析】
试题分析：（1）连接OC，先证出∠3=∠2，由SAS证明△OAF≌△OCF，得对应角相等∠OAF=∠OCF，再根据切线的性质得出∠OCF=90°，证出∠OAF=90°，即可得出结论；
（2）先由勾股定理求出OF，再由三角形的面积求出AE，根据垂径定理得出AC=2AE．
试题解析：（1）连接OC，如图所示：

∵AB是⊙O直径，
∴∠BCA=90°，
∵OF∥BC，
∴∠AEO=90°，∠1=∠2，∠B=∠3，
∴OF⊥AC，
∵OC=OA，
∴∠B=∠1，
∴∠3=∠2，
在△OAF和△OCF中，
，
∴△OAF≌△OCF（SAS），
∴∠OAF=∠OCF，
∵PC是⊙O的切线，
∴∠OCF=90°，
∴∠OAF=90°，
∴FA⊥OA，
∴AF是⊙O的切线；
（2）∵⊙O的半径为4，AF=3，∠OAF=90°，
∴OF==1
∵FA⊥OA，OF⊥AC，
∴AC=2AE，△OAF的面积=AF•OA=OF•AE，
∴3×4=1×AE，
解得：AE=，
∴AC=2AE=．
考点：1.切线的判定与性质；2.勾股定理；3.相似三角形的判定与性质．