2022版高考数学二轮复习 第2篇 专题2 数列 第2讲 数列求和及数列的简单应用课件

这是一份2022版高考数学二轮复习 第2篇 专题2 数列 第2讲 数列求和及数列的简单应用课件，共60页。PPT课件主要包含了专题二数列，高频考点，真题热身，感悟高考，典例1，an＝n2＋1，典例2，典例3，n·2n，典例4等内容，欢迎下载使用。
第二讲　数列求和及数列的简单应用
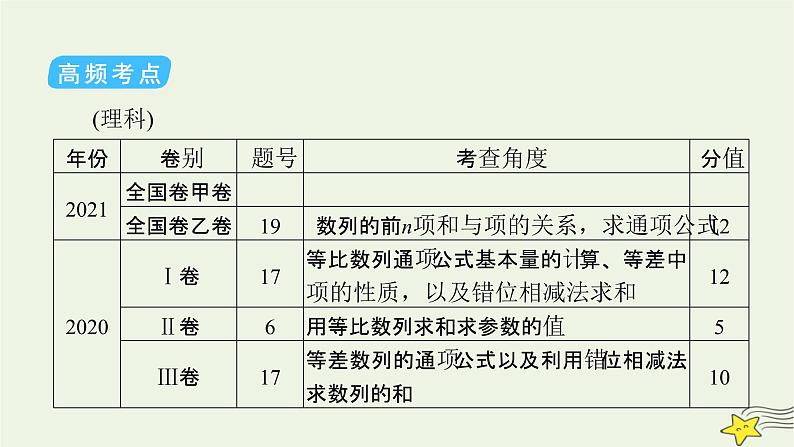
导航立前沿•考点启方向
自主先热身•真题定乾坤
核心拔头筹•考点巧突破
明晰易错点•高考零失误
1．高考对数列求和的考查主要以解答题的形式出现，通过分组转化、错位相减、裂项相消等方法求数列的前n项和，难度中等偏下．2．在考查数列求和的同时，将数列与函数、不等式交汇渗透．
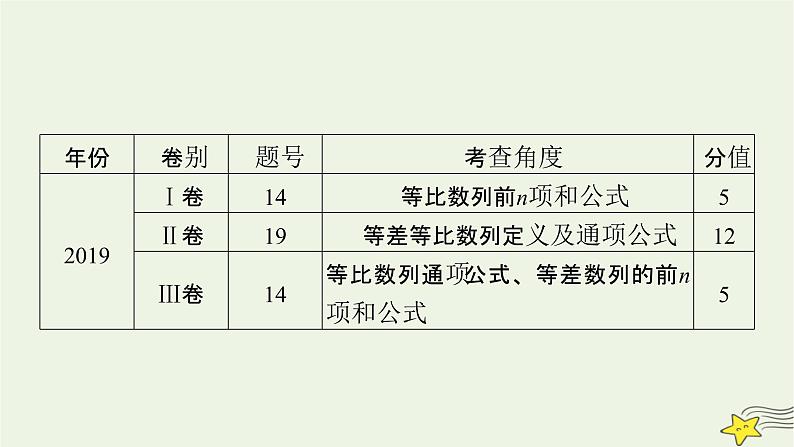
(理科)1．(2020·全国卷Ⅱ卷)数列{an}中，a1＝2，am＋n＝aman，若ak＋1＋ak＋2＋…＋ak＋10＝215-25，则k＝(　　)A．2B．3　C．4　D．5
2．(2020·全国卷Ⅰ卷)数列{an}满足an＋2＋(-1)nan＝3n-1，前16项和为540，则a1＝______.
【解析】　an＋2＋(-1)nan＝3n-1，当n为奇数时，an＋2＝an＋3n-1；当n为偶数时，an＋2＋an＝3n-1.设数列{an}的前n项和为Sn，S16＝a1＋a2＋a3＋a4＋…＋a16＝a1＋a3＋a5…＋a15＋(a2＋a4)＋…(a14＋a16)＝a1＋(a1＋2)＋(a1＋10)＋(a1＋24)＋(a1＋44)＋(a1＋70)＋(a1＋102)＋(a1＋140)＋(5＋17＋29＋41)＝8a1＋392＋92＝8a1＋484＝540，∴a1＝7故答案为7.
4．(2020·全国卷Ⅰ卷)设{an}是公比不为1的等比数列，a1为a2，a3的等差中项．(1)求{an}的公比；(2)若a1＝1，求数列{nan}的前n项和．【解析】　(1)设{an}的公比为q，a1为a2，a3的等差中项，∵2a1＝a2＋a3，a1≠0，∴q2＋q-2＝0，∵q≠1，∴q＝-2.
5．(2020·全国卷Ⅲ卷)设数列{an}满足a1＝3，an＋1＝3an-4n.(1)计算a2，a3，猜想{an}的通项公式并加以证明；(2)求数列{2nan}的前n项和Sn.
【解析】　(1)由题意可得a2＝3a1-4＝9-4＝5，a3＝3a2-8＝15-8＝7，由数列{an}的前三项可猜想数列{an}是以3为首项，2为公差的等差数列，即an＝2n＋1，证明如下：当n＝1时，a1＝3成立；假设n＝k时，ak＝2k＋1成立．那么n＝k＋1时，ak＋1＝3ak-4k＝3(2k＋1)-4k＝2k＋3＝2(k＋1)＋1也成立．则对任意的n∈N*，都有an＝2n＋1成立．
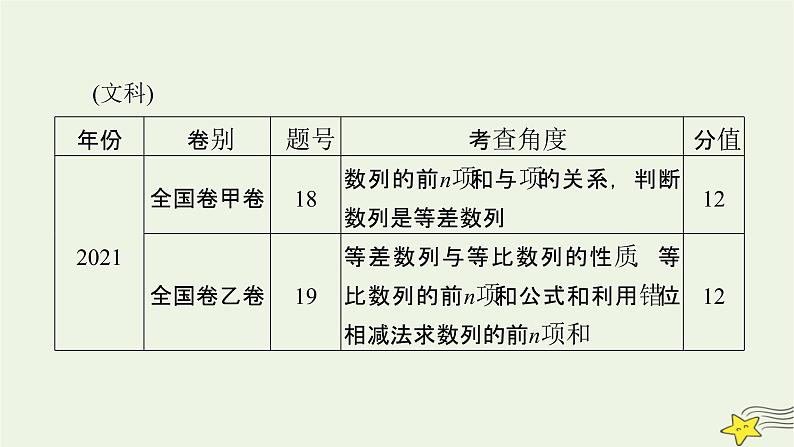
(文科)1．(2020·全国卷Ⅱ卷)数列{an}中，a1＝2，am＋n＝aman，若ak＋1＋ak＋2＋…＋ak＋10＝215-25，则k＝(　　)A．2B．3　C．4　D．5
2．(2020·全国卷Ⅰ卷)数列{an}满足an＋2＋(-1)nan＝3n-1，前16项和为540，则a1＝______.【解析】　an＋2＋(-1)nan＝3n-1，当n为奇数时，an＋2＝an＋3n-1；当n为偶数时，an＋2＋an＝3n-1.设数列{an}的前n项和为Sn，S16＝a1＋a2＋a3＋a4＋…＋a16＝a1＋a3＋a5…＋a15＋(a2＋a4)＋…(a14＋a16)＝a1＋(a1＋2)＋(a1＋10)＋(a1＋24)＋(a1＋44)＋(a1＋70)＋(a1＋102)＋(a1＋140)＋(5＋17＋29＋41)＝8a1＋392＋92＝8a1＋484＝540，∴a1＝7故答案为7.
3．(2020·全国卷Ⅱ卷)记Sn为等差数列{an}的前n项和．若a1＝-2，a2＋a6＝2，则S10＝________.【解析】　∵{an}是等差数列，且a1＝-2，a2＋a6＝2，设{an}等差数列的公差d，根据等差数列通项公式：an＝a1＋(n-1)d，可得a1＋d＋a1＋5d＝2，即：-2＋d＋(-2)＋5d＝2，整理可得：6d＝6，解得：d＝1.
1．高考主要考查两种基本数列(等差数列、等比数列)、两种数列求和方法(裂项求和法、错位相减法)、两类综合(与函数综合、与不等式综合)，主要突出数学思想的应用．2．若以解答题形式考查，数列往往与解三角形在17题的位置上交替考查，试题难度中等；若以客观题考查，难度中等的题目较多，但有时也出现在第12题或16题位置上，难度偏大，复习时应引起关注．
考点一　求数列的通项公式
角度1　公式法求数列通项记Sn为数列{an}的前n项和．若Sn＝2an＋1，则S6＝__________.
解法二：由Sn＝2an＋1，得S1＝2S1＋1，所以S1＝-1，当n≥2时，由Sn＝2an＋1得Sn＝2(Sn-Sn-1)＋1，即Sn＝2Sn-1-1，∴Sn-1＝2(Sn-1-1)，又S1-1＝-2，∴{Sn-1}是首项为-2，公比为2的等比数列，所以Sn-1＝-2×2n-1＝-2n，所以Sn＝1-2n，∴S6＝1-26＝-63.
角度2　累加法、累乘法求数列通项(1)已知数列{an}中，a1＝2，an＋1-1＝an＋2n，则数列{an}的通项公式为______________.(2)若数列{an}满足a1＝1，an＋1＝2nan，则数列{an}的通项公式an＝____________.
角度3　构造法求数列通项已知正项数列{an}中，a1＝2，an＋1＝2an＋3×2n，则数列{an}的通项公式为__________________________.
an＝(3n-1)·2n-1　
[探究追问]　若本例中的“an＋1＝2an＋3×2n”改为“an＋1＝2an＋3×5n”，其他条件不变，则数列{an}的通项公式为____________________.
an＝5n-3×2n-1　
解法二：设an＋1＋k·5n＋1＝2(an＋k×5n)，则an＋1＝2an-3k×5n，与题中递推公式比较得k＝-1，即an＋1-5n＋1＝2(an-5n)，所以数列{an-5n}是首项为a1-5＝-3，公比为2的等比数列，则an-5n＝-3×2n-1，故an＝5n-3×2n-1.
求数列通项公式的两种策略(1)已知Sn与an的递推关系求通项常用两个思路：一是利用Sn-Sn-1＝an(n≥2)转化为an的递推关系，再求其通项公式；二是转化为Sn的递推关系，先求出Sn与n之间的关系，再求an.(2)已知an与an＋1的递推关系式求通项，通常结合关系式的特征采用累加、累乘、构造等方法．
2．已知数列{an}的前n项和为Sn，若Sn＝2an-2n，则Sn＝__________.
数列求和的方法(1)分组求和法：分组求和法是解决通项公式可以写成cn＝an＋bn形式的数列求和问题的方法，其中{an}与{bn}是等差(比)数列或一些可以直接求和的数列．
考点二　求数列的前n项和
数列求和的解题策略(1)解决数列求和问题，一般首先确定数列的通项公式，然后根据其结构形式，采取相适应的求解方法．(2)裂项系数取决于前后两项分母的差，裂项相消后，前、后保留的项数一样多．(3)用错位相减法求和时，要注意找准项数、开始的项和结束的项，不要漏项或加项．在错位相减后一定要注意其中各个项的结构，特别是相减后得到的和式的第一项是否可以和后续的项组成等比数列．
易错点一：用裂项相消法求和时漏项或添项
易错点二：错位相减法求和时项的位置处理不当致误