专题07方程与不等式（教师版含解析）-2022年初升高数学衔接讲义（第1套）

专题07方程与不等式

一元二次不等式的解法是初中阶段一元一次不等式或一元一次不等式组的延续和深化，也与后面的线性规划、直线与圆锥曲线以及导数等内容密切相关，许多问题的解决都会借助一元二次不等式的解法.一元二次不等式的解法在整个高中数学中具有很强的基础性和工具性.

一元二次不等式、一元二次函数与一元二次方程三者之间有着密切联系，理解并掌握利用二次函数的图象确定一元二次不等式解集的方法即图象法，其本质就是要能利用数形结合的思想方法认识方程的解，不等式的解集与函数图象上对应点的横坐标的内在联系.

二次函数图象是连接三个“二次”的纽带，是理解和解决问题的关键，要深入理解三者之间的区别及联系，掌握函数、方程及不等式的思想和方法.一元二次不等式的解题步骤：

①.将含x的式子用y来表示，构建一个一元二次函数；

②.令这个函数中的y=0，构建一个一元二次方程，求出对应方程的解，即找到图中的关键点——函数的零点；

③.利用图象开口与零点画出对应函数的草图；

④观察草图，得出不等式所对应的解集.

方程

是一个含有两个未知数,并且含有未知数的项的最高次数是2的整式方程,这样的方程叫做二元二次方程．其中,,叫做这个方程的二次项,,叫做一次项,6叫做常数项．

我们看下面的两个方程组：

第一个方程组是由一个二元二次方程和一个二元一次方程组成的，第二个方程组是由两个二元二次方程组成的，像这样的方程组叫做二元二次方程组．

下面我们主要来研究由一个二元二次方程和一个二元一次方程组成的方程组的解法．

一个二元二次方程和一个二元一次方程组成的方程组一般可以用代入消元法来解．

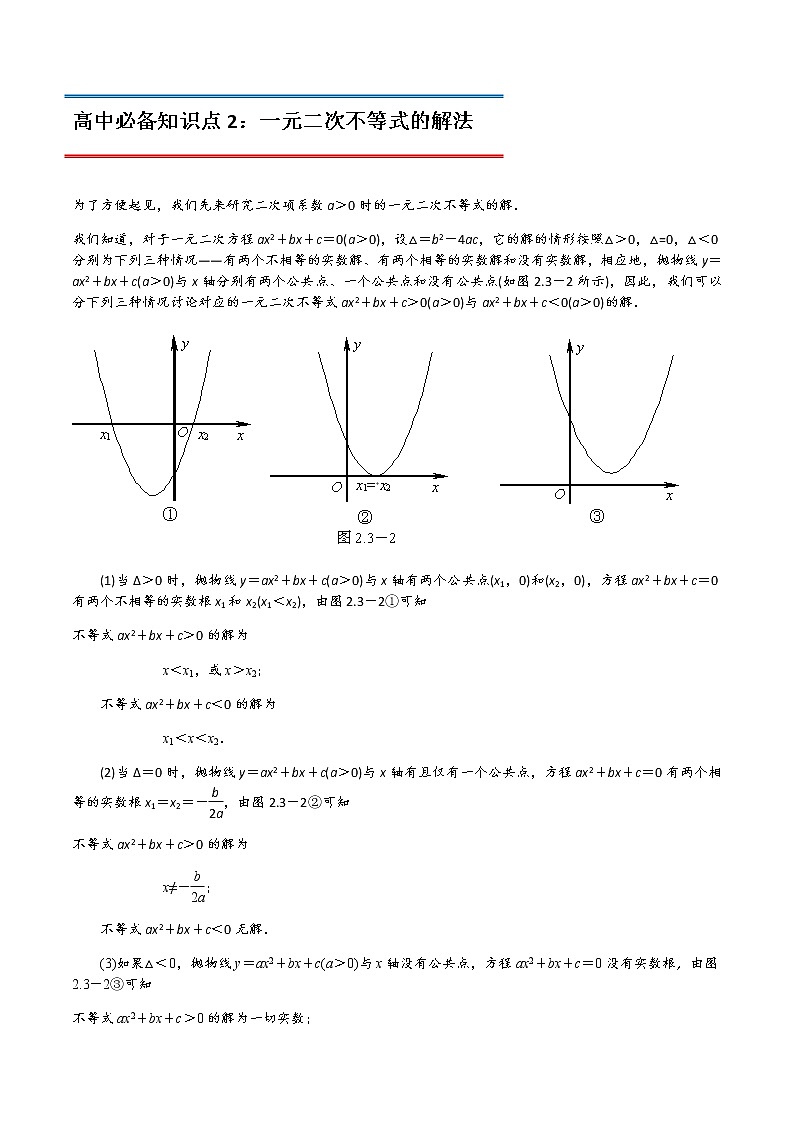
为了方便起见，我们先来研究二次项系数a＞0时的一元二次不等式的解．

我们知道，对于一元二次方程ax2＋bx＋c＝0(a＞0)，设△＝b2－4ac，它的解的情形按照△＞0，△=0，△＜0分别为下列三种情况——有两个不相等的实数解、有两个相等的实数解和没有实数解，相应地，抛物线y＝ax2＋bx＋c(a＞0)与x轴分别有两个公共点、一个公共点和没有公共点(如图2.3－2所示)，因此，我们可以分下列三种情况讨论对应的一元二次不等式ax2＋bx＋c＞0(a＞0)与ax2＋bx＋c＜0(a＞0)的解．

 (1)当Δ＞0时，抛物线y＝ax2＋bx＋c(a＞0)与x轴有两个公共点(x1，0)和(x2，0)，方程ax2＋bx＋c＝0有两个不相等的实数根x1和x2(x1＜x2)，由图2.3－2①可知

不等式ax2＋bx＋c＞0的解为

             x＜x1，或x＞x2；

    不等式ax2＋bx＋c＜0的解为

             x1＜x＜x2．

    (2)当Δ＝0时，抛物线y＝ax2＋bx＋c(a＞0)与x轴有且仅有一个公共点，方程ax2＋bx＋c＝0有两个相等的实数根x1＝x2＝－，由图2.3－2②可知

不等式ax2＋bx＋c＞0的解为

             x≠－；

    不等式ax2＋bx＋c＜0无解．

 (3)如果△＜0，抛物线y＝ax2＋bx＋c(a＞0)与x轴没有公共点，方程ax2＋bx＋c＝0没有实数根，由图2.3－2③可知

不等式ax2＋bx＋c＞0的解为一切实数；

不等式ax2＋bx＋c＜0无解．

 今后，我们在解一元二次不等式时，如果二次项系数大于零，可以利用上面的结论直接求解；如果二次项系数小于零，则可以先在不等式两边同乘以－1，将不等式变成二次项系数大于零的形式，再利用上面的结论去解不等式．

【典型例题】

已知方程组有两组相等的实数解，求的值，并求出此时方程组的解.

【变式训练】

解方程组：

【能力提升】

解方程组：

【典型例题】

解下列不等式：

(1)－3x2－2x＋8≥0；

(2)0＜x2－x－2≤4；

【变式训练】

求不等式的解．

【能力提升】

解下列不等式：

(1)；

(2)；

(3)．

1．若实数a使关于x的不等式组至少有3个整数解，且使关于y的分式方程有正整数解，则符合条件的所有整数a的和为(    )

A． B． C． D．

2．不等式组的解集为(    )

A． B． C． D．无解

3．已知关于的分式方程有整数解，且关于的不等式组有且只有3个负整数解，则符合条件的所有整数的个数为(      )

A．1 B．2 C．3 D．4

4．已知不等式组的解为：，则的值为(    )

A．1 B．2020 C．-1 D．-2020

5．下面是解不等式的过程，每一步只对上一步负责，则其中有错的步骤是(    )

A．只有④ B．①③ C．②④ D．①②④

6．下列命题正确的是(    )

A．若，则 B．m，n为整数，若，则

C．若，则 D．若，则

7．不等式组的解集在数轴上表示为( )

A． B．

C． D．

8．若关于的一元一次不等式组恰有3个整数解，且一次函数不经过第三象限，则所有满足条件的整数的值之和是(　　　)

A． B． C．0 D．1

9．关于的不等式组只有3个整数解，求的取值范围(    )

A． B． C． D．

10．若整数a是使得关于x的不等式组有且只有2个整数解，且使得且关于y的分式方程＋＝a有非负数解，则所有满足条件的整数a的个数为(    )

A．6 B．5 C．4 D．3

11．不等式组的解集是______．

12．已知二次函数的图象与轴有且只有一个公共点，则一元二次不等式的解集为________．

13．已知二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，则一元二次不等式ax2＋bx＋c＞0的解是______．

14．已知二次函数的部分图象如图所示，则关于的一元二次不等式的解集为______________________．

15．已知二次函数的顶点坐标及部分图象(如图所示)，其中图象与横轴的正半轴交点为，由图象可知：

①当________时，函数值随着的增大而减小；

②关于的一元二次不等式的解是________．

16．自主学习，请阅读下列解题过程．

解一元二次不等式：＞0．

解：设=0，解得：=0，=5，则抛物线y=与x轴的交点坐标为(0，0)和(5，0)．画出二次函数y=的大致图象(如图所示)，由图象可知：当x＜0，或x＞5时函数图象位于x轴上方，此时y＞0，即＞0，所以，一元二次不等式＞0的解集为：x＜0或x＞5．

通过对上述解题过程的学习，按其解题的思路和方法解答下列问题：

(1)上述解题过程中，渗透了下列数学思想中的     和     ．(只填序号)

①转化思想     ②分类讨论思想    ③数形结合思想

(2)一元二次不等式＜0的解集为             ．

(3)用类似的方法解一元二次不等式：＞0．

17．不等式组的解集为，则的取值范围为_____．

18．不等式组的整数解的个数是_________．

19．关于的不等式组恰好只有三个整数解，则的取值范围是_____________.

20．对于满足0≤p≤4的一切实数，不等式x2+px＞4x+p﹣3恒成立，则实数x的取值范围是_______．

21．请阅读下列解题过程：

解一元二次不等式：x2－3x＞0．

解：x(x－3)＞0，

∴或，

解得x＞3或x＜0．

∴一元二次不等式x2－3x＞0的解集为x＜0或x＞3．

结合上述解题过程回答下列问题：

(1)上述解题过程渗透的数学思想为　　　　；

(2)一元二次不等式x2－3x＜0的解集为　　　　；

(3)请用类似的方法解一元二次不等式：x2－2x－3＜0．

22．先阅读理解下列题，再按要求完成问题：

例题：解一元二次不等式

 解：把分解因式得：

又所以由有理数乘法法则“两数相乘，同号得正”，有

(1)或(2)，解不等式组(1)，得

解不等式(2)，得因此，一元二次不等式的解集为或；

问题；根据阅读解不等式：.

23．请阅读下列解题过程：

解一元二次不等式：.

解：

，或，

解得或.

一元二次不等式的解集为或.

结合上述解答过程回答下列问题：

(1)上述解题过程渗透的数学思想为________；

(2)一元二次不等式的解集为________；

(3)请用类似的方法解一元二次不等式：.

24．阅读材料，解答问题.

例：用图象法解一元二次不等式：

解：设，则是的二次函数.∵，

∴抛物线开口向上.

又∵当时，，解得，.

∴由此得抛物线的大致图象如图所示.

观察函数图象可知：当或时，.

∴的解集是：或.

(1)观察图象，直接写出一元二次不等式：的解集是______；

(2)仿照材料、用图象法解一元二次不等式：.

25．阅读材料，解答问题：

例：用图象法解一元二次不等式：．

解：设，则是的二次函数．

抛物线开口向上．

又当时，，解得．

由此得抛物线的大致图象如图所示．

观察函数图象可知：当或时，．的解集是：或．

(1)观察图象，直接写出一元二次不等式：的解集是      ；

(2)仿照上例，用图象法解一元二次不等式：．

26．先阅读理解下面的例题，再按要求解答后面的问题

例题：解一元二次不等式＞0.解：令y=，画出y=如图所示，

由图像可知：当x＜1或x＞2时，y＞0.所以一元二次不等式＞0的解集为x＜1或x＞2.

填空：(1)＜0的解集为                              ；

(2)＞0的解集为                              ；

用类似的方法解一元二次不等式＞0.

27．解一元二次不等式 ．

请按照下面的步骤，完成本题的解答．

解： 可化为 ．   

(1)依据“两数相乘，同号得正”，可得不等式组①  或不等式组②________．   

(2)解不等式组①，得________．   

(3)解不等式组②，得________．   

(4)一元二次不等式 的解集为________．

28．先阅读下面的例题，再按要求解答后面的问题．

例题：解一元二次不等式x2﹣3x+2＞0

解：令y=x2﹣3x+2，画出y=x2﹣3x+2如图所示，由图象可知：

当x＜1或x＞2时，y＞0所以一元二次不等式x2﹣3x+2＞0的解集为x＜1或x＞2

(1)填空：x2﹣3x+2＜0的解集为　   　；x2﹣3x≥0的解集为　   　．

(2)用类似的方法解一元二次不等式：﹣x2﹣2x+3＞0．

29．先阅读，再解题.

例题:解一元二次不等式 (x+3)(x-3)>0

解:因为 (x+3)(x-3)>0.

由有理数的乘法法则“两数相乘,同号得正”，

所以有    或 

解不等式组①,得x>3,

解不等式组②,得x<-3.

故(x+3)(x-3)>0的解集为x>3或x<-3．

即一元二次不等式(x+3)(x-3)>0的解集为x>3或x<-3．

问题:求不等式的解集.

30．阅读材料，解答问题．

例：用图象法解一元二次不等式：x2﹣2x﹣3＞0

解：设y=x2﹣2x﹣3，则y是x的二次函数．∵a=1＞0，∴抛物线开口向上．

又∵当y=0时，x2﹣2x﹣3=0，解得x1=﹣1，x2=3．

∴由此得抛物线y=x2﹣2x﹣3的大致图象如图所示．

观察函数图象可知：当x＜﹣1或x＞3时，y＞0．

∴x2﹣2x﹣3＞0的解集是：x＜﹣1或x＞3．

(1)观察图象，直接写出一元二次不等式：x2﹣2x﹣3＞0的解集是　________ ；   

(2)仿照上例，用图象法解一元二次不等式：x2﹣1＞0．