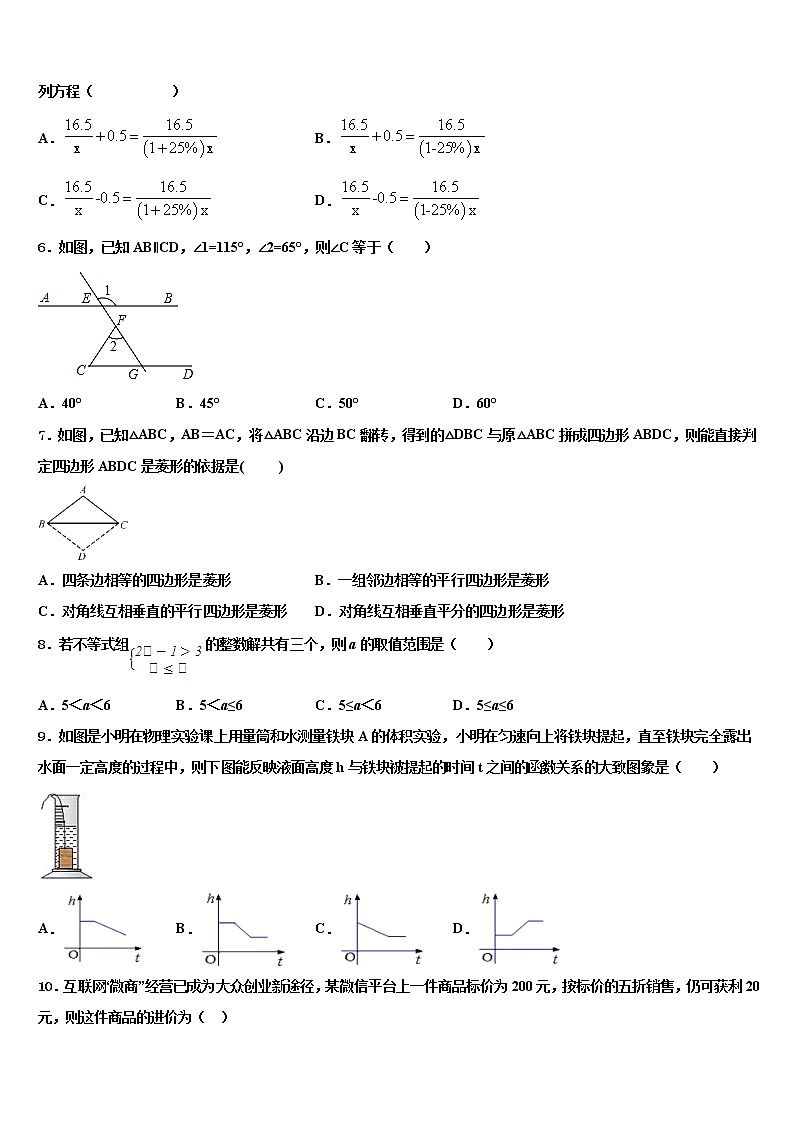
2021-2022学年黑龙江省牡丹江市达标名校中考数学最后一模试卷含解析

2021-2022中考数学模拟试卷

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。

2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。

4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）

1．下列图形中，既是中心对称图形又是轴对称图形的是（　　）

A． B．

C． D．

2．自1993年起，联合国将每年的3月11日定为“世界水日”，宗旨是唤起公众的节水意识，加强水资源保护．某校在开展“节约每一滴水”的活动中，从初三年级随机选出10名学生统计出各自家庭一个月的节约用水量，有关数据整理如下表．

这组数据的中位数和众数分别是（  ）

A．1.1，1.1； B．1.4，1.1； C．1.3，1.4； D．1.3，1.1．

3．有理数a、b在数轴上的位置如图所示，则下列结论中正确的是（　　）

A．a+b＞0 B．ab＞0 C．a﹣b＜o D．a÷b＞0

4．﹣22×3的结果是（　　）

A．﹣5 B．﹣12 C．﹣6 D．12

5．小宇妈妈上午在某水果超市买了 16.5 元钱的葡萄，晚上散步经过该水果超市时，发现同一批葡萄的价格降低了 25％ ，小宇妈妈又买了 16.5 元钱的葡萄，结果恰好比早上多了 0.5 千克．若设早上葡萄的价格是 x 元/千克，则可列方程（           ）

A． B．

C． D．

6．如图，已知AB∥CD，∠1=115°，∠2=65°，则∠C等于（　　）

A．40° B．45° C．50° D．60°

7．如图，已知△ABC，AB＝AC，将△ABC沿边BC翻转，得到的△DBC与原△ABC拼成四边形ABDC，则能直接判定四边形ABDC是菱形的依据是(     )

A．四条边相等的四边形是菱形 B．一组邻边相等的平行四边形是菱形

C．对角线互相垂直的平行四边形是菱形 D．对角线互相垂直平分的四边形是菱形

8．若不等式组的整数解共有三个，则a的取值范围是（　　）

A．5＜a＜6 B．5＜a≤6 C．5≤a＜6 D．5≤a≤6

9．如图是小明在物理实验课上用量筒和水测量铁块A的体积实验，小明在匀速向上将铁块提起，直至铁块完全露出水面一定高度的过程中，则下图能反映液面高度h与铁块被提起的时间t之间的函数关系的大致图象是（　　）

A． B． C． D．

10．互联网“微商”经营已成为大众创业新途径，某微信平台上一件商品标价为200元，按标价的五折销售，仍可获利20元，则这件商品的进价为（  ）

A．120元 B．100元 C．80元 D．60元

二、填空题（共7小题，每小题3分，满分21分）

11．从“线段，等边三角形，圆，矩形，正六边形”这五个图形中任取一个，取到既是轴对称图形又是中心对称图形的概率是_____．

12．如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作AE⊥BD，垂足为点E，若∠EAC=2∠CAD，则∠BAE=__________度．

13．我国经典数学著作《九章算术》中有这样一道名题，就是“引葭赴岸”问题，（如图）题目是：“今有池方一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐，问水深，葭长各几何？”

题意是：有一正方形池塘，边长为一丈，有棵芦苇长在它的正中央，高出水面部分有一尺长，把芦苇拉向岸边，恰好碰到岸沿，问水深和芦苇长各是多少？（小知识：1丈=10尺）

如果设水深为x尺，则芦苇长用含x的代数式可表示为       尺，根据题意列方程为        ．

14．已知点A（2，4）与点B（b﹣1，2a）关于原点对称，则ab＝_____．

15．一个凸多边形的内角和与外角和相等，它是______边形．

16．分解因式：________．

17．如图，在边长为4的菱形ABCD中，∠A=60°，M是AD边的中点，点N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，则线段A′C长度的最小值是______．

三、解答题（共7小题，满分69分）

18．（10分）某中学九年级甲、乙两班商定举行一次远足活动，、两地相距10千米，甲班从地出发匀速步行到地，乙班从地出发匀速步行到地.两班同时出发，相向而行.设步行时间为小时，甲、乙两班离地的距离分别为千米、千米，、与的函数关系图象如图所示，根据图象解答下列问题：直接写出、与的函数关系式；求甲、乙两班学生出发后，几小时相遇？相遇时乙班离地多少千米？甲、乙两班相距4千米时所用时间是多少小时?

19．（5分）如图，AD是△ABC的中线，过点C作直线CF∥AD．

（问题）如图①，过点D作直线DG∥AB交直线CF于点E，连结AE，求证：AB＝DE．

（探究）如图②，在线段AD上任取一点P，过点P作直线PG∥AB交直线CF于点E，连结AE、BP，探究四边形ABPE是哪类特殊四边形并加以证明．

（应用）在探究的条件下，设PE交AC于点M．若点P是AD的中点，且△APM的面积为1，直接写出四边形ABPE的面积．

20．（8分）如图，四边形ABCD，AD∥BC，DC⊥BC于C点，AE⊥BD于E，且DB＝DA．求证：AE＝CD．

21．（10分）如图，抛物线交X轴于A、B两点，交Y轴于点C ，．

（1）求抛物线的解析式；

（2）平面内是否存在一点P，使以A，B，C，P为顶点的四边形为平行四边形，若存在直接写出P的坐标，若不存在请说明理由。

22．（10分）如图，直线y1=﹣x+4，y2=x+b都与双曲线y=交于点A（1，m），这两条直线分别与x轴交于B，C两点．

（1）求y与x之间的函数关系式；

（2）直接写出当x＞0时，不等式x+b＞的解集；

（3）若点P在x轴上，连接AP把△ABC的面积分成1：3两部分，求此时点P的坐标．

23．（12分）京沈高速铁路赤峰至喀左段正在建设中，甲、乙两个工程队计划参与一项工程建设，甲队单独施工30天完成该项工程的，这时乙队加入，两队还需同时施工15天，才能完成该项工程．若乙队单独施工，需要多少天才能完成该项工程?若甲队参与该项工程施工的时间不超过36天，则乙队至少施工多少天才能完成该项工程?

24．（14分）解方程

参考答案

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）

1、D

【解析】
根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形，以及轴对称图形的定义即可判断出．

【详解】

解：A. ∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，是轴对称图形，故此选项错误；

B. ∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，不是轴对称图形，故此选项错误；

C. ∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，是轴对称图形，故此选项错误；

D. ∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，也是轴对称图形，故此选项正确.

故选：D.

【点睛】

本题考查了中心对称图形与轴对称图形的定义，解题的关键是熟练的掌握中心对称图形与轴对称图形的定义.

2、D

【解析】

分析：中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数，众数是一组数据中出现次数最多的数据，注意众数可以不止一个．

详解：这组数据的中位数是；

    这组数据的众数是1.1．

    故选D．

点睛：本题属于基础题，考查了确定一组数据的中位数和众数的能力，要明确定义，一些学生往往对这个概念掌握不清楚，计算方法不明确而误选其它选项，注意找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数，如果数据有奇数个，则正中间的数字即为所求，如果是偶数个则找中间两位数的平均数．

3、C

【解析】
利用数轴先判断出a、b的正负情况以及它们绝对值的大小，然后再进行比较即可．

【详解】

解：由a、b在数轴上的位置可知：a＜1，b＞1，且|a|＞|b|，

∴a+b＜1，ab＜1，a﹣b＜1，a÷b＜1．

故选：C．

4、B

【解析】
先算乘方，再算乘法即可．

【详解】

解：﹣22×3＝﹣4×3＝﹣1．

故选：B．

【点睛】

本题主要考查了有理数的混合运算，熟练掌握法则是解答本题的关键．有理数的混合运算，先乘方，再乘除，后加减，有括号的先算括号内的．

5、B

【解析】

分析：根据数量=，可知第一次买了千克，第二次买了，根据第二次恰好比第一次多买了 0.5 千克列方程即可.

详解：设早上葡萄的价格是 x 元/千克，由题意得，

.

故选B.

点睛：本题考查了分式方程的实际应用，解题的关键是读懂题意，找出列方程所用到的等量关系.

6、C

【解析】

分析：根据两直线平行，同位角相等可得 再根据三角形内角与外角的性质可得∠C的度数．

详解：∵AB∥CD，

∴

∵

∴

故选C.

点睛：考查平行线的性质和三角形外角的性质，三角形的一个外角等于与它不相邻的两个内角的和.

7、A

【解析】
根据翻折得出AB=BD，AC=CD，推出AB=BD=CD=AC，根据菱形的判定推出即可．

【详解】

∵ 将 △ABC 延底边 BC 翻折得到 △DBC ，

∴AB=BD ， AC=CD ，

∵AB=AC ，

∴AB=BD=CD=AC ，

∴ 四边形 ABDC 是菱形；

故选A.

【点睛】

本题考查了菱形的判定方法：四边都相等的四边形是菱形；对角线互相垂直的平行四边形是菱形；有一组邻边相等的平行四边形是菱形.

8、C

【解析】
首先确定不等式组的解集，利用含a的式子表示，根据整数解的个数就可以确定有哪些整数解，根据解的情况可以得到关于a的不等式，从而求出a的范围．

【详解】

解不等式组得：2＜x≤a，

∵不等式组的整数解共有3个，

∴这3个是3，4，5，因而5≤a＜1．

故选C．

【点睛】

本题考查了一元一次不等式组的整数解，正确解出不等式组的解集，确定a的范围，是解答本题的关键．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．

9、B

【解析】

根据题意，在实验中有3个阶段，

①、铁块在液面以下，液面得高度不变；

②、铁块的一部分露出液面，但未完全露出时，液面高度降低；

③、铁块在液面以上，完全露出时，液面高度又维持不变；

分析可得，B符合描述；

故选B．

10、C

【解析】
解：设该商品的进价为x元/件，

依题意得：（x+20）÷=200，解得：x=1．

∴该商品的进价为1元/件．

故选C．

二、填空题（共7小题，每小题3分，满分21分）

11、.

【解析】
试题分析：在线段、等边三角形、圆、矩形、正六边形这五个图形中，既是中心对称图形又是轴对称图形的有线段、圆、矩形、正六边形，共4个，所以取到的图形既是中心对称图形又是轴对称图形的概率为.

【点睛】

本题考查概率公式，掌握图形特点是解题关键，难度不大.

12、22.5°

【解析】
四边形ABCD是矩形，

AC=BD，OA=OC，OB=OD，

OA=OB═OC，

∠OAD=∠ODA，∠OAB=∠OBA，

∠AOE=∠OAD+∠ODA=2∠OAD，

∠EAC=2∠CAD，

∠EAO=∠AOE，

AE⊥BD，

∠AEO=90°，

∠AOE=45°，

∠OAB=∠OBA=67.5°，

即∠BAE=∠OAB﹣∠OAE=22.5°．

考点：矩形的性质；等腰三角形的性质．

13、（x+1）；.

【解析】

试题分析：设水深为x尺，则芦苇长用含x的代数式可表示为（x+1）尺，根据题意列方程为.

故答案为（x+1），.

考点：由实际问题抽象出一元二次方程；勾股定理的应用．

14、1．

【解析】

由题意，得

b−1=−1，1a=−4，

解得b=−1，a=−1，

∴ab=(−1) ×(−1)=1，

故答案为1.

15、四

【解析】
任何多边形的外角和是360度，因而这个多边形的内角和是360度．n边形的内角和是（n-2）•180°，如果已知多边形的内角和，就可以得到一个关于边数的方程，解方程就可以求出多边形的边数．

【详解】

解：设边数为n，根据题意，得

（n-2）•180=360，

解得n=4，则它是四边形．

故填：四.

【点睛】

此题主要考查已知多边形的内角和求边数，可以转化为方程的问题来解决．

16、 (a+1)(a-1)

【解析】
根据平方差公式分解即可.

【详解】

(a+1)(a-1).

故答案为：(a+1)(a-1).

【点睛】

本题考查了因式分解，把一个多项式化成几个整式的乘积的形式，叫做因式分解.因式分解常用的方法有：①提公因式法；②公式法；③十字相乘法；④分组分解法. 因式分解必须分解到每个因式都不能再分解为止.

17、

【解析】
解：如图所示：∵MA′是定值，A′C长度取最小值时，即A′在MC上时，

过点M作MF⊥DC于点F，

∵在边长为2的菱形ABCD中，∠A=60°，M为AD中点，

∴2MD=AD=CD=2，∠FDM=60°，

∴∠FMD=30°，

∴FD=MD=1，

∴FM=DM×cos30°=，

∴，

∴A′C=MC﹣MA′=．

故答案为．

【点评】

此题主要考查了菱形的性质以及锐角三角函数关系等知识，得出A′点位置是解题关键．

三、解答题（共7小题，满分69分）

18、（1）y1=4x，y2=-5x+1．（2）km．（3）h．

【解析】
（1）由图象直接写出函数关系式；

（2）若相遇，甲乙走的总路程之和等于两地的距离.

【详解】

(1)根据图可以得到甲2.5小时,走1千米,则每小时走4千米,则函数关系是：y1=4x，

乙班从B地出发匀速步行到A地,2小时走了1千米,则每小时走5千米,则函数关系式是：y2=−5x+1.

(2)由图象可知甲班速度为4km/h，乙班速度为5km/h，

设甲、乙两班学生出发后，x小时相遇，则

4x+5x=1，

解得x=.

当x=时,y2=−5×+1=，

∴相遇时乙班离A地为km.

(3)甲、乙两班首次相距4千米，

即两班走的路程之和为6km，

故4x+5x=6，

解得x=h.

∴甲、乙两班首次相距4千米时所用时间是h.

19、【问题】：详见解析；【探究】：四边形ABPE是平行四边形，理由详见解析；【应用】：8.

【解析】
（1）先根据平行线的性质和等量代换得出∠1＝∠3，再利用中线性质得到BD＝DC，证明△ABD≌△EDC，从而证明AB＝DE（2）方法一：过点D作DN∥PE交直线CF于点N，由平行线性质得出四边形PDNE是平行四边形，从而得到四边形ABPE是平行四边形.方法二: 延长BP交直线CF于点N，根据平行线的性质结合等量代换证明△ABP≌△EPN，

从而证明四边形ABPE是平行四边形（3）延长BP交CF于H，根据平行四边形的性质结合三角形的面积公式求解即可.

【详解】

证明：如图①

是的中线，

（或证明四边形ABDE是平行四边形，从而得到）

【探究】

四边形ABPE是平行四边形．

方法一：如图②，

证明：过点D作交直线于点，

∴四边形是平行四边形，

∵由问题结论可得

∴四边形是平行四边形．

方法二：如图③，

证明：延长BP交直线CF于点N，

∵是的中线，

∴四边形是平行四边形．

【应用】

如图④，延长BP交CF于H．

由上面可知，四边形是平行四边形，

∴四边形APHE是平行四边形，

，

【点睛】

此题重点考查学生对平行线性质，平行四边形性质的综合应用能力，熟练掌握平行线的性质是解题的关键.

20、证明见解析.

【解析】
由AD∥BC得∠ADB＝∠DBC,根据已知证明△AED≌△DCB（AAS）,即可解题.

【详解】

解：∵AD∥BC

∴∠ADB＝∠DBC

∵DC⊥BC于点C，AE⊥BD于点E

∴∠C＝∠AED＝90°

又∵DB＝DA

∴△AED≌△DCB（AAS）

∴AE＝CD

【点睛】

本题考查了三角形全等的判定和性质,属于简单题,证明三角形全等是解题关键.

21、（1）；（2） （3，-4） 或（5,4）或（-5,4）

【解析】
（1）设|OA|=1，确定A,B,C三点坐标，然后用待定系数法即可完成；

（2）先画出存在的点，然后通过平移和计算确定坐标；

【详解】

解：（1）设|OA|=1，则A(-1，0)，B(4，0)C（0,4）

设抛物线的解析式为y=ax2+bx+c

则有： 解得

所以函数解析式为：

（2）存在，（3，-4） 或（5,4）或（-5,4）

理由如下：如图：

P1相当于C点向右平移了5个单位长度，则坐标为（5，4）；

P2相当于C点向左平移了5个单位长度，则坐标为（-5，4）；

设P3坐标为（m，n）在第四象限，要使A P3BC是平行四边形，

则有A P3=BC, B P3=AC

∴ 即 （舍去）

P3坐标为（3，-4）

【点睛】

本题主要考查了二次函数综合题，此题涉及到待定系数法求二次函数解析式，通过作图确认平行四边形存在，然后通过观察和计算确定P点坐标；解题的关键在于规范作图，以便于树形结合.

22、（1）；（2）x＞1；（3）P（﹣，0）或（，0）

【解析】

分析：（1）求得A（1，3），把A（1，3）代入双曲线y=，可得y与x之间的函数关系式；

（2）依据A（1，3），可得当x＞0时，不等式x+b＞的解集为x＞1；

（3）分两种情况进行讨论，AP把△ABC的面积分成1：3两部分，则CP=BC=，或BP=BC=，即可得到OP=3﹣=，或OP=4﹣=，进而得出点P的坐标．

详解：（1）把A（1，m）代入y1=﹣x+4，可得m=﹣1+4=3，

∴A（1，3），

把A（1，3）代入双曲线y=，可得k=1×3=3，

∴y与x之间的函数关系式为：y=；

（2）∵A（1，3），

∴当x＞0时，不等式x+b＞的解集为：x＞1；

（3）y1=﹣x+4，令y=0，则x=4，

∴点B的坐标为（4，0），

把A（1，3）代入y2=x+b，可得3=+b，

∴b=，

∴y2=x+，

令y2=0，则x=﹣3，即C（﹣3，0），

∴BC=7，

∵AP把△ABC的面积分成1：3两部分，

∴CP=BC=，或BP=BC=

∴OP=3﹣=，或OP=4﹣=，

∴P（﹣，0）或（，0）．

点睛：本题考查了反比例函数与一次函数的交点问题：求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点．

23、（1）乙队单独施工需要1天完成;（2）乙队至少施工l8天才能完成该项工程．

【解析】
（1）先求得甲队单独施工完成该项工程所需时间，设乙队单独施工需要x天完成该项工程，再根据“甲完成的工作量+乙完成的工作量=1”列方程解方程即可求解；

（2）设乙队施工y天完成该项工程，根据题意列不等式解不等式即可.

【详解】

（1）由题意知，甲队单独施工完成该项工程所需时间为1÷=90（天）．

设乙队单独施工需要x天完成该项工程，则

，

去分母，得x+1=2x．

解得x=1．

经检验x=1是原方程的解．

答：乙队单独施工需要1天完成．

（2）设乙队施工y天完成该项工程，则

1-

解得y≥2．

答：乙队至少施工l8天才能完成该项工程．

24、x=-1．

【解析】
解：方程两边同乘x-2，得2x=x-2+1

解这个方程，得x= -1

检验：x= -1时，x-2≠0

∴原方程的解是x= -1

首先去掉分母，观察可得最简公分母是（x﹣2），方程两边乘最简公分母，可以把分式方程转化为整式方程求解，然后解一元一次方程，最后检验即可求解