
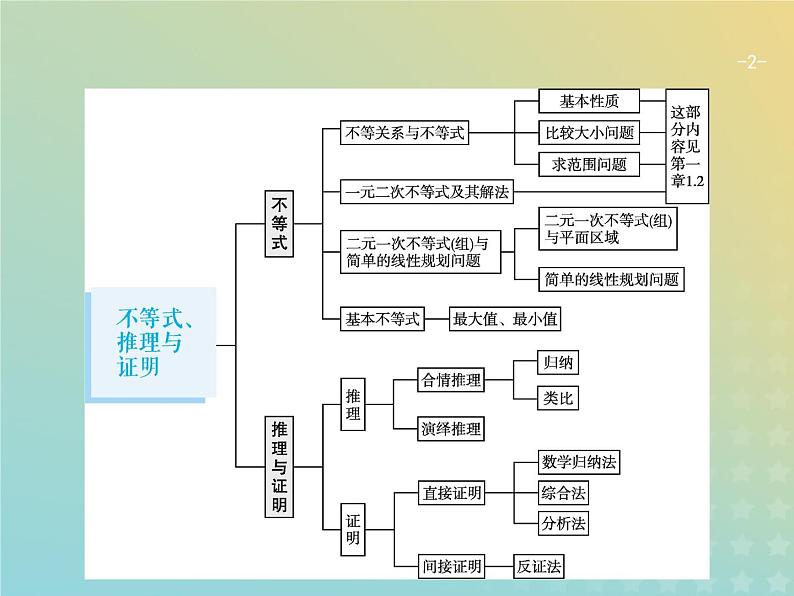





广西专用高考数学一轮复习第七章不等式推理与证明1二元一次不等式组与简单的线性规划问题课件新人教A版理
展开7.1 二元一次不等式(组) 与简单的线性规划问题
1.二元一次不等式表示的平面区域(1)一般地,二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的 .我们把直线画成虚线以表示区域 边界直线.当我们在平面直角坐标系中画不等式Ax+By+C≥0所表示的平面区域时,此区域应_____ 边界直线,则把边界直线画成 . (2)因为对直线Ax+By+C=0同一侧的所有点(x,y),把它的坐标(x,y)代入Ax+By+C,所得的符号都 ,所以只需在此直线的同一侧取一个特殊点(x0,y0)作为测试点,由Ax0+By0+C的 即可判断Ax+By+C>0表示的是直线Ax+By+C=0哪一侧的平面区域.
(3)利用“同号上,异号下”判断二元一次不等式表示的平面区域:①当B(Ax+By+C)>0时,区域为直线Ax+By+C=0的 ; ②当B(Ax+By+C)<0时,区域为直线Ax+By+C=0的 . 注:其中Ax+By+C的符号是给出的二元一次不等式的符号.(4)由几个不等式组成的不等式组所表示的平面区域,是各个不等式所表示的平面区域的公共部分.
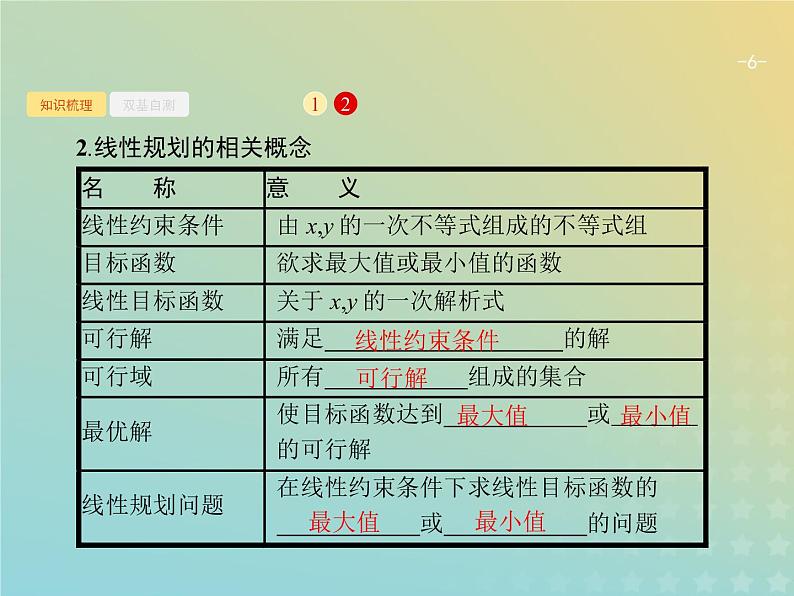
2.线性规划的相关概念
1.下列结论正确的打“√”,错误的打“×”.(1)不等式x-y-1>0表示的平面区域一定在直线x-y-1=0的上方.( )(2)两点(x1,y1),(x2,y2)在直线Ax+By+C=0异侧的充要条件是(Ax1+By1+C)(Ax2+By2+C)<0.( )(3)任何一个二元一次不等式组都表示平面上的一个区域.( )(4)在目标函数z=ax+by(b≠0)中,z的几何意义是直线ax+by-z=0在y轴上的截距.( )
2.若点(m,1)在不等式2x+3y-5>0所表示的平面区域内,则m的取值范围是( )A.m≥1B.m≤1C.m<1D.m>1
思考如何确定二元一次不等式(组)表示的平面区域?
解析:(1)如图,不等式组表示的平面区域是△AOC,当a从-2连续变化到1时,动直线x+y=a扫过Ω中的那部分区域为图中的四边形AODE,其面积为
解题心得确定二元一次不等式(组)表示的平面区域的方法:(1)“直线定界,特殊点定域”,即先作直线,再取特殊点并代入不等式组.若满足不等式组,则不等式(组)表示的平面区域为直线与特殊点同侧的那部分区域;否则就对应特殊点异侧的平面区域.(2)若不等式带等号,则边界为实线;若不等式不带等号,则边界为虚线.
(2)两条直线方程分别为x-2y+2=0与x+y-1=0.把x=0,y=0代入x-2y+2得2,可知直线x-2y+2=0右下方所表示的二元一次不等式为x-2y+2≥0,把x=0,y=0代入x+y-1得-1,可知直线x+y-1=0右上方所表示的二元一次不等式为x+y-1≥0,
考向一 求线性目标函数的最值
A.4B.6C.0D.2思考怎样利用可行域求线性目标函数的最值?
考向二 已知目标函数的最值求参数的取值A.[-1,2]B.[-2,1]C.[-3,-2]D.[-3,1]思考如何利用可行域及最优解求参数及其范围?
考向三 求非线性目标函数的最值
思考如何利用可行域求非线性目标函数最值?
解题心得1.利用可行域求线性目标函数最值的方法:首先利用约束条件作出可行域,然后根据目标函数找到最优解时的点,最后把解得点的坐标代入求解即可.2.若目标函数和约束条件都是线性的,且对应目标函数的最优解是可行域所对应图形的边界或顶点,则这时要求目标函数的最值只要把可行域的几个顶点代入,通过对比目标函数的对应函数值,即可取得最优解.
3.利用可行域及最优解求参数及其范围的方法:(1)若限制条件中含参数,依据参数的不同范围将各种情况下的可行域画出来,寻求最优解,确定参数的值;(2)若线性目标函数中含有参数,可对线性目标函数的斜率分类讨论,以此来确定线性目标函数经过哪个顶点取得最值,从而求出参数的值;也可以直接求出线性目标函数经过各顶点时对应的参数的值,然后进行检验,找出符合题意的参数值.4.利用可行域求非线性目标函数最值的方法:画出可行域,分析目标函数的几何意义是斜率问题还是距离问题,依据几何意义可求得最值.
所表示的平面区域(阴影部分),如图所示.由z=x-y,得y=x-z.由图可知当直线y=x-z经过可行域上的点B时,直线在y轴上的截距-z最小,此时z取得最大值.
(2)作出不等式组所表示的平面区域,即可行域,如图所示.
由已知得点A的坐标为(1,3),点C的坐标为(3,1).由图象可知直线DA的斜率最大,此时直线DA与直线x-y+2=0重合,即z的最大值为1.故选A.
例5某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时.生产一件产品A的利润为2 100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为 元. 思考求解线性规划的实际问题要注意什么?
目标函数z=2 100x+900y,画出约束条件对应的可行域,如图所示,阴影部分中的整数点就表示所有可能的生产安排.
解题心得求解线性规划的实际问题要注意两点:(1)设出未知数x,y,并写出问题中的约束条件和目标函数,注意约束条件中的不等式是否含有等号;(2)判断所设未知数x,y的取值范围,分析x,y是否为整数、非负数等.
对点训练3A,B两个居民小区的居委会欲组织本小区的中学生利用双休日去市郊的敬老院参加献爱心活动.两个小区每名同学的往返车费及服务老人的人数如下表:
根据安排,去敬老院的往返总车费不能超过37元,且B小区参加献爱心活动的同学比A小区的同学至少多1人,则接受服务的老人最多有 人.
广西专用高考数学一轮复习高考大题增分专项四高考中的立体几何课件新人教A版理: 这是一份广西专用高考数学一轮复习高考大题增分专项四高考中的立体几何课件新人教A版理,共41页。PPT课件主要包含了-2-,-3-,题型一,题型二,题型三,题型四,-4-,-5-,-6-,-7-等内容,欢迎下载使用。
广西专用高考数学一轮复习选修4_5不等式选讲课件新人教A版理: 这是一份广西专用高考数学一轮复习选修4_5不等式选讲课件新人教A版理,共37页。PPT课件主要包含了-2-,知识梳理,双基自测,a+b,ab≥0,-3-,-4-,-5-,-6-,-7-等内容,欢迎下载使用。
广西专用高考数学一轮复习第七章不等式推理与证明5数学归纳法课件新人教A版理: 这是一份广西专用高考数学一轮复习第七章不等式推理与证明5数学归纳法课件新人教A版理,共24页。PPT课件主要包含了-2-,知识梳理,双基自测,k+1,-3-,-4-,-5-,-6-,-7-,-8-等内容,欢迎下载使用。












