2020-2021学年湖北省武汉市武昌区高二（下）期末数学试卷

2020-2021学年湖北省武汉市武昌区高二（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．（5分）设集合，，则　　

A． B．， C．，， D．，，

2．（5分）复数的共轭复数是　　

A． B． C． D．

3．（5分）若，则的值为　　

A． B． C． D．

4．（5分）设，，，则，，的大小关系为　　

A． B． C． D．

5．（5分）如图是函数，，的部分图象，给出下列四种说法：

①函数的周期为；

②函数图象的一条对称轴方程为；

③函数的递减区间为；

④当时，函数的值域为．

其中，正确的说法是　　

A．①② B．①③ C．②③ D．③④

6．（5分）已知椭圆的左、右顶点分别为，，且以线段为直径的圆与直线相切，则的离心率为　　

A． B． C． D．

7．（5分）三棱锥的顶点均在一个半径为4的球面上，为等边三角形且其边长为6，则三棱锥体积的最大值为　　

A． B． C． D．

8．（5分）已知，，，则　　

A． B． C． D．

二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

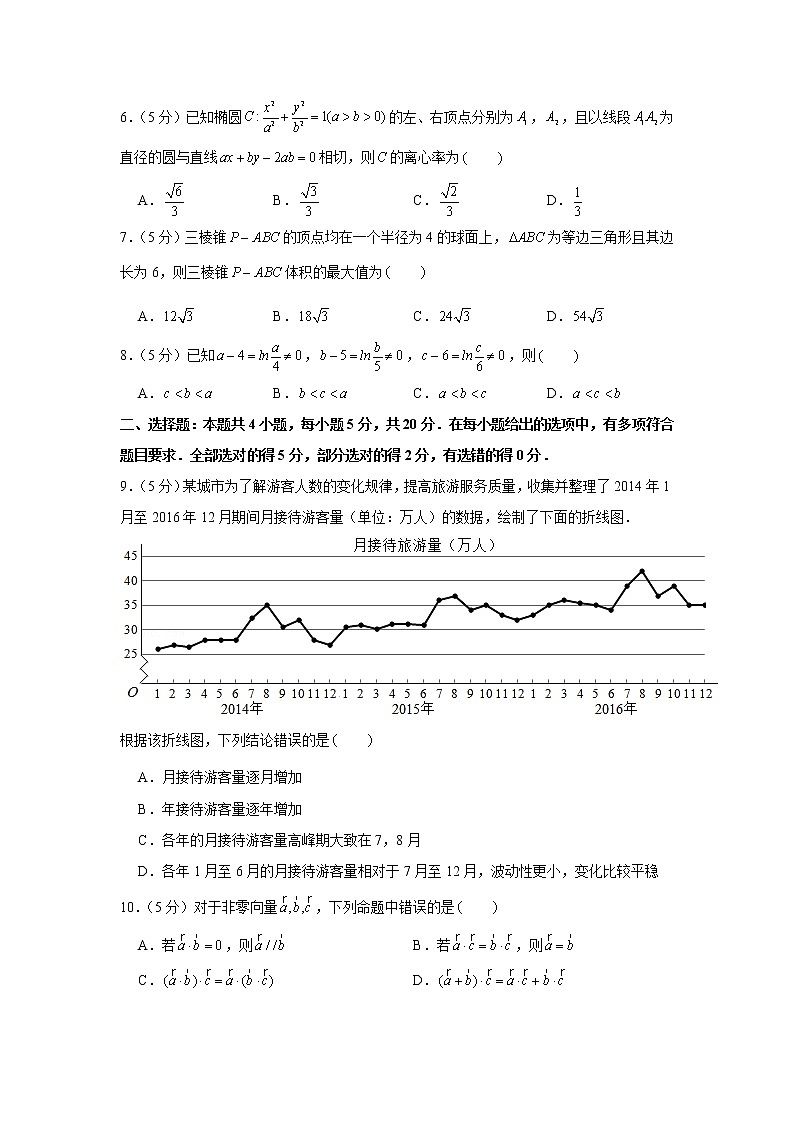
9．（5分）某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．

根据该折线图，下列结论错误的是　　

A．月接待游客量逐月增加 

B．年接待游客量逐年增加 

C．各年的月接待游客量高峰期大致在7，8月 

D．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳

10．（5分）对于非零向量，下列命题中错误的是　　

A．若，则 B．若，则 

C． D．

11．（5分）如图，透明塑料制成的长方体容器内灌进一些水，固定容器底面的一边于地面上，再将容器倾斜，随着倾斜度的不同，以下命题正确的是　　

A．有水的部分始终呈棱柱形 

B．水面所在四边形的面积为定值 

C．棱始终与水面所在平面平行 

D．当容器倾斜如图（3）所示时，是定值

12．（5分）已知双曲线的左，右焦点分别为，，过双曲线上的一点作两条渐近线的垂线，垂足分别为，，若，则　　

A．双曲线的离心率为 

B．四边形的面积为为坐标原点） 

C．双曲线的渐近线方程为 

D．直线与直线的斜率之积为定值

三、填空题：本题共4小题，每小题5分，共20分．

13．（5分）的展开式中，的系数为 　　．（用数字作答）

14．（5分）甲、乙、丙等5位同学随机站成一排合影留念，甲、乙两人相邻且甲站在丙的左侧，则不同的站法共有 　　种．（用数字作答）

15．（5分），，为三个不重合的平面，，，为三条不同的直线，给出下列命题：

①若，，则；

②若，，则；

③若，，则；

④若，，则．

其中正确命题的序号是 　　．

16．（5分）设函数，，其中，．若存在极值点，且，其中，则　　．

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

17．（10分）如图，，两点都在河的对岸（不可到达），为了测量，两点间的距离，在，两点的对岸选定两点，，测得，并且在点，两点分别测得，，，，试求，两点间的距离（精确到．

附：，，．

18．（12分）甲、乙两人各进行3次射击，甲每次击中目标的概率为，乙每次击中目标的概率，

（Ⅰ）记甲击中目标的次数为，求的概率分布及数学期望；

（Ⅱ）求甲恰好比乙多击中目标2次的概率．

19．（12分）已知数列是递增的等比数列，前3项和为7，且，，成等差数列．数列的首项为1，其前项和为，且．

（1）求数列和的通项公式；

（2）设，求数列的前项和．

20．（12分）如图，在四棱锥中，已知底面是等腰梯形，，，侧面是等边三角形，，点在平面上的射影恰是线段的中点．求：

（1）二面角的大小；

（2）异面直线与所成角的余弦值．

21．（12分）抛物线的方程为，过抛物线上一点，作斜率为，的两条直线分别交抛物线于，，，两点，，三点互不相同），且满足．

（1）若线段的中点为，证明线段的中点在轴上；

（2）若点的坐标为，求为钝角时点的纵坐标的取值范围．

22．（12分）已知函数．

（1）讨论函数零点的个数；

（2）若函数恰有两个零点，，证明：．

2020-2021学年湖北省武汉市武昌区高二（下）期末数学试卷

参考答案与试题解析

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．（5分）设集合，，则　　

A． B．， C．，， D．，，

【解答】解：集合，或，

．

故选：．

2．（5分）复数的共轭复数是　　

A． B． C． D．

【解答】解：，

复数的共轭复数是．

故选：．

3．（5分）若，则的值为　　

A． B． C． D．

【解答】解：，，

又，

，

．

故选：．

4．（5分）设，，，则，，的大小关系为　　

A． B． C． D．

【解答】解：，，

．

故选：．

5．（5分）如图是函数，，的部分图象，给出下列四种说法：

①函数的周期为；

②函数图象的一条对称轴方程为；

③函数的递减区间为；

④当时，函数的值域为．

其中，正确的说法是　　

A．①② B．①③ C．②③ D．③④

【解答】解：根据函数的图象：

，，

故，所以，

当时，，

故，故，

当时，，时，，

根据函数的图象，，

故，

对于①，函数的周期为，故①正确；

对于②，当时，，故②错误；

对于③，令，整理得：，故函数的递减区间为，故③正确；

④当时，故，函数的值域为，故④错误．

故选：．

6．（5分）已知椭圆的左、右顶点分别为，，且以线段为直径的圆与直线相切，则的离心率为　　

A． B． C． D．

【解答】解：以线段为直径的圆的圆心为坐标原点，半径为，圆的方程为，

直线与圆相切，所以圆心到直线的距离等于半径，

即，整理可得，

即，即，从而，

则椭圆的离心率，

故选：．

7．（5分）三棱锥的顶点均在一个半径为4的球面上，为等边三角形且其边长为6，则三棱锥体积的最大值为　　

A． B． C． D．

【解答】解：三棱锥是半径为4的球面上四点，为等边三角形，

所以，

球心为，三角形 的外心为，显然是的延长线与球的交点，如图所示：

计算，，

所以三棱锥高的最大值为，

所以三棱锥体积的最大值为．

故选：．

8．（5分）已知，，，则　　

A． B． C． D．

【解答】解：设，

求导可得，

在单调递减，在单调递增，

，

，

（a）（4），

同理可得（b）（5），（c）（6），

当时，，且在单调递减，

，，，

又（4）（5）（6），

（a）（b）（c），

又在单调递减，

．

故选：．

二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

9．（5分）某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．

根据该折线图，下列结论错误的是　　

A．月接待游客量逐月增加 

B．年接待游客量逐年增加 

C．各年的月接待游客量高峰期大致在7，8月 

D．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳

【解答】解：由已有中2014年1月至2016年12月期间月接待游客量（单位：万人）的数据可得：

月接待游客量逐月有增有减，故错误；

年接待游客量逐年增加，故正确；

各年的月接待游客量高峰期大致在7，8月，故正确；

各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳，故正确；

故选：．

10．（5分）对于非零向量，下列命题中错误的是　　

A．若，则 B．若，则 

C． D．

【解答】解：选项，，由是非零向量，所以，，故，所以，即，故错误；

选项，，，

，不能得到，故错误；

选项，表示与共线的向量，表示与共线的向量，故错误；

选项，由平面向量数量积运算律可知，正确；

故选：．

11．（5分）如图，透明塑料制成的长方体容器内灌进一些水，固定容器底面的一边于地面上，再将容器倾斜，随着倾斜度的不同，以下命题正确的是　　

A．有水的部分始终呈棱柱形 

B．水面所在四边形的面积为定值 

C．棱始终与水面所在平面平行 

D．当容器倾斜如图（3）所示时，是定值

【解答】解：由棱柱的特征：有两个平面时相互平行且是全等的多边形，其余每相邻两个面的交线也相互平行，而这些面都是平行四边形，

故选项正确；

因为睡眠所在四边形的面积，从图2，图3可以发现，有条边长不变，而另外一条长随着倾斜度变化而变化，

所以所在四边形的面积是变化的，

故选项错误；

因为棱始终与是平行的，与平面始终平行，

故选项正确；

因为水的体积是不变的，高始终是也不变，则底面也不变，即是定值，

故选项正确．

故选：．

12．（5分）已知双曲线的左，右焦点分别为，，过双曲线上的一点作两条渐近线的垂线，垂足分别为，，若，则　　

A．双曲线的离心率为 

B．四边形的面积为为坐标原点） 

C．双曲线的渐近线方程为 

D．直线与直线的斜率之积为定值

【解答】解：双曲线的两条渐近线分别为和，

设，，则

所以，

又点在双曲线上，则，

所以，

因为，所以，

即，

又，所以，故正确；

因为，

所以，所以，所以四边形是矩形，

故四边形的面积为，故正确；

因为，所以双曲线的渐近线方程为，故错误；

，故正确．

故选：．

三、填空题：本题共4小题，每小题5分，共20分．

13．（5分）的展开式中，的系数为 　60　．（用数字作答）

【解答】解：的通项公式为：．

令，得．

可得项的系数为，

故答案为：60．

14．（5分）甲、乙、丙等5位同学随机站成一排合影留念，甲、乙两人相邻且甲站在丙的左侧，则不同的站法共有 　24　种．（用数字作答）

【解答】解：根据题意，分2步进行分析：

①将除甲乙丙之外的2人全排列，有种情况，

②将甲乙看成一个整体，和丙一起安排在空位中，有种情况，

则有种不同的站法；

故答案为：24，

15．（5分），，为三个不重合的平面，，，为三条不同的直线，给出下列命题：

①若，，则；

②若，，则；

③若，，则；

④若，，则．

其中正确命题的序号是 　①④　．

【解答】解：①若，，由平行公理可得，故①正确；

②若，，则或与相交或与异面，故②错误；

③若，，则或与相交，故③错误；

④若，，由平面与平面平行的传递性可得，故④正确．

故答案为：①④．

16．（5分）设函数，，其中，．若存在极值点，且，其中，则　4　．

【解答】解：，，

因为是极值点，所以，即，又即，

因为，所以，

即，因为，

所以，

把代入化简得，因为，

所以，即．

故答案为：4．

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

17．（10分）如图，，两点都在河的对岸（不可到达），为了测量，两点间的距离，在，两点的对岸选定两点，，测得，并且在点，两点分别测得，，，，试求，两点间的距离（精确到．

附：，，．

【解答】解：在中，，，，

所以，是直角三角形，求得．

在中，，，所以．

由正弦定理，得，所以．

在中，，由余弦定理，得，

所以，，两点间的距离为．

18．（12分）甲、乙两人各进行3次射击，甲每次击中目标的概率为，乙每次击中目标的概率，

（Ⅰ）记甲击中目标的次数为，求的概率分布及数学期望；

（Ⅱ）求甲恰好比乙多击中目标2次的概率．

【解答】解：（Ⅰ）由题意知的可能取值是0，1，2，3

，，

，，

的概率分布如下表：

，

（或；

（Ⅱ）设甲恰比乙多击中目标2次为事件，

甲恰击中目标2次且乙恰击中目标0次为事件，甲恰击中目标3次且乙恰击中目标1次为事件，

则，，为互斥事件．

甲恰好比乙多击中目标2次的概率为

19．（12分）已知数列是递增的等比数列，前3项和为7，且，，成等差数列．数列的首项为1，其前项和为，且．

（1）求数列和的通项公式；

（2）设，求数列的前项和．

【解答】解：（1）设等比数列的公比为，

因为前3项和为7，且，，成等差数列，

所以，（其中舍去），

所以数列的通项公式为；

因为，

所以，

两式相减，得，

化简得，

于是，

所以；

（2）由（1）知，，

则，

所以，

故，

所以．

20．（12分）如图，在四棱锥中，已知底面是等腰梯形，，，侧面是等边三角形，，点在平面上的射影恰是线段的中点．求：

（1）二面角的大小；

（2）异面直线与所成角的余弦值．

【解答】解：设，则，

（1）如图，取的中点，连接，，

因为是等腰梯形，且为的中点，

所以于．

因为是等边三角形，为的中点，

所以于．

所以是二面角的平面角．

点在平面上的射影为，

，．

于是中，，所以．

即二面角的大小是．

（2）过作的平行线交于，则等于异面直线与所成的角．

由是平行四边形，得．

在中，．

在中，．

在中，由余弦定理得，

异面直线与所成角的余弦值为．

21．（12分）抛物线的方程为，过抛物线上一点，作斜率为，的两条直线分别交抛物线于，，，两点，，三点互不相同），且满足．

（1）若线段的中点为，证明线段的中点在轴上；

（2）若点的坐标为，求为钝角时点的纵坐标的取值范围．

【解答】解：（1）证明：设直线的方程为，直线的方程为，

点，和点，的坐标是方程组的解，

消去，整理得，

于是，即，同理可得，，

因为，所以，

因为线段的中点为，所以，

因为，所以线段的中点在轴上；

（2）由（1）知，当点的坐标为时，，

代入，求得，同理可得，，

因此直线、分别与抛物线的交点、的坐标为

，，

于是，，

所以，

因为为钝角且、、三点互不相同，

所以，即，

解得或，

又，所以当时，；

当时，，

综上所述，为钝角时点的纵坐标的取值范围为．

22．（12分）已知函数．

（1）讨论函数零点的个数；

（2）若函数恰有两个零点，，证明：．

【解答】解：（1）．

当时，；当时，．

所以，函数在单调递增；在单调递减．

所以，当时，有最大值．

当时，，函数无零点；

当时，，函数有1个零点：

当时，，，（a），（a）．

当时，（a）；当时，（a）．

所以，（a）在单调递增，在单调递减．

所以，即（a）．

所以在和各有一个零点，即有两个零点．

综上，当时，函数无零点；

当时，函数有1个零点；当时，有两个零点．

（2）证明：由（1）知，函数恰有两个零点时，，且．

要证，只需证．

因为在单调递减，所以只需证．

因为，所以只需证，其中．

令，，

则，

所以，因为，

所以在单调递增，从而，

所以在单调递减，所以，即，

于是，所以．

声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2022/6/14 16:52:15；用户：13159259195；邮箱：13159259195；学号：39016604