2021-2022学年福建省建瓯第一中学高二下学期第一次月考数学试题（解析版）

2021-2022学年福建省建瓯第一中学高二下学期第一次月考数学试题

一、单选题

1．函数的定义域为（       ）

A． B． C． D．

【答案】B

【分析】根据偶次根式被开方数非负，对数的真数大于零可得出关于实数的不等式，进而可求得原函数的定义域.

【详解】对于函数，有，解得.

因此，函数的定义域为.

故选：B.

【点睛】本题考查具体函数定义域的求解，考查计算能力，属于基础题.

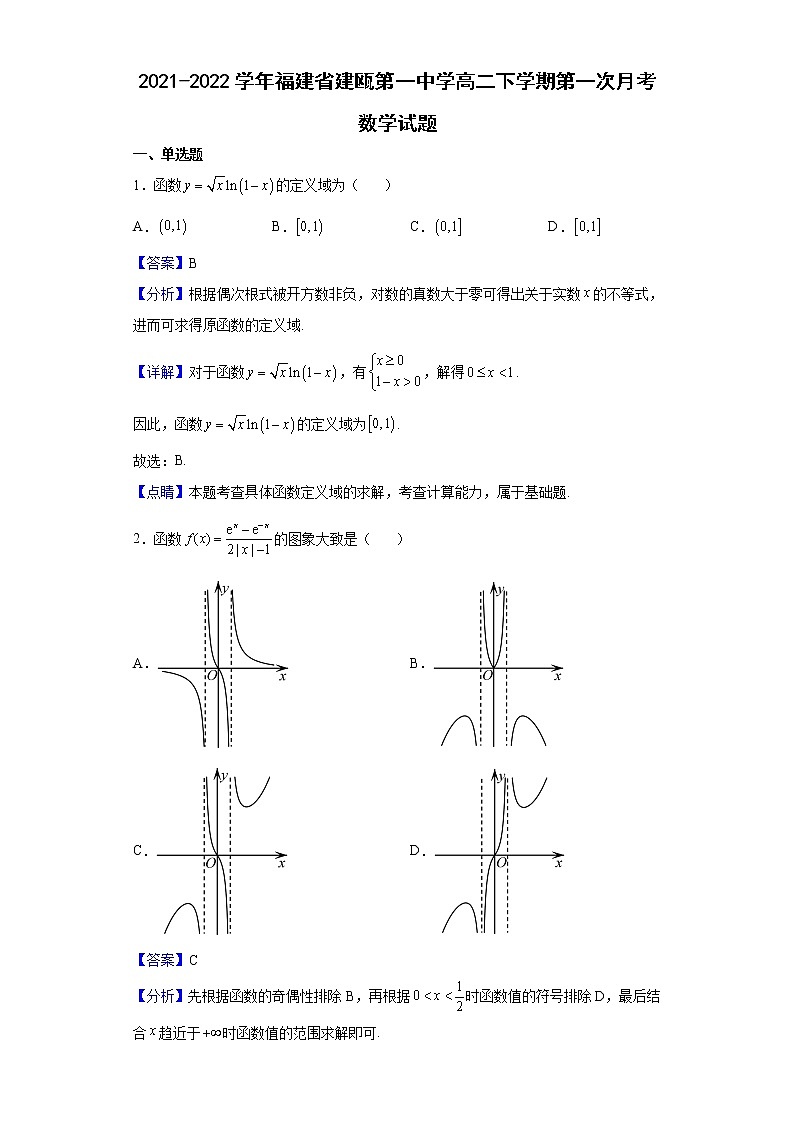
2．函数的图象大致是（       ）

A． B．

C． D．

【答案】C

【分析】先根据函数的奇偶性排除B，再根据时函数值的符号排除D，最后结合趋近于时函数值的范围求解即可.

【详解】解：函数的定义域为，，

所以函数为奇函数，图像关于原点对称，排除B选项，

因为当时，，

所以当时，，时，，故排除D，

当趋近于时，由于指数呈爆炸型增长，故函数值趋近于，故排除A选项，

故选：C

3．已知随机变量，若，则，分别是(   　)

A．4和2.4 B．2和2.4 C．6和2.4 D．4和5.6

【答案】A

【详解】

故选A．

4．二项式的展开式中的项的系数为（       ）

A．240 B．80 C． D．

【答案】C

【分析】写出二项式的展开式，从而可得的展开式中的系数.

【详解】因为二项式的展开式为：，

所以的展开式中含的项为，

则的系数为，

故选：C.

5．6名同学到甲、乙、丙三个场馆做志愿者，每名同学只去1个场馆，甲场馆安排1名，乙场馆安排2名，丙场馆安排3名，则不同的安排方法共有（       ）

A．120种 B．90种

C．60种 D．30种

【答案】C

【分析】分别安排各场馆的志愿者，利用组合计数和乘法计数原理求解.

【详解】首先从名同学中选名去甲场馆，方法数有；

然后从其余名同学中选名去乙场馆，方法数有；

最后剩下的名同学去丙场馆.

故不同的安排方法共有种.

故选：C

【点睛】本小题主要考查分步计数原理和组合数的计算，属于基础题.

6．已知n是一个三位正整数，若n的十位数字大于个位数字，百位数字大于十位数字，则称n为三位递增数.己知，设事件A为“由a，b，c组成三位正整数(数字可重复)”，事件B为“由a，b，c组成的三位正整数为递增数”则(       )

A． B． C． D．

【答案】B

【分析】根据条件概率计算公式即可计算.

【详解】由题可知n(A)＝4×5×5＝100，

由a，b，c组成的三位正整数为递增数，则：

若该三位数个位是0，则百位和十位从1，2，3，4四个数字中任选两个按大小排列即可，共种可能；

若该三位数个位是1，则百位和十位从2，3，4三个数字中任选两个按大小排列即可，共种可能；

若该三位数个位是2，则百位为4，十位为3，共1种可能；

故n(AB)＝6＋3＋1＝10，

故.

故选：B.

7．设集合，那么集合中满足条件

“”的元素个数为

A． B． C． D．

【答案】D

【详解】试题分析：分以下三种情况讨论，

（1），则上述五个数中有一个为或，其余四个数为零，此时集合有

个元素；

（2），则上述五个数中有两个数为或，其余三个数为零，其中这两个数的所有可能搭配有中，此时集合有个；

（3），则上述五个数中有三个数为或，其余两个数为零，其中这两个数的所有可能搭配有中，此时集合有个；

综上所述，集合共有个元素.故选D.

【考点定位】

本题考查分类计数原理，属于较难题.

8．已知随机变量满足，，其中.令随机变量，则（       ）

A． B．

C． D．

【答案】D

【分析】根据题意,列表求得随机变量及的分布列,可知均为两点分布.由两点分布的均值及方差表示出和,根据比较大小即可得解.

【详解】随机变量满足,,其中.

则随机变量的分布列为:

所以

随机变量,

所以当时,,当时,

所以随机变量的分布列如下表所示(当时,只有一个情况,概率为1):

则

当即,解得.所以A、B错误.

恒成立.

所以C错误,D正确

故选:D

【点睛】本题考查了随机变量的分布列,两点分布的特征及均值和方差求法,属于中档题.

二、多选题

9．下列结论正确的是（       ）

A． B．

C． D．

【答案】BC

【分析】根式的运算及根式与指数互化判断A、B；应用对数的运算性质判断C、D.

【详解】A：，故错误；B：，故正确；C：，故正确；D：，故错误.

故选：BC.

10．对于式子，下列说法正确的有（       ）

A．它的展开式中第4项的系数等于135

B．它的展开式中第3项的二项式系数为20

C．它的展开式中所有项系数之和为64

D．它的展开式中第一项的系数为

【答案】CD

【分析】根据的展开式的通项公式求解判断.

【详解】的展开式的通项公式是，

A.，所以第4项的系数等于-540，故错误；

B. ，所以它的展开式中第3项的二项式系数为15，故错误；

C. 令，得，所以它的展开式中所有项系数之和为64，故正确；

D. ，所以它的展开式中第一项的系数为，故正确；

故选：CD

11．某学生想在物理､化学､生物､政治､历史､地理､技术这七门课程中选三门作为选考科目，下列说法错误的是（       ）

A．若任意选择三门课程，选法总数为

B．若物理和化学至少选一门，选法总数为

C．若物理和历史不能同时选，选法总数为

D．若物理和化学至少选一门，且物理和历史不同时选，选法总数为20

【答案】AB

【分析】利用组合的概念可判断A，利用分类考虑，物理和化学只选一门、物理和化学都选，可判断B，利用间接法可判断C，若物理和化学至少选一门，有3种情况，分别讨论计算，可判断D．

【详解】对于A，若任意选择三门课程，选法总数为种，故A错误；

对于B，若物理和化学选一门，有种方法，其余两门从剩余的5门中选2门，有种选法，若物理和化学选两门，有种选法，剩下一门从剩余的5门中选1门，有种选法，

由分步乘法计数原理知，总数为种选法，故B错误；

对于C，若物理和历史不能同时选，选法总数为种，故C正确；

对于D，若物理和化学至少选一门，有3种情况，

只选物理不选历史，有种选法，

选化学，不选物理，有种选法，

物理与化学都选，不选历史，有种选法

故总数为种，故D正确.

故选：AB.

12．为了防止受到核污染的产品影响民众的身体健康，要求产品在进入市场前必须进行两轮核辐射检测，只有两轮都合格才能进行销售，否则不能销售.已知某产品第一轮检测不合格的概率为，第二轮检测不合格的概率为，两轮检测是否合格相互没有影响若产品可以销售，则每件产品获利40元；若产品不能销售，则每件产品亏损80元.已知一箱中有4件产品，记一箱产品获利元，则下列说法正确的是（       ）

A．该产品能销售的概率为

B．若表示一箱产品中可以销售的件数，则

C．若表示一箱产品中可以销售的件数，则

D．

【答案】ABD

【分析】根据题意先求出该产品能销售的概率，从而选项A可判断，由题意可得可判断选项B，根据独立重复事件的概率问题可判断C，D选项.

【详解】选项A. 该产品能销售的概率为,故选项A正确.

选项B. 由A 可得每件产品能销售的概率为

一箱中有4件产品，记一箱产品获利元，则，故选项B正确.

选项C. 由题意，不选项C不正确.

选项D. 由题意，即4件产品中有2件能销售，有2件产品不能销售.

 所以,故选项D正确.

故选：ABD

三、填空题

13．若函数且的图象恒过定点A，则A坐标为______．

【答案】

【分析】令，函数值是一个定值，与参数a无关，即可得到定点.

【详解】令，则，，

所以函数图象恒过定点为.

故答案为：

14．甲罐中有5个红球，2个白球和3个黑球，乙罐中有4个红球，3个白球和3个黑球，先从甲罐中随机取出一球放入乙罐，再从乙罐中随机取出一球，用B表示从乙罐中取出的球是红球的事件，则___________.

【答案】

【分析】根据互斥事件概率的乘法公式和条件概率的计算公式，带值计算即可.

【详解】由甲罐中随机取出一球放入乙罐，分别以表示取出的球是红球，白球和黑球的事件，

则是两两互斥的事件，且，

则.

故答案为：.

15．校园某处并排连续有6个停车位，现有3辆汽车需要停放，为了方便司机上下车，规定：当有汽车相邻停放时，车头必须同向；当车没有相邻时，车头朝向不限，则不同的停车方法共有__________种．（用数学作答）

【答案】528

【详解】(1)当三辆车都不相邻时有(种)

(2)当两辆车相邻时有(种)

(3)当三辆车相邻时有(种)

则共有(种)

点睛：本题考查了排列组合问题，由于本题里是三辆车有六个位置，所以情况较多，需要逐一列举出来，注意当三辆车都不相邻时的情况要考虑周全，容易漏掉一些情况，然后利用排列组合进行计算即可．

16．设函数，若是函数的最小值，则实数a的取值范围为___________.

【答案】

【分析】先由得到 ，再由时，的单调性，分，讨论求解.

【详解】解：当时，得到递增，且，

当时，，在上递减，在上递增，

若，，则在处取得最小值，不符合题意；

若，，则在处取得最小值，

若是函数在R上的最小值，

则，解得，

故答案为：

四、解答题

17．已知函数．

(1)求函数的定义域，井判断函数的奇偶性；

(2)解关于x的不等式．

【答案】(1)，奇函数

(2)

【分析】（1）根据对数函数的性质可求得定义域；根据函数奇偶性的定义可判断函数的奇偶性；

（2）将化为，再利用函数的单调性得到，解不等式结合函数的定义域可得答案.

【详解】(1)由，得函数的定义域为，定义域关于原点对称，

又,

所以函数奇函数；

(2)因为，

所以不等式可化为，

因为在是增函数，所以有，

又，所以，解得，又，

因此不等式的解集为．

18．已知正整数n满足.

(1)求n；

(2)求的展开式中的系数.（用数字表示结果）

【答案】(1)

(2)330

【分析】（1）利用组合数公式及排列数公式得到方程，解得即可；

（2）依题意可得展开式中的系数为，再根据组合数的性质计算可得；

【详解】(1)解：因为，

所以，

即，

解得或（舍去）.

(2)解：由（1）可得，所以展开式中的系数为

.

所以展开式中的系数为330.

19．二项式的展开式中，求：

（1）二项式系数之和；

（2）各项系数之和；

（3）所有奇数项系数之和.

【答案】（1）；（2）；（3）.

【解析】（1）根据二项式系数的性质即可求解；

（2）设,令，代入即可求解；

（3）由（2），再令，两式相加即可求解.

【详解】设.

（1）二项式系数之和为.

（2）各项系数之和为，

令，得.

（3）由（2）知，①

令，

得，②

将①②两式相加，得，

此即为所有奇数项系数之和.

20．1933年7月11日，中华苏维埃共和国临时中央政府根据中央革命军事委员会6月30日的建议，决定8月1日为中国工农红军成立纪念日，中华人民共和国成立后，将此纪念日改称为中国人民解放军建军节，为庆祝建军节，某校举行“强国强军”知识竞赛，该校某班经过层层筛选，还有最后一个参赛名额要在，两名学生中间产生，该班委设计了一个测试方案：，两名学生各自从6个问题中随机抽取3个问题作答，已知这6个问题中，学生能正确回答其中的4个问题，而学生能正确回答每个问题的概率均为，，两名学生对每个问题回答正确与否都是相互独立、互不影响的．

（1）求恰好答对两个问题的概率；

（2）设答对题数为，答对题数为，若让你投票决定参赛选手，你会选择哪名学生？请说明理由．

【答案】（1）；（2）选择投票给学生；理由见解析．

【分析】（1）根据古典概型运算公式进行求解即可；

（2）根据古典概型运算公式求出随机变量的数学期望和方差，结合二项分布的定义求出随机的数学期望和方差，最后利用数学期望和方差的性质进行判断即可.

【详解】解析：（1）恰好答对两个问题的概率为：；

（2）所有可能的取值为1，2，3．

；；．

所以．

由题意，随机变量，所以．

，．

因为，，

可见，与的平均水平相当，但比的成绩更稳定，

所以选择投票给学生．

21．如图，某市有南、北两条城市主干道，在出行高峰期，北干道有，，，，四个交通易堵塞路段，它们被堵塞的概率都是，南干道有，，两个交通易堵塞路段，它们被堵塞的概率分别为，．某人在高峰期驾车从城西开往城东，假设以上各路段是否被堵塞互不影响．

(1)求北干道的，，，个易堵塞路段至少有一个被堵塞的概率；

(2)若南干道被堵塞路段的个数为，求的分布列及数学期望；

(3)若按照“平均被堵塞路段少的路线是较好的高峰期出行路线”的标准，则从城西开往城东较好的高峰期出行路线是哪一条？请说明理由．

【答案】(1)

(2)分布列见解析，

(3)高峰期选择南干道路线较好，理由见解析

【分析】（1）正难则反，先求出四个路段全通勤的概率，用1减去即可求解；

（2）确定，结合独立事件概率公式写出分布列，即可求解；

（3）设北干道被堵塞路段的个数为，则，求出，比较，大小即可求解.

【详解】(1)记北干道的，，，四个易堵塞路段至少有一个被堵塞为事件A，

则；

(2)由题意可知的可能取值为0，1，2，

，

，

．

随机变量的分布列为：

；

(3)设北干道被堵塞路段的个数为，则，

所以．

因为，所以高峰期选择南干道路线较好．

22．某超市开展购物抽奖送积分活动，每位顾客可以参加（，且）次抽奖，每次中奖的概率为，不中奖的概率为，且各次抽奖相互独立．规定第1次抽奖时，若中奖则得10分，否则得5分．第2次抽奖，从以下两个方案中任选一个；

方案① ：若中奖则得30分，否则得0分；

方案② ：若中奖则获得上一次抽奖得分的两倍，否则得5分．

第3次开始执行第2次抽奖所选方案，直到抽奖结束．

(1)如果，以抽奖的累计积分的期望值为决策依据，顾客甲应该选择哪一个方案？并说明理由；

(2)记顾客甲第i次获得的分数为，并且选择方案②．请直接写出与的递推关系式，并求的值．（精确到0.1，参考数据：．）

【答案】(1)应选择方案① ，理由见解析；

(2)，

【分析】（1）分别求得两个方案的累计积分的期望值即可进行选择；

（2）依据题给条件即可求得的值．

【详解】(1)若甲第2次抽奖选方案①，两次抽奖累计积分为，则的可能取值为40，35，10，5．       

，，

，，

所以．            

若甲第2次抽奖选方案②，两次抽奖累计积分为，则的可能取值为30，15，10，

则，，，，       

因为，所以应选择方案①．

(2)依题意得，          

的可能取值为10，5其分布列为

所以，则，       

由得，        

所以为等比数列．其中首项为，公比为．        

所以，故．