

2022届中考数学冲刺猜题卷 天津专版
展开2022届中考数学冲刺猜题卷
天津专版
【满分:120】
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.算式中的括号内应填( )
A. B. C. D.
2.下图均由正六边形与两条对角线所组成,其中不是轴对称图形的是( )
A. B.
C. D.
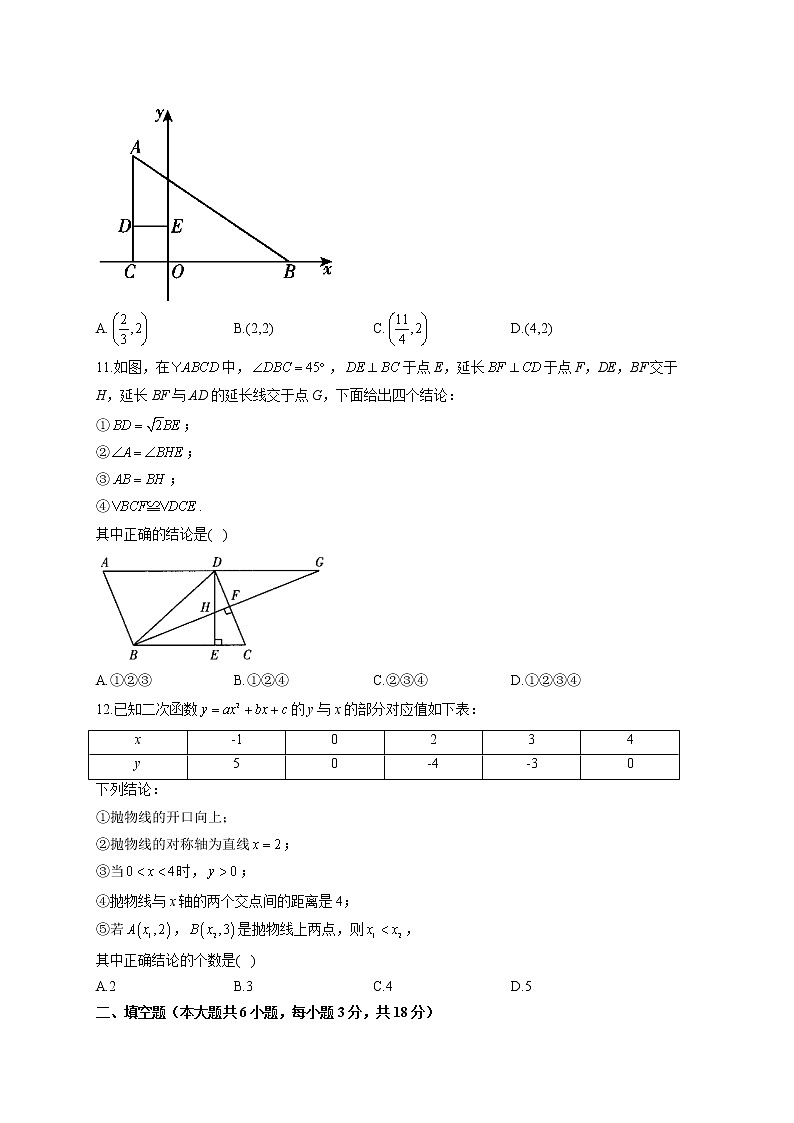
3.国务院总理李克强2020年5月22日在作政府工作报告时说,去年我国农村贫困人口减少11090000,脱贫攻坚取得决定性成就.数据11090000用科学记数法表示为( )
A. B. C. D.
4.由6个大小相同的正方体搭成的几何体如图所示,比较它的主视图,左视图和俯视图的面积,则从正面看( )
A.三个视图的面积一样大 B.主视图的面积最小
C.左视图的面积最小 D.俯视图的面积最小
5.下列运算正确的是( )
A. B. C. D.
6.如图,在中,,CD为AB边上的中线,延长CB至点E,使,连接DE,取DE中点F,连接BF.若,,则BF的长为( )
A.2 B.2.5 C.3 D.4
7.不等式组的解集在以下数轴表示中正确的是( )
A. B.
C. D.
8.如图,线段AB两个端点的坐标分别为,,以原点O为位似中心,将线段AB缩小为原来的,得到线段CD,则线段AB的中点E的对应点的坐标为( )
A. B. C.或 D.或
9.甲、乙两地相距600 km,提速前动车的速度为v km/h,提速后动车的速度是提速前的1.2倍,提速后行车时间比提速前减少20 min,则可列方程为( )
A. B.
C. D.
10.如图,在中, ,边BC在x轴上,顶点A, B的坐标分别为(-2,6)和(7,0).将正方形OCDE沿x轴向右平移,当点E落在AB边上时,点D的坐标为( )
A. B.(2,2) C. D.(4,2)
11.如图,在中,,于点E,延长于点F,DE,BF交于H,延长BF与AD的延长线交于点G,下面给出四个结论:
①;
②;
③;
④.
其中正确的结论是( )
A.①②③ B.①②④ C.②③④ D.①②③④
12.已知二次函数的y与x的部分对应值如下表:
x | -1 | 0 | 2 | 3 | 4 |
y | 5 | 0 | -4 | -3 | 0 |
下列结论:
①抛物线的开口向上;
②抛物线的对称轴为直线;
③当时,;
④抛物线与x轴的两个交点间的距离是4;
⑤若,是抛物线上两点,则,
其中正确结论的个数是( )
A.2 B.3 C.4 D.5
二、填空题(本大题共6小题,每小题3分,共18分)
13.化简:___________.
14.关于x的一元二次方程有两个不相等的实数根,则m的最小整数值是________.
15.如图,在中,,PQ垂直平分AB,垂足为Q,交BC于点P.按以下步骤作图:①以点A为圆心,以适当的长为半径作弧,分别交边AC,AB于点D,E;②分别以点D,E为圆心,以大于的长为半径作弧,两弧相交于点F;③作射线AF.若AF与PQ的夹角为,则________°.
16.现有两个不透明的袋子,一个装有2个红球、1个白球,另一个装有1个黄球、2个红球,这些球除颜色外完全相同.从两个袋子中各随机摸出1个球,摸出的两个球颜色相同的概率是________.
17.如图,菱形ABCD的对角线长分别为6和8,点O为对角线的交点,过点O折叠菱形,点B,C的对应点分别为点,,MN是折痕.若,则MN的长为__________.
18.如图,点A为函数图象上一点,连接OA,交函数的图象于点B,点C是x轴上一点,且,则的面积为______________.
三、解答题(本大题共7小题,共66分.解答应写出文字说明、演算步骤或推理过程)
19.(8分)对于任意的有理数,我们规定:,根据这一规定,解答以下问题:若同时满足,求的值.
20.(8分)“安全教育平台”是中国教育学会为方便家长和学生参与安全知识活动、接受安全提醒的一种应用软件.某校为了了解家长和学生参与“防溺水教育”的情况,在本校学生中随机抽取部分学生做调查,把收集的数据分为以下4类情形:
A.仅学生自己参与;
B.家长和学生一起参与;
C.仅家长自己参与;
D家长和学生都未参与.
请根据图中提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查了__________名学生;
(2)补全条形统计图,并在扇形统计图中计算C类所对应扇形的圆心角的度数;
(3)根据抽样调查结果,估计该校2000名学生中“家长和学生都未参与”的人数.
21.(10分)随着我市农产品整体品牌形象“聊·胜一筹”的推出,现代农业得到了更快发展.某农场为扩大生产建设了一批新型钢管装配式大棚,如图1.线段分别表示大棚的墙高和跨度,表示保温板的长.已知墙高为2米,墙面与保温板所成的角,在点D处测得A点、C点的仰角分别为9°,15.6°,如图2.求保温板的长约是多少米?(精确到0.1米)
(参考数据:, ,)
22.(10分)如图,在中,AB为的直径,交AC边于点D,连接OD,过点D作的切线DE,且于点E,.
(1)求证:;
(2)若,的直径为5,求.
23.(10分)在初中阶段的函数学习中,我们经历了列表、描点、连线画函数图象,并结合图象研究函数性质的过程.以下是我们研究函数性质及其应用的部分过程,请按要求完成下列各小题.
(1)请把下表补充完整,并在图中补全该函数图象.
x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
… |
| -3 | 0 | 3 |
| … |
(2)根据函数图象,判断下列关于该函数性质的说法是否正确,正确的在相应的括号内打“√”,错误的在相应的括号内打“×”.
①该函数图象是轴对称图形,它的对称轴为y轴.( )
②该函数在自变量的取值范围内,有最大值和最小值.当时,函数取得最大值3;当时,函数取得最小值-3.( )
③当或时,y随x的增大而减小;当时,y随x的增大而增大.( )
(3)已知函数的图象如图所示,结合你所画的函数图象,直接写出不等式的解集(保留1位小数,误差不超过0.2).
24.(10分)如图(1),边长为4的正方形ABCD与边长为a的正方形CFEG的顶点C重合,点E在线段AC上.
(1)问题发现
如图(1)所示,AE与BF的数量关系为______________.
(2)类比探究
如图(2)所示,将正方形CFEG绕点C旋转,旋转角为a(),连接AE,BF,此时(1)中结论是否还成立?若成立,请写出证明过程;若不成立,请说明理由.
(3)拓展延伸
若点F为BC的中点,将正方形CFEG绕点C旋转,当点A,F,G在一条直线上时,线段AG的长度为_____________.
25.(10分)在平面直角坐标系xOy中,已知抛物线经过点,且其顶点坐标为,如图,直线与抛物线交于、B两点,直线l为.
(1)求抛物线的解析式.
(2)在l上是否存在一点P,使取得最小值?若存在,求出点P的坐标;若不存在,请说明理由.
(3)已知为平面内一定点,为抛物线上一动点,且点M到直线l的距离与点M到点F的距离总相等,求定点F的坐标.
答案以及解析
1.答案:D
解析:,故选D.
2.答案:D
解析:D选项中的图形不是轴对称图形,故选D.
3.答案:B
解析:,故选B.
4.答案:C
解析:主视图有5个小正方形,左视图有3个小正方形,俯视图有4个小正方形,因此左视图的面积最小.故选C.
5.答案:C
解析:,故选项A错误;,故选项B错误;,故选项C正确;,故选项D错误.故选C.
6.答案:B
解析:在中,.是斜边上的中线,.,点F为DE的中点,是的中位线,.
7.答案:B
解析:由①得,,由②得,,
所以不等式组的解集是,故选B.
8.答案:C
解析:,,AB的中点E的坐标为.以原点O为位似中心,将线段AB缩小为原来的,点E的对应点的坐标为或,即或.故选C.
9.答案:A
解析:提速前后行车时间分别是,,
因为提速后行车时间比提速前减少20 min,所以,
即,故选A.
10.答案:B
解析:设直线AB的解析式为,把A(-2,6)和B(7,0)分别代入,得解得故直线AB的解析式为.,四边形OCDE为正方形,正方形的边长为2,点D,E的纵坐标均为2.把代入,得,解得,当点E落在AB边上时,其坐标为(4,2),此时点D的坐标为(2,2),故选B.
11.答案:A
解析:,,在中,,,,故①正确;,,,,,又在中,,,故②正确;在和中,,,,四边形ABCD为平行四边形,,,故③正确;利用已知条件不能得到,故④错误.故选A.
12.答案:B
解析:设抛物线的表达式为,把代入得,解得,抛物线的表达式为,所以①正确;
抛物线的对称轴为直线,所以②正确;
抛物线与x轴的交点坐标为,,当时,,所以③错误;
抛物线与x轴的两个交点间的距离是4,所以④正确;
若,是抛物线上两点,则或,所以⑤错误.故选B.
13.答案:
解析:.
14.答案:0
解析:一元二次方程有两个不相等的实数根,
,
;
故答案为0.
15.答案:55
解析:设AF与QP相交于点M.
在中,,,
所以,
由作图易知AF是的平分线,
所以,
因为PQ是AB的垂直平分线,所以,
所以,所以.
16.答案:
解析:列表如下:
| 黄 | 红 | 红 |
红 | (红,黄) | (红,红) | (红,红) |
红 | (红,黄) | (红,红) | (红,红) |
白 | (白,黄) | (白,红) | (白,红) |
由表可知共有9种等可能的结果,其中摸出的两个球颜色相同的结果有4种,所以摸出的两个球颜色相同的概率为.
17.答案:
解析:如图,延长交DC的延长线于点E.四边形ABCD是菱形,.易得,.,,,,.由折叠的性质可知,.
18.答案:6
解析:设点A的坐标为,
点B的坐标为.
点C是x轴上一点,且,
点C的坐标是.
设过点,的直线的解析式为,
,解得.的解析式为.
又点在上,,
解得或(舍去),
.
19.答案:
解析:根据题意可知解得
当时,
.
20.答案:(1)400
(2)54°
(3)100
解析:(1)(名).
所以共调查了400名学生.
(2)如图.
C类所对应扇形的圆心角的度数为.
(3)(名).
答:估计该校2000名学生中“家长和学生都未参与”的人数为100.
21.答案:1.5
解析:设米,在中,米,
如图,作,垂足为E,作,垂足为G,
在中,,
,
(米),
(米),
米.
在中,,
(米),
又米,
,
即,
解方程,得.
答:保温板的长约是1.5米.
22.答案:(1)见解析
(2)
解析:(1)为的切线,.
,,.,,,.
(2)如图,连接BD,设,.
为直径,.
,,,,,
在中,,即,解得,(舍去),
,即.
23.答案:解:(1)补充表格如下,补全的函数图象如图所示.
x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
… |
|
| -1.8 |
|
|
|
|
| 1.8 |
|
| … |
(2)①×,②√,③√.
(3)或.
24.答案:(1).
(2)(1)中结论还成立.
证明:连接CE.
,
.
在和中,,,
,
,
(3)或
解法提示:分两种情况讨论.
①当点F在AG上时,如图(1),过点C作于点H,则.
在中,由勾股定理可得.
故.
②当点F在AG的延长线上时,如图(2),过点C作于点H,则.
在中,由勾股定理可得,
.
综上可知,AG的长为或.
25.答案:解:(1)抛物线的顶点坐标为,
设抛物线的解析式为.
该抛物线经过点,,解得,
抛物线的解析式为.
(2)存在.
作点B关于直线l的对称点,连接交直线l于点P,此时,取得最小值(如图所示).
点,直线l为,点的坐标为.
设直线的解析式为,
将、分别代入,得解得
直线的解析式为,
当时,,解得,
点P的坐标为.
(3)点M到直线l的距离与点M到点F的距离总相等,
,
.
为抛物线上一动点,
,
,
整理得.
m为任意值,
定点F的坐标为.
2022届中考数学冲刺猜题卷 吉林长春专版: 这是一份2022届中考数学冲刺猜题卷 吉林长春专版,共18页。
2022届中考数学冲刺猜题卷 山东菏泽专版: 这是一份2022届中考数学冲刺猜题卷 山东菏泽专版,共19页。
2022届中考数学冲刺猜题卷 山东烟台专版: 这是一份2022届中考数学冲刺猜题卷 山东烟台专版,共18页。












