安徽省九年级2022中考数学冲刺复习-25解答题压轴必刷45题①

这是一份安徽省九年级2022中考数学冲刺复习-25解答题压轴必刷45题①，共23页。试卷主要包含了为完美点，阅读材料并回答下列问题等内容，欢迎下载使用。

25解答题压轴必刷45题①

一．一元一次方程的应用（共3小题）
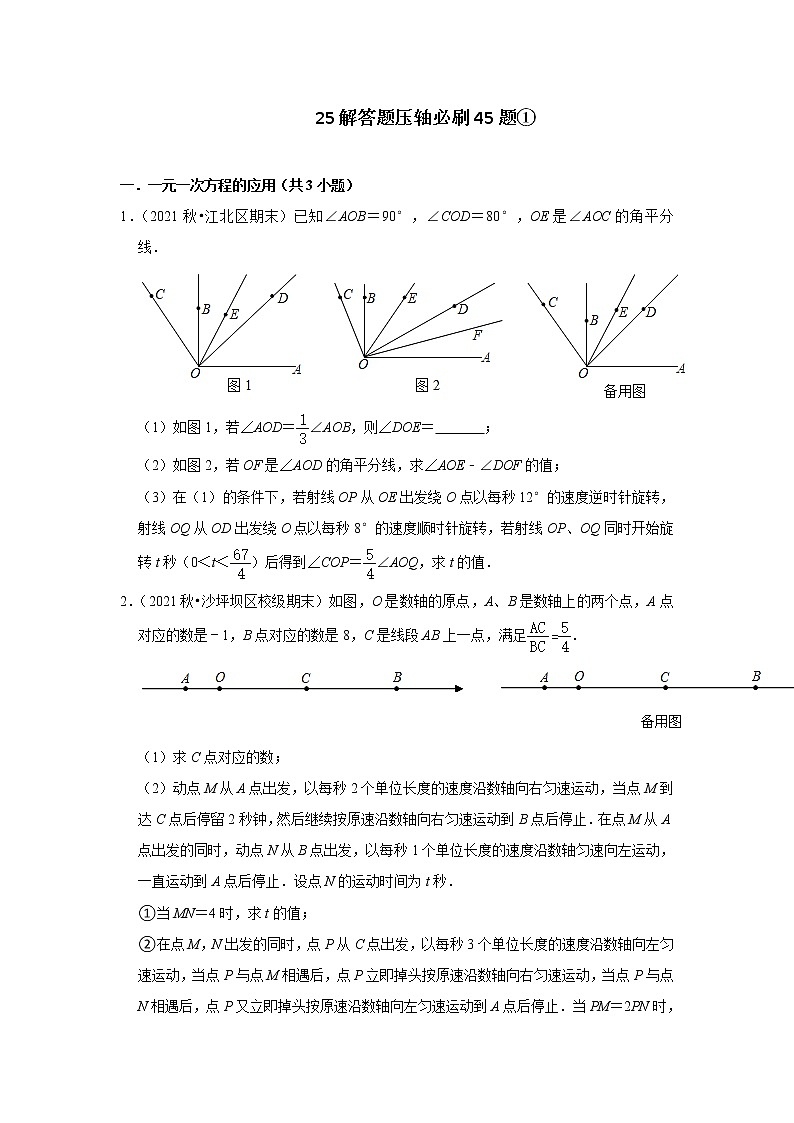
1．（2021秋•江北区期末）已知∠AOB＝90°，∠COD＝80°，OE是∠AOC的角平分线．

（1）如图1，若∠AOD＝∠AOB，则∠DOE＝　 　；
（2）如图2，若OF是∠AOD的角平分线，求∠AOE﹣∠DOF的值；
（3）在（1）的条件下，若射线OP从OE出发绕O点以每秒12°的速度逆时针旋转，射线OQ从OD出发绕O点以每秒8°的速度顺时针旋转，若射线OP、OQ同时开始旋转t秒（0＜t＜）后得到∠COP＝∠AOQ，求t的值．
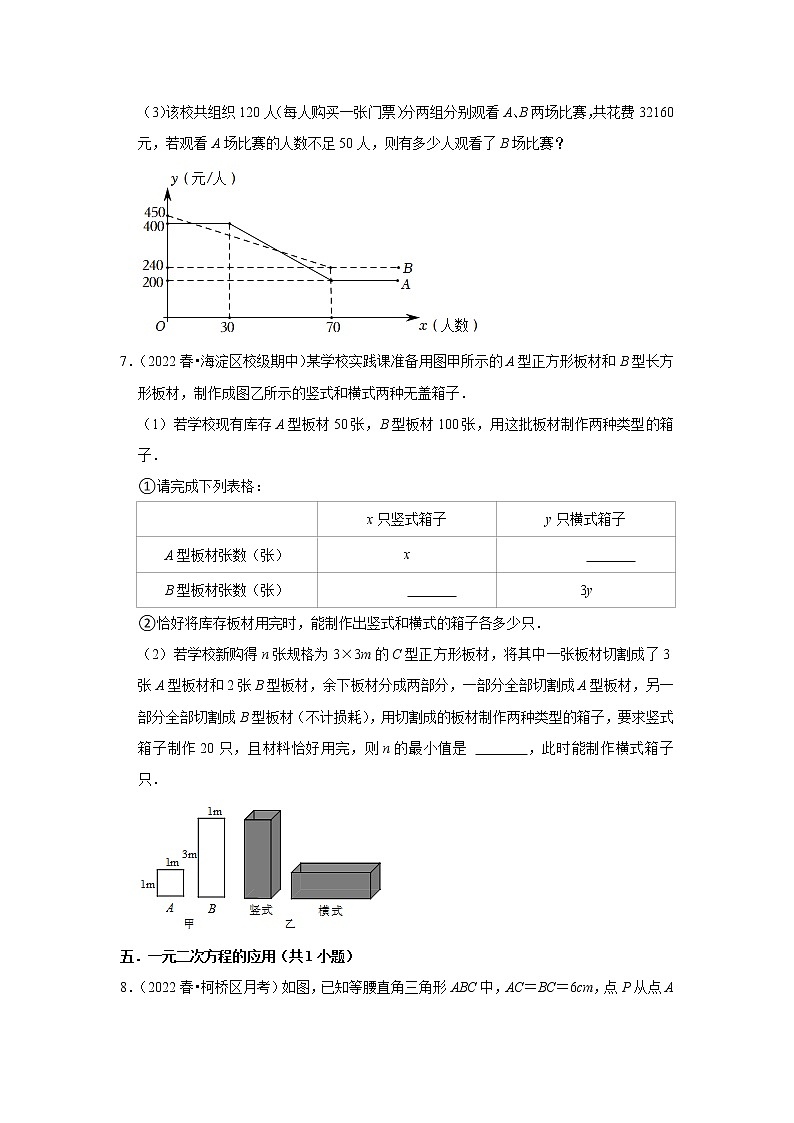
2．（2021秋•沙坪坝区校级期末）如图，O是数轴的原点，A、B是数轴上的两个点，A点对应的数是﹣1，B点对应的数是8，C是线段AB上一点，满足．

（1）求C点对应的数；
（2）动点M从A点出发，以每秒2个单位长度的速度沿数轴向右匀速运动，当点M到达C点后停留2秒钟，然后继续按原速沿数轴向右匀速运动到B点后停止．在点M从A点出发的同时，动点N从B点出发，以每秒1个单位长度的速度沿数轴匀速向左运动，一直运动到A点后停止．设点N的运动时间为t秒．
①当MN＝4时，求t的值；
②在点M，N出发的同时，点P从C点出发，以每秒3个单位长度的速度沿数轴向左匀速运动，当点P与点M相遇后，点P立即掉头按原速沿数轴向右匀速运动，当点P与点N相遇后，点P又立即掉头按原速沿数轴向左匀速运动到A点后停止．当PM＝2PN时，请直接写出t的值．
3．（2021秋•槐荫区期末）某工人计划加工一批产品，如果每小时加工产品10个，就可以在预定时间完成任务，如果每小时多加工2个，就可以提前1小时完成任务．
（1）该产品的预定加工时间为几小时？
（2）若该产品销售时的标价为100元/个，按标价的八折销售时，每个仍可以盈利25元，该批产品总成本为多少元？
二．二元一次方程组的解（共1小题）
4．（2018春•龙岩期末）当a，b都是实数，且满足2a﹣b＝6，就称点P（a﹣1，+1）为完美点．
（1）判断点A（2，3）是否为完美点．
（2）已知关于x，y的方程组，当m为何值时，以方程组的解为坐标的点B（x，y）是完美点，请说明理由．
三．解二元一次方程组（共1小题）
5．（2021春•金乡县期末）阅读材料并回答下列问题：
当m，n都是实数，且满足2m＝8+n，就称点P（m﹣1，）为“爱心点”．
（1）判断点A（5，3），B（4，6）哪个点为“爱心点”，并说明理由；
（2）若点C（a，﹣8）也是“爱心点”，请求出a的值；
（3）已知p，q为有理数，且关于x，y的方程组解为坐标的点B（x，y）是“爱心点”，求p，q的值．
四．二元一次方程组的应用（共2小题）
6．（2022•泗阳县一模）2022年2月4日，第24届冬季奥林匹克运动会在北京胜利召开，在冬奥会期间，北京某校打算组织部分师生利用周日时间到现场观看比赛，经了解在离学校最近的比赛场馆当日共有A、B两场比赛，两场比赛的票价如下图所示，其中x轴表示一次性购票人数，y轴表示每张票的价格，如：一次性购买A场比赛门票10张，票价为400元/张，若一次性购买A场比赛门票80张，则每张票价为200元．
（1）若一次性购买B场比赛门票10张，则每张票价为 　 　元（直接写出结果）．
（2）若一次性购买A场比赛门票a（50＜a＜60）张，需支付门票费用多少元？（用a的代数式表示）
（3）该校共组织120人（每人购买一张门票）分两组分别观看A、B两场比赛，共花费32160元，若观看A场比赛的人数不足50人，则有多少人观看了B场比赛？

7．（2022春•海淀区校级期中）某学校实践课准备用图甲所示的A型正方形板材和B型长方形板材，制作成图乙所示的竖式和横式两种无盖箱子．
（1）若学校现有库存A型板材50张，B型板材100张，用这批板材制作两种类型的箱子．
①请完成下列表格：

x只竖式箱子
y只横式箱子
A型板材张数（张）
x
　 　
B型板材张数（张）
　 　
3y
②恰好将库存板材用完时，能制作出竖式和横式的箱子各多少只．
（2）若学校新购得n张规格为3×3m的C型正方形板材，将其中一张板材切割成了3张A型板材和2张B型板材，余下板材分成两部分，一部分全部切割成A型板材，另一部分全部切割成B型板材（不计损耗），用切割成的板材制作两种类型的箱子，要求竖式箱子制作20只，且材料恰好用完，则n的最小值是 　 　，此时能制作横式箱子 　 　只．

五．一元二次方程的应用（共1小题）
8．（2022春•柯桥区月考）如图，已知等腰直角三角形ABC中，AC＝BC＝6cm，点P从点A出发，沿A→C→B的方向以2cm/s的速度向终点B运动，同时点Q从点B出发，沿B→A的方向以cm/s的速度向终点A运动．当点P运动到点B时，两点均停止运动．运动时间记为t秒，请解决下列问题：
（1）若点P在边AC上，当t为何值时，△APQ为直角三角形？
（2）是否存在这样的t值，使△APQ的面积为8cm2？若存在，请求出t的值，若不存在，请说明理由．


六．分式方程的应用（共3小题）
9．（2022•市中区校级模拟）在汕头市“创文”活动中，一项绿化工程由甲、乙两工程队承担．已知甲工程队单独完成这项工作需120天，甲工程队单独工作30天后，乙工程队参与合做，两队又共同工作了36天完成．
（1）求乙工程队单独完成这项工作需要多少天？
（2）因工期的需要，将此项工程分成两部分，甲做其中一部分用了a天完成，乙做另一部分用了y天完成．若乙工程队还有其它工作任务，最多只能做52天．求甲工程队至少应做多少天？
10．（2021秋•上思县期末）为改善南宁市的交通现状，市政府决定修建地铁，甲、乙两工程队承包地铁1号线的某段修建工作，从投标书中得知：甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的3倍；若由甲队先做20天，剩下的工程再由甲、乙两队合作10天完成．
（1）求甲、乙两队单独完成这项工程各需多少天？
（2）已知甲队每天的施工费用为15.6万元，乙队每天的施工费用为18.4万元，工程预算的施工费用为500万元，为缩短工期，拟安排甲、乙两队同时开工合作完成这项工程，那么工程预算的施工费用是否够用？若不够用，需增加多少万元？
11．（2022春•浦东新区校级期中）某汽车装配厂计划在规定的时限内组装汽车21辆，组装了6辆汽车后，又追加了组装5辆汽车的订单，要求交货时间不超过原来规定的期限，通过挖潜改革，提高工效，平均每天比原计划多组装2辆汽车，结果提前1天交货．问追加订单后，平均每天组装多少辆汽车？
七．一元一次不等式的应用（共3小题）
12．（2022•德城区模拟）某商场用60个A型包装袋与90个B型包装袋对甲，乙两类农产品进行包装出售（两种型号包装袋都用完），每个A型包装袋装2千克甲类农产品或装3千克乙类农产品，每个B型包装袋装3千克甲类农产品或装5千克乙类农产品，设有x个A型包装袋包装甲类农产品，有y个B型包装袋包装甲类农产品．
（1）请用含x或y的代数式填空完成表：
包装袋型号
A
B
甲类农产品质量（千克）
2x
　 　
乙类农产品质量（千克）
　 　
5（90﹣y）
（2）若甲、乙两类农产品的总质量分别是260千克与210千克，求x，y的值．
（3）若用于包装甲类农产品的B型包装袋数量是用于包装甲类农产品的A型包装袋数量的两倍，且它们数量之和不少于90个，记甲、乙两类农产品的总质量之和为m千克，求m的最小值与最大值．
13．（2022春•恩阳区 期中）某商店取厂家选购甲、乙两种商品，乙商品每件进价比甲商品每件进价多20元，若购进甲商品5件和乙商品4件共需要800元；
（1）求甲、乙两种商品每件的进价分别是多少元？
（2）若甲种商品的售价为每件100元，乙种商品的售价为每件125元，该商店准备购进甲、乙两种商品共40件，且这两种商品全部售出后总利润不少于900元，则甲种商品最多可购进多少件？
14．（2018•葫芦岛）某爱心企业在政府的支持下投入资金，准备修建一批室外简易的足球场和篮球场，供市民免费使用，修建1个足球场和1个篮球场共需8.5万元，修建2个足球场和4个篮球场共需27万元．
（1）求修建一个足球场和一个篮球场各需多少万元？
（2）该企业预计修建这样的足球场和篮球场共20个，投入资金不超过90万元，求至少可以修建多少个足球场？
八．一元一次不等式组的整数解（共1小题）
15．（2022春•吉安月考）对m、n定义一种新运算“※”，规定：m※n＝am﹣bn+5（a．b均为非零常数），等式右边的运算是通常的四则运算，例如3※4＝3a﹣4b+5．已知2※3＝1，3※（﹣1）＝10．
（1）求a、b的值；
（2）若关于x的不等式组有且只有一个整数解，试求字母t的取值范围．





【参考答案】
一．一元一次方程的应用（共3小题）
1．（2021秋•江北区期末）已知∠AOB＝90°，∠COD＝80°，OE是∠AOC的角平分线．

（1）如图1，若∠AOD＝∠AOB，则∠DOE＝　25°　；
（2）如图2，若OF是∠AOD的角平分线，求∠AOE﹣∠DOF的值；
（3）在（1）的条件下，若射线OP从OE出发绕O点以每秒12°的速度逆时针旋转，射线OQ从OD出发绕O点以每秒8°的速度顺时针旋转，若射线OP、OQ同时开始旋转t秒（0＜t＜）后得到∠COP＝∠AOQ，求t的值．
【解析】解：（1）∵∠AOB＝90°，
∴∠AOD＝∠AOB＝30°，
∵∠COD＝80°，
∴∠AOC＝∠AOD+∠COD＝30°+80°＝110°，
∵OE平分∠AOC，
∴∠AOE＝∠COE＝∠AOC＝55°，
∴∠DOE＝∠AOE﹣∠AOD＝55°﹣30°＝25°；
故答案为：25°；
（2）∵OF平分∠AOD，
∴∠AOF＝∠DOF＝∠AOD，
∵OE平分∠AOC，
∴∠AOE＝∠AOC，
∴∠AOE﹣∠AOF＝∠AOC﹣∠AOD＝（∠AOC﹣∠AOD）＝∠COD，
又∵∠COD＝80°，
∴∠AOE﹣∠DOF＝×80°＝40°；
（3）分三种情况：
①当射线OP、OQ在∠AOC内部时，
∵30﹣8t≥0，
∴t≤3.75，
即0＜t≤3.75时，
由题意得：∠POE＝（12t）°，∠DOQ＝（8t）°，
∴∠COP＝∠COE﹣∠POE＝（55﹣12t）°，∠AOQ＝∠AOD﹣∠DOQ＝（30﹣8t）°，
∵∠COP＝∠AOQ，
∴55﹣12t＝（30﹣8t），
解得：t＝（舍去）；
②当射线OP在∠AOC内部时，射线OQ在∠AOC外部时，
∵55﹣12t≥0，
∴t≤4.5，
即3.75＜t≤4.5时，
则∠COP＝∠COE﹣∠POE＝（55﹣12t）°，∠AOQ＝∠DOQ﹣∠AOD＝（8t﹣30）°，
∴55﹣12t＝（8t﹣30），
解得：t＝；
③当射线OP、OQ在∠AOC外部时，
∵0＜t＜，
∴＝16.75，
即4.5＜t＜16.75时，
则∠COP＝∠POE﹣∠COE＝（12t﹣55）°，∠AOQ＝∠DOQ﹣∠AOD＝（8t﹣30）°，
∴12t﹣55＝（8t﹣30），
解得：t＝；
综上所述，t的值为秒或秒．
2．（2021秋•沙坪坝区校级期末）如图，O是数轴的原点，A、B是数轴上的两个点，A点对应的数是﹣1，B点对应的数是8，C是线段AB上一点，满足．

（1）求C点对应的数；
（2）动点M从A点出发，以每秒2个单位长度的速度沿数轴向右匀速运动，当点M到达C点后停留2秒钟，然后继续按原速沿数轴向右匀速运动到B点后停止．在点M从A点出发的同时，动点N从B点出发，以每秒1个单位长度的速度沿数轴匀速向左运动，一直运动到A点后停止．设点N的运动时间为t秒．
①当MN＝4时，求t的值；
②在点M，N出发的同时，点P从C点出发，以每秒3个单位长度的速度沿数轴向左匀速运动，当点P与点M相遇后，点P立即掉头按原速沿数轴向右匀速运动，当点P与点N相遇后，点P又立即掉头按原速沿数轴向左匀速运动到A点后停止．当PM＝2PN时，请直接写出t的值．
【解析】解：（1）∵A点对应的数是﹣1，B点对应的数是8，
∴AB＝9，
∵＝，
∴AC＝5，BC＝4，
∴C点对应的数是8﹣BC＝8﹣4＝4，
答：C点对应的数是4；
（2）①设运动t秒时，MN＝4
当M、N未相遇，则M在AC上运动，M表示的数是﹣1+2t，N在BC上运动，N表示的数是8﹣t，
∴8﹣t﹣（﹣1+2t）＝4，
解得t＝，
当M、N相遇后，M在BC上运动，M表示的数是4+2（t﹣﹣2）＝2t﹣5，N在AC上运动，N表示的数是8﹣t，
∴2t﹣5﹣（8﹣t）＝4，
解得t＝，
综上所述，t的值为或；
②P与M还未第一次相遇时，P表示的数是4﹣3t，M表示的数是﹣1+2t，N表示的数是8﹣t，
∴4﹣3t﹣（﹣1+2t）＝2[8﹣t﹣（4﹣3t）]，
解得t＝﹣（舍去），此种情况不存在，
由已知得，P与M在t＝1时第一次相遇，相遇后P掉头按原速沿数轴向右匀速运动，在未遇到N前，P表示的数是（4﹣3×1）+3（t﹣1）＝3t﹣2，
∴3t﹣2﹣（﹣1+2t）＝2[8﹣t﹣（3t﹣2）]，
解得t＝，
由已知可知，当P与M在表示1的点处相遇，此时N运动到表示7的点处，再经过＝1.5秒，即t＝2.5时，P与N相遇，此时M正好运动到C，P与N相遇后
又立即掉头按原速沿数轴向左匀速运动，未与M第二次相遇，此时P表示的数是（8﹣2.5）﹣3（t﹣2.5）＝13﹣3t，
∴13﹣3t﹣4＝2[8﹣t﹣（13﹣3t）]，
解得t＝，
当P与M第二次相遇后，P表示的数是13﹣3t，M在BC上运动，M表示的数是2t﹣5，
∴2t﹣5﹣（13﹣3t）＝2[8﹣t﹣（13﹣3t）]，
解得t＝8，此时13﹣3t＝﹣11＜﹣1，
∴t＝8舍去，这种情况不存在，
综上所述，t的值为或．
3．（2021秋•槐荫区期末）某工人计划加工一批产品，如果每小时加工产品10个，就可以在预定时间完成任务，如果每小时多加工2个，就可以提前1小时完成任务．
（1）该产品的预定加工时间为几小时？
（2）若该产品销售时的标价为100元/个，按标价的八折销售时，每个仍可以盈利25元，该批产品总成本为多少元？
【解析】解：（1）设这批产品需要加工x个，
＝1，
x＝60，
60÷10＝6，
答：该产品的预定加工时间为6小时；
（2）设该批产品成本为a元/个，
100×80%＝a+25，
a＝55，
55×60＝3300，
答：该批产品总成本为3300元．
二．二元一次方程组的解（共1小题）
4．（2018春•龙岩期末）当a，b都是实数，且满足2a﹣b＝6，就称点P（a﹣1，+1）为完美点．
（1）判断点A（2，3）是否为完美点．
（2）已知关于x，y的方程组，当m为何值时，以方程组的解为坐标的点B（x，y）是完美点，请说明理由．
【解析】解：（1）a﹣1＝2，可得a＝3，+1＝3，可得b＝4，
∵2a﹣b≠6，
∴A（2，3）不是完美点．

（2）∵，
∴，
3+m＝a﹣1，可得a＝m+4，
3﹣m＝+1，可得b＝4﹣2m，
∵2a﹣b＝6，
∴2m+8﹣4+2m＝6，
∴m＝，
∴当m＝时，点B（x，y）是完美点．
三．解二元一次方程组（共1小题）
5．（2021春•金乡县期末）阅读材料并回答下列问题：
当m，n都是实数，且满足2m＝8+n，就称点P（m﹣1，）为“爱心点”．
（1）判断点A（5，3），B（4，6）哪个点为“爱心点”，并说明理由；
（2）若点C（a，﹣8）也是“爱心点”，请求出a的值；
（3）已知p，q为有理数，且关于x，y的方程组解为坐标的点B（x，y）是“爱心点”，求p，q的值．
【解析】解：（1）点A是爱心点，点B不是爱心点，理由如下：
∵，
∴，
∵2×6＝8+4，
∴点A是爱心点；
∵，
∴，
∵2×5≠8+10，
∴点B不是爱心点；
（2）∵点C为爱心点，
∴，
∴n＝﹣18，
又∵2m＝8+n，
∴2m＝8+（﹣18），
解得m＝﹣5，
∴﹣5﹣1＝a，即a＝﹣6；
（3）解方程组得 ，
又∵点B是爱心点满足：，
∴，
∵2m＝8+n，
∴2 p﹣2q+2＝8+4q﹣2，
整理得：2 p﹣6q＝4，
∵p，q是有理数，
∴p＝0，﹣6q＝4，
∴p＝0，q＝﹣．
四．二元一次方程组的应用（共2小题）
6．（2022•泗阳县一模）2022年2月4日，第24届冬季奥林匹克运动会在北京胜利召开，在冬奥会期间，北京某校打算组织部分师生利用周日时间到现场观看比赛，经了解在离学校最近的比赛场馆当日共有A、B两场比赛，两场比赛的票价如下图所示，其中x轴表示一次性购票人数，y轴表示每张票的价格，如：一次性购买A场比赛门票10张，票价为400元/张，若一次性购买A场比赛门票80张，则每张票价为200元．
（1）若一次性购买B场比赛门票10张，则每张票价为 　420　元（直接写出结果）．
（2）若一次性购买A场比赛门票a（50＜a＜60）张，需支付门票费用多少元？（用a的代数式表示）
（3）该校共组织120人（每人购买一张门票）分两组分别观看A、B两场比赛，共花费32160元，若观看A场比赛的人数不足50人，则有多少人观看了B场比赛？

【解析】解：（1）当x≤70时，设一次性购买B场门票x张，每张票价为y元，
设解析式为y＝kx+b，
将点（0，450）和（70，240）代入，
得，
解得，
∴y＝﹣3x+450，
当x＝10时，y＝﹣30+450＝420．
故答案为：420．
（2）当一次性购买A场比赛门票a（50＜a＜60）张，设每张票价为y元，
设y＝ka+b，
将点（30，400），（70，200）代入，
得，
解得，
∴y＝﹣5a+550，
∴一次性购买A场比赛门票a（50＜a＜60）张，需支付门票费用为：﹣5a2+550a．
（3）设有m人观看了B场比赛，
∵观看A场比赛的人数不足50人，总共有120人，
∴观看B场比赛的人数大于70人，
∴观看B场比赛的每张票240元．
①当观看A场比赛的人数小于等于30的时候，每张票400元，
∴240m+400（120﹣m）＝32160，
解得m＝99．
②当观看A场比赛的人数大于30小于50的时候，每张票（﹣5x+550）元，
∴240m+（120﹣m）（﹣5（120﹣m）+550）＝32160，
解得m＝72或m＝111（舍去），
综上，有99人或72人观看了比赛．
7．（2022春•海淀区校级期中）某学校实践课准备用图甲所示的A型正方形板材和B型长方形板材，制作成图乙所示的竖式和横式两种无盖箱子．
（1）若学校现有库存A型板材50张，B型板材100张，用这批板材制作两种类型的箱子．
①请完成下列表格：

x只竖式箱子
y只横式箱子
A型板材张数（张）
x
　2y　
B型板材张数（张）
　4x　
3y
②恰好将库存板材用完时，能制作出竖式和横式的箱子各多少只．
（2）若学校新购得n张规格为3×3m的C型正方形板材，将其中一张板材切割成了3张A型板材和2张B型板材，余下板材分成两部分，一部分全部切割成A型板材，另一部分全部切割成B型板材（不计损耗），用切割成的板材制作两种类型的箱子，要求竖式箱子制作20只，且材料恰好用完，则n的最小值是 　35　，此时能制作横式箱子 　5　只．

【解析】解：（1）①如图所示：做一个竖式箱子，需1张A板，4张B板，做一个横式箱子，需2张A板，3张B板，
故答案为：4x，2y；
②∵恰好将库存板材用完，根据题意，得
，
解得，
答：制作出竖式和横式的箱子各20只和10只；
（2）设C型板有x张全部切成A板，则有（n﹣x﹣1）张全部切成B板，
且一张3×3m的C型板可以切成3×3＝9张A型板或3张B型板，
得（3+9x）张A板，[2+3（n﹣x﹣1）]＝（3n﹣3x﹣1）张B板，
因为竖式箱子制作20只用掉20张A板，80张B板，
则剩余A板（9x﹣17）张，B板（3n﹣3x﹣81）张，
根据题意，得＝，
整理，得n＝x+，
∵9x﹣17≥0，
∴x≥，
∵3n﹣3x﹣81≥0，
∴n≥x+27，
，
解得，
∵x≥，且x为整数，
∴x取最小值为2时，代入n＝x+，得n＝11+（不符合题意，舍去），
当x＝3时，代入n＝x+，得n＝35，
∴x取最小值为3时，n＝35最小．
此时，剩余A板10张，可以做5只横式板．
∴n的最小值是35，此时能制作横式箱子5只．
故答案为：35，5．
五．一元二次方程的应用（共1小题）
8．（2022春•柯桥区月考）如图，已知等腰直角三角形ABC中，AC＝BC＝6cm，点P从点A出发，沿A→C→B的方向以2cm/s的速度向终点B运动，同时点Q从点B出发，沿B→A的方向以cm/s的速度向终点A运动．当点P运动到点B时，两点均停止运动．运动时间记为t秒，请解决下列问题：
（1）若点P在边AC上，当t为何值时，△APQ为直角三角形？
（2）是否存在这样的t值，使△APQ的面积为8cm2？若存在，请求出t的值，若不存在，请说明理由．


【解析】解：在等腰直角△ABC中，
∵AC＝BC＝6cm，
∴AB＝cm，
（1）设经过t秒，△APQ是直角三角形，此时AP＝2t，AQ＝．
①当∠APQ＝90°时，AQ＝AP，如下图所示：

∴＝，
解得t＝2．
②当∠AQP＝90°时，AP＝AQ，如下图所示：

∴2t＝（ ），
解得t＝3．
∴若P在AC边上，当t＝2或t＝3时△APQ是直角三角形．
（2）①当P在AC边上，连接PQ，过点P作PH⊥AB于H，如下图所示：

设经过t秒，△APQ的面积为为8cm2，
此时AP＝2t，AQ＝．
∴PH＝，
∴÷2＝8，
解得t＝2或t＝4（舍去），
②当点P在BC边上时，连接AP，PQ，作PH⊥AQ于H，如下图所示：

设经过t秒，△APQ的面积为为8cm2，
此时PB＝12﹣2t，AQ＝．
∴PH＝，
∴＝＝8，
解得t＝，或t＝（舍去），
∴当t＝2或t＝时，△APQ的面积为为8cm2．
六．分式方程的应用（共3小题）
9．（2022•市中区校级模拟）在汕头市“创文”活动中，一项绿化工程由甲、乙两工程队承担．已知甲工程队单独完成这项工作需120天，甲工程队单独工作30天后，乙工程队参与合做，两队又共同工作了36天完成．
（1）求乙工程队单独完成这项工作需要多少天？
（2）因工期的需要，将此项工程分成两部分，甲做其中一部分用了a天完成，乙做另一部分用了y天完成．若乙工程队还有其它工作任务，最多只能做52天．求甲工程队至少应做多少天？
【解析】解：（1）设乙工程队单独完成这项工作需要x天，
由题意得：+（+）×36＝1，
解得：x＝80，
经检验x＝80是原方程的解．
答：乙工程队单独做需要80天完成．

（2）因为甲工程队做其中一部分用了a天，乙工程队做另一部分用了y天，
依题意得：+＝1，解得：
y＝80﹣a，
∵y≤52，
∴80﹣a≤52，
解得：a≥42，
答：甲工程队至少应做42天．
10．（2021秋•上思县期末）为改善南宁市的交通现状，市政府决定修建地铁，甲、乙两工程队承包地铁1号线的某段修建工作，从投标书中得知：甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的3倍；若由甲队先做20天，剩下的工程再由甲、乙两队合作10天完成．
（1）求甲、乙两队单独完成这项工程各需多少天？
（2）已知甲队每天的施工费用为15.6万元，乙队每天的施工费用为18.4万元，工程预算的施工费用为500万元，为缩短工期，拟安排甲、乙两队同时开工合作完成这项工程，那么工程预算的施工费用是否够用？若不够用，需增加多少万元？
【解析】解：（1）设乙队单独完成这项工程需x天，则甲队单独完成这项工作所需天数是3x天，
依题意得：+＝1，
解得x＝20，
检验，当x＝20时，3x≠0，
所以原方程的解为x＝20．
所以3x＝3×20＝60（天）．
答：乙队单独完成这项工程需20天，则甲队单独完成这项工作所需天数是60天；

（2）设甲、乙两队合作完成这项工程需要y天，
则有y（+）＝1，
解得y＝15．
需要施工的费用：15×（15.6+18.4）＝510（万元）．
∵510＞500，
∴工程预算的费用不够用，需要追加预算10万元．
11．（2022春•浦东新区校级期中）某汽车装配厂计划在规定的时限内组装汽车21辆，组装了6辆汽车后，又追加了组装5辆汽车的订单，要求交货时间不超过原来规定的期限，通过挖潜改革，提高工效，平均每天比原计划多组装2辆汽车，结果提前1天交货．问追加订单后，平均每天组装多少辆汽车？
【解析】解：设原计划平均每天组装x辆汽车，则追加订单后，平均每天组装（x+2）辆汽车．
由题意，得﹣﹣＝1，
整理，得x2+7x﹣30＝0，
解得：x＝3或x＝﹣10（负值舍去）．
经检验：x＝3是原方程的解．
当x＝3时，x+2＝3+2＝5．
答：追加订单后，平均每天组装5辆汽车．
七．一元一次不等式的应用（共3小题）
12．（2022•德城区模拟）某商场用60个A型包装袋与90个B型包装袋对甲，乙两类农产品进行包装出售（两种型号包装袋都用完），每个A型包装袋装2千克甲类农产品或装3千克乙类农产品，每个B型包装袋装3千克甲类农产品或装5千克乙类农产品，设有x个A型包装袋包装甲类农产品，有y个B型包装袋包装甲类农产品．
（1）请用含x或y的代数式填空完成表：
包装袋型号
A
B
甲类农产品质量（千克）
2x
　3y　
乙类农产品质量（千克）
　3（60﹣x）　
5（90﹣y）
（2）若甲、乙两类农产品的总质量分别是260千克与210千克，求x，y的值．
（3）若用于包装甲类农产品的B型包装袋数量是用于包装甲类农产品的A型包装袋数量的两倍，且它们数量之和不少于90个，记甲、乙两类农产品的总质量之和为m千克，求m的最小值与最大值．
【解析】解：（1）由题意可以填表如下：
包装袋型号
A
B
甲类农产品质量（千克）
2x
3y
乙类农产品质量（千克）
3（60﹣x）
5（90﹣y）
故答案为：3y；3（60﹣x）．
（2）由题意可得，，
解得．
∴即x的值为40；y的值为60．
（3）设有x个A型包装袋包装甲类农产品，则有y＝2x个B型包装袋包装甲类农产品．
∵用于包装甲类的A，B型包装袋的数量之和不少于90个，
∴x+2x≥90，
∴x≥30．
∵90﹣2x≥0，
∴x≤45；
∴30≤x≤45，
∴m＝2x+3（60﹣x）+6x+5（ 90﹣2x）＝﹣5x+630，
∵﹣5＜0，
∴当30＜x≤45时，m随x增大而减小，
∴当x＝45时，m有小值405，
当x＝30时，m有最大值480，
∴m的最大值为480，最小值为405．
13．（2022春•恩阳区 期中）某商店取厂家选购甲、乙两种商品，乙商品每件进价比甲商品每件进价多20元，若购进甲商品5件和乙商品4件共需要800元；
（1）求甲、乙两种商品每件的进价分别是多少元？
（2）若甲种商品的售价为每件100元，乙种商品的售价为每件125元，该商店准备购进甲、乙两种商品共40件，且这两种商品全部售出后总利润不少于900元，则甲种商品最多可购进多少件？
【解析】解：（1）设甲商品进价每件x元，乙商品进价每件y元，

解得，
答：甲商品进价每件80元，乙商品进价每件100元．

（2）设甲商品购进a件，则乙商品购进（40﹣a）件
a（100﹣80）+（40﹣a）（125﹣100）≥900
∴a≤20，
∵a为整数，
∴a最多为20．
答：甲商品最多购进20件．
14．（2018•葫芦岛）某爱心企业在政府的支持下投入资金，准备修建一批室外简易的足球场和篮球场，供市民免费使用，修建1个足球场和1个篮球场共需8.5万元，修建2个足球场和4个篮球场共需27万元．
（1）求修建一个足球场和一个篮球场各需多少万元？
（2）该企业预计修建这样的足球场和篮球场共20个，投入资金不超过90万元，求至少可以修建多少个足球场？
【解析】解：（1）设修建一个足球场x万元，一个篮球场y万元，根据题意可得：
，
解得：，
答：修建一个足球场和一个篮球场各需3.5万元，5万元；
（2）设足球场y个，则篮球场（20﹣y）个，根据题意可得：
3.5y+5（20﹣y）≤90，
解得：y≥，
答：至少可以修建7个足球场．
八．一元一次不等式组的整数解（共1小题）
15．（2022春•吉安月考）对m、n定义一种新运算“※”，规定：m※n＝am﹣bn+5（a．b均为非零常数），等式右边的运算是通常的四则运算，例如3※4＝3a﹣4b+5．已知2※3＝1，3※（﹣1）＝10．
（1）求a、b的值；
（2）若关于x的不等式组有且只有一个整数解，试求字母t的取值范围．
【解析】解：（1）∵2※3＝1，3※（﹣1）＝10，
∴，
解得：；
（2）∵不等式组，且a＝1，b＝2，
∴ax﹣b（2x﹣3）+5＝﹣3x+11＜9，3ax+6b+5＝3x+17＜t，
解得：，
∵关于x的不等式组有且只有一个整数解，
∴1＜≤2，
解得：20＜t≤23，
∴t的取值范围是20＜t≤23．