第29讲-抛物线-【高考培优直通车】2022年高三数学大一轮复习精品讲义（上海专用）

  第29讲-抛物线（解析版）

                                                                        教学内容

1.设是第二象限角，方程表示的曲线是（    ）

A. 焦点在轴上的椭圆    B. 焦点在轴上的椭圆

C. 焦点在轴上的双曲线   D. 焦点在轴上的双曲线

【答案】C

【解答】是第二象限角原方程化为

 易知：的系数为负，的系数为正，∴方程表示焦点在y轴上的双曲线.

2.过点（1，3）且渐近线为的双曲线方程是               .

【答案】

【解析】设所求双曲线为，将点代入得所以即为所求.

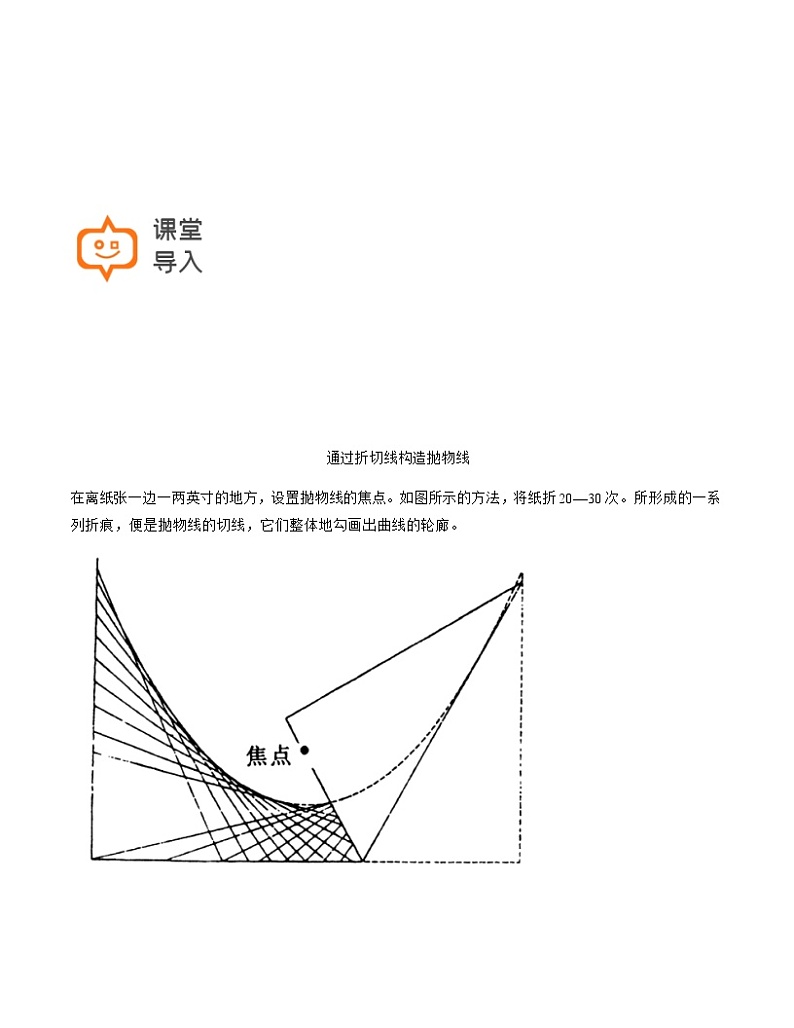
通过折切线构造抛物线

在离纸张一边一两英寸的地方，设置抛物线的焦点。如图所示的方法，将纸折20—30次。所形成的一系列折痕，便是抛物线的切线，它们整体地勾画出曲线的轮廊。

知识点一：抛物线的定义

知识梳理

平面内与一定点..和一条定直线（不在上）的距离相等的点P的轨迹叫做抛物线．点叫做抛物线的焦点，直线叫做抛物线的准线．

注意：当点在上时，上述表述的动点的轨迹是过点与垂直的直线．

例题精讲

例1：方程表示的曲线为（     ）

 【A】抛物线            【B】椭圆           【C】双曲线            【D】直线

【答案】D

【解析】

几何意义为：动点到定点和定直线的距离相等，

因为定点在定直线上，所以动点的轨迹为直线。

巩固练习

1．已知点，直线：，点是直线上的动点，若过垂直于轴的直线与

线段的垂直平分线交于点，则点所在曲线是         （ ）

【A】圆               【B】椭圆             【C】双曲线           【D】抛物线

【答案】D

【解析】由对称性可知：点到定点和定直线：的距离相等，

所以点的轨迹是抛物线。

2.动圆M与定直线相切，且与定圆：相外切，

求动圆圆心M的轨迹方程.

【答案】

【解析】设M（x，y），半径为r，则，且，

化简可得：，即圆心M的轨迹方程为．

知识点二：抛物线的标准方程

知识梳理

例题精讲

例题：

（1）以双曲线的中心为顶点，且以该双曲线的右焦点为焦点的抛物线方程是        ．

【答案】

（2）已知抛物线上的点到定点和到定直线的距离相等，则     .

 【答案】

（3）设某抛物线的准线与直线之间的距离为3，则该抛物线的方程为    .

【答案】或

巩固练习

1.若抛物线的顶点在原点，焦点和椭圆的右焦点重合，则抛物线的标准方程为         ．

【答案】

2.若抛物线的焦点与双曲线的右焦点重合，则该抛物线的准线方程为     ．

【答案】

3.在平面直角坐标系中，动点P和点M(-2,0)、N(2,0)满足，

则动点的轨迹方程为          .

【答案】

知识点三：抛物线的性质

知识梳理

设抛物线方程：，过焦点的直线（斜率存在且），对应倾斜角为，

与抛物线交于．

联立方程：，

整理可得：

则可得以下结论：

（1），；

（2），，；

（3）为定值；

（4）以为直径的圆和抛物线的准线相切于，以为直径的圆与相切于；

（5）

       ；

（6）；

（7），，三点共线；

（8）被抛物线平分．

例题精讲

例题1：设为抛物线的焦点，为抛物线上三点，若的重心与焦点重合，则的值是______________.

【答案】设，

可知抛物线的焦点是，根据抛物线的定义，

则．

例题2：设抛物线的焦点为，以为圆心，长为半径作一圆，与抛物线在轴

上方交于，则的值为  （  ）

8            18                    4

【答案】根据题意可作出图形如图所示，过分别向准线作垂线交于，

设，

则，且圆的方程为，

联立，可得

所以．

选A．

例题3：已知抛物线的焦点是，点在抛物线上，为坐标原点，若

点为的重心，的面积分别记为，则的值（ ）

【A】16             【B】48              【C】96              【D】192

【答案】B

【解析】以为底，为高，又为重心，

即

巩固练习

1.过抛物线的焦点作垂直于轴的直线，交抛物线于、两点，则以为圆心、为直径的圆方程是            ．

【答案】可知，所以，所以半径为2，此圆的方程为．

2.过抛物线的焦点作直线，交抛物线于两点，如果，

那么（    ）

A．8 B．10    C．6   D．4

【答案】A

3.若是抛物线的焦点，点在抛物线上，且，

则________.

【答案】200

例题精讲

例1：设为抛物线的焦点

（1）点，若点在抛物线上移动，则的最小值是__________。

（2）点，若点在抛物线上移动，则的最小值是__________．

（3）直线、直线，若点在抛物线上移动，则到和的距离

之和的最小值是__________．

【答案】   

例2：过抛物线的焦点作一条直线与抛物线相交于A、B两点，它们的横坐标之和

等于5，则这样的直线（    ）

A、有且仅有一条       B、有且仅有两条        C、有无穷多条         D、不存在

【答案】的焦点，若直线平行于y轴显然不满足题意．于是可设直线方程为

将直线方程代入抛物线方程可得，方程显然有两个实根，且两根之和为，两根之积为1，故两根都大于0，它们的横坐标之和．答案：B

例3：若动弦在抛物线上移动，但其中点横坐标始终是4，则的最大值为___.

解：设中点坐标为，，

显然，有，所以最大值为10.

巩固练习

1.已知抛物线的焦点为，定点的坐标为，若点为抛物线上的一点，到准线的距离为，且最小，求此时点坐标．

【答案】

2.点，抛物线（）的焦点为，若对于抛物线上的任意点，的最小值为41，则的值等于           ．

【答案】22或42

3.抛物线的焦点为F，点A、B在此抛物线上，且∠AFB＝90°，弦AB的中点M在其准线上的射影为M′，则的最大值为________．

【答案】

知识点四：直线与抛物线关系

知识梳理

例题精讲

例1：过点作倾斜角为的直线，与抛物线交于两点，则            ．

【答案】直线方程为，代入抛物线，得：，，，

则．

例2：在抛物线上求一点，使该点到直线的距离最短，该点的坐标是_______.

【答案】

例3：若抛物线上总存在关于直线对称的两点，求的范围 

【答案】设对称的两点分别为，中点，

考虑到直线应与垂直，设直线，

联立方程得，，所以，，

点也在上，所以，即

代入直线，得，所以方程化简为

考虑到，解得

巩固练习

1.若直线与抛物线仅有一个公共点，则实数          .

【答案】联立，可得，当时，满足题意；当时，

所以．综上或（二次项系数为0的情况不要忘记讨论）

2.设直线与抛物线相交于两点，与圆相切于点，且为线段的中点，若这样的直线恰有条，则的取值集合是________

【解析】设，由点差法得得，

，即，又，故，，所以，不符合题意，所以当存在时不存在这样的直线，而斜率存在时必有两条，故.

知识点五：综合问题

知识梳理

例题精讲

例1：已知抛物线的焦点，是抛物线上横坐标为，且位于轴上方的点，

到抛物线准线的距离是，过作垂直于轴，垂足为，中点为。

（1）求抛物线方程；

（2）过作，垂足为，求点坐标；

（3）以为圆心，为半径作圆，当是轴上的动点时，

讨论直线与圆的位置关系。

【解析】（1）；

（2）因为，由题意，，又因，故；而

故，则所在直线方程为，所在直线方程是，

解方程组，故。

（3）由条件，圆的圆心，半径为，当时，直线的方程为，

即，圆心到直线的距离是。令，

解得。故当时，直线与圆相离；同理，当时，直线与圆相切；时，直线与圆相交。

例2：已知动圆过定点，且与直线，其中.

（1）求动圆圆心的轨迹的方程；

（2）设A、B是轨迹上异于原点的两个不同点，直线OA和OB的倾斜角分别为和，当、变化且为定值时，证明直线AB恒过定点，并求出该定点坐标.

【答案】（1）由，解得动圆圆心的轨迹的方程为：.

（2）设，由题意得且，，

所以直线AB的斜率存在，设其方程为

由，得，     ①

（ⅰ）时，   ②

由①、②得，，.

所以直线AB的方程为，故直线AB恒过定点

（ⅱ）时，，.，得      ③

由①、③得，所以直线AB的方程为，

故直线AB恒过定点.

由（ⅰ）（ⅱ）知，当时，直线AB恒过定点；

当时，直线AB恒过定点.

巩固练习

1.抛物线的方程为，过抛物线上一点作斜率为、的两条

直线分别交抛物线于两点，（P、A、B三点互不相同），

且满足（且）.

（1）求抛物线的焦点坐标和准线方程；

（2）设直线AB上一点M，满足,求证：线段PM的中点在轴上；

（3）当时，若点P的坐标为，求为钝角时点A的纵坐标的取值范围.

【答案】（1）由   焦点为，准线方程为

（2）证明：点在抛物线上，

过点、的直线方程为，即

由，得

当时，，.同理

设点M的坐标为.

由，得，又，

，即，即线段PM的中点在轴上.

（3）由在抛物线上，所以，又，所以

根据（2）中，所以，

，，

为钝角或

又，当时，；

当时，，所以的取值范围是.

1．已知点P(2，y)在抛物线y2＝4x上，则点P到抛物线焦点F的距离为(　　)

A．2  B．3  C.  D.

答案　B

解析　因为抛物线y2＝4x的焦点为(1,0)，准线为x＝－1，结合定义点P到抛物线焦点的距离等于它到准线的距离，为3.

2．设O为坐标原点，直线x＝2与抛物线C：y2＝2px(p>0)交于D，E两点，若OD⊥OE，则C的焦点坐标为(　　)

A.  B.  C．(1,0)  D．(2,0)

答案　B

解析　方法一　∵抛物线C关于x轴对称，

∴D，E两点关于x轴对称．

可得出直线x＝2与抛物线的两交点的坐标分别为(2,2)，(2，－2)．

不妨设D(2,2)，E(2，－2)，

则＝(2,2)，＝(2，－2)．

又∵OD⊥OE，

∴·＝4－4p＝0，解得p＝1，

∴C的焦点坐标为.

方法二　∵抛物线C关于x轴对称，

∴D，E两点关于x轴对称．

∵OD⊥OE，∴D，E两点横、纵坐标的绝对值均相等．

不妨设点D(2,2)，将点D的坐标代入C：y2＝2px，

得4＝4p，解得p＝1，故C的焦点坐标为.

3．设F为抛物线y2＝2x的焦点，A，B，C为抛物线上三点，若F为△ABC的重心，则||＋||＋||的值为(　　)

A．1  B．2  C．3  D．4

答案　C

解析　依题意，设点A(x1，y1)，B(x2，y2)，C(x3，y3)，

又焦点F，所以x1＋x2＋x3＝3×＝，

则||＋||＋||＝＋＋＝(x1＋x2＋x3)＋＝＋＝3.

4．设抛物线的顶点为O，焦点为F，准线为l.P是抛物线上异于O的一点，过P作PQ⊥l于Q，则线段FQ的垂直平分线(　　)

A．经过点O   B．经过点P

C．平行于直线OP   D．垂直于直线OP

答案　B

解析　如图所示，P为抛物线上异于O的一点，

则|PF|＝|PQ|，

∴QF的垂直平分线经过点P.

5.给定抛物线：，F是的焦点，过点F的直线与相交于A、B两点.

（1）设的斜率为1，求与得夹角的大小.

（2）设，若，求在轴上的截距的变化范围.

【答案】（1）的焦点坐标为，直线的斜率为1，所以的方程为.

将代入方程，并整理得.

设，则有，.

设与的夹角为，则

所以与的夹角的大小为.

（2）由题设得，即，得，

因为，， 所以。联立解得：，依题意得，

所以或，又

得直线的方程为或

当时，在轴上的截距为或.

可知在上是递减的.故，

即直线在轴上的截距的变化范围为.

笔耕不辍