专题03 立体几何综合题-备战2022年上海高考数学模拟题分类汇编

专题03 立体几何综合题-备战2022年上海高考数学模拟题分类汇编

1．（2021年•黄浦区一模）已知正方体的棱长为4，点是侧面的中心．

（1）连接，求三棱锥的体积的数值；

（2）求异面直线与所成角的大小（结果用反三角函数值表示）．

2．（2021年•静安区一模）如图所示，等腰梯形是由正方形和两个全等的和组成，，．现将沿所在的直线折起，点移至点，使二面角的大小为．

（1）求四棱锥的体积；

（2）求异面直线与所成角的大小．

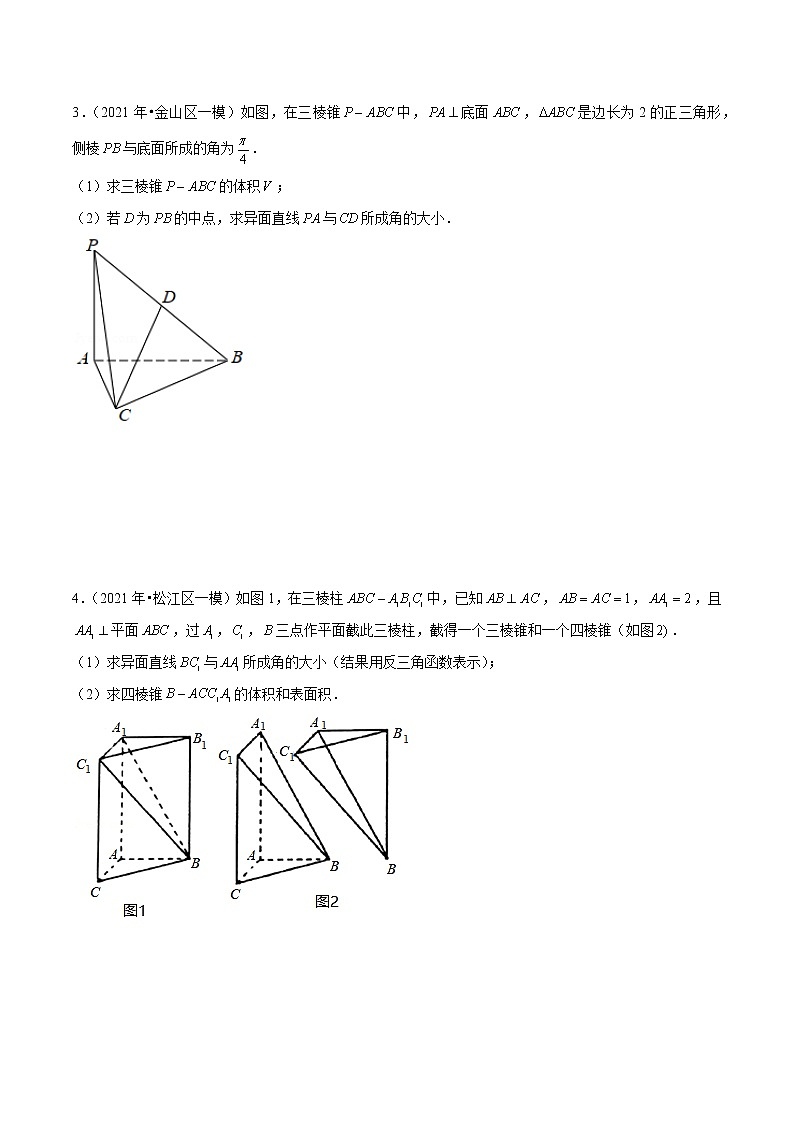
3．（2021年•金山区一模）如图，在三棱锥中，底面，是边长为2的正三角形，侧棱与底面所成的角为．

（1）求三棱锥的体积；

（2）若为的中点，求异面直线与所成角的大小．

4．（2021年•松江区一模）如图1，在三棱柱中，已知，，，且平面，过，，三点作平面截此三棱柱，截得一个三棱锥和一个四棱锥（如图．

（1）求异面直线与所成角的大小（结果用反三角函数表示）；

（2）求四棱锥的体积和表面积．

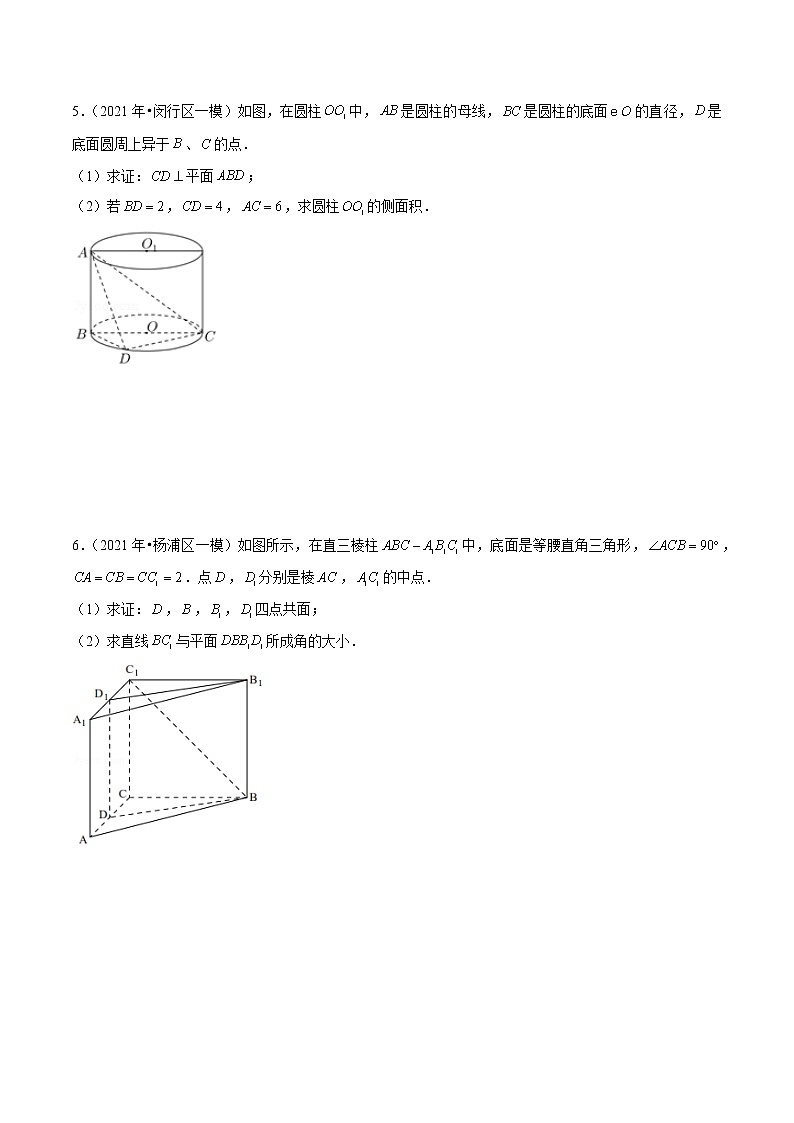
5．（2021年•闵行区一模）如图，在圆柱中，是圆柱的母线，是圆柱的底面的直径，是底面圆周上异于、的点．

（1）求证：平面；

（2）若，，，求圆柱的侧面积．

6．（2021年•杨浦区一模）如图所示，在直三棱柱中，底面是等腰直角三角形，，．点，分别是棱，的中点．

（1）求证：，，，四点共面；

（2）求直线与平面所成角的大小．

7．（2021年•浦东新区一模）如图，直三棱柱中，，，，点为线段的中点．

（1）求直三棱柱的体积；

（2）求异面直线与所成的角的大小．（结果用反三角表示）

8．（2021年•普陀区一模）某商场共有三层楼，在其圆柱形空间内安装两部等长的扶梯Ⅰ、Ⅱ供顾客乘用，如图，一顾客自一楼点处乘Ⅰ到达二楼的点处后，沿着二楼面上的圆弧逆时针步行至点处，且为弧的中点，再乘Ⅱ到达三楼的点处，设圆柱形空间三个楼面圆的中心分别为、、，半径为8米，相邻楼层的间距米，两部电梯与楼面所成角的大小均为．

（1）求此顾客在二楼面上步行的路程；

（2）求异面直线和所成角的大小．（结果用反三角函数值表示）

9．（2021•虹口区一模）如图在三棱锥中，棱、、两两垂直，，点在上，且．

（1）求异面直线和所成的角的大小；

（2）求三棱锥的体积．

10．（2021年•奉贤区一模）如图，在四棱锥中，已知平面，且四边形为直角梯形，，，．

（1）当四棱锥的体积为1时，求异面直线与所成角的大小；

（2）求证：平面．

11．（2021年•嘉定区一模）如图，正四棱柱的底面边长为2，．

（1）求该正四棱柱的表面积和体积；

（2）求异面直线与所成的角的大小（结果用反三角函数值表示）．

12．（2021秋•青浦区一模）如图，长方体中，，，点为的中点．

（1）求证：直线平面；

（2）求异面直线与所成角的大小．

13．（2021年•宝山区一模）如图，在长方体中，为上一点，已知，，，．

（1）求直线与平面所成角的大小（用反三角函数值表示）；

（2）求点到平面的距离．

14．（2021年•长宁区一模）如图，已知圆锥的顶点为，底面圆心为，高为，底面半径为2．

（1）求该圆锥的侧面积；

（2）设、为该圆锥的底面半径，且，为线段的中点，求直线与直线所成的角的正切值，

15．（2021年•徐汇区一模）如图，在直三棱柱中，，，，、分别为棱、的中点．

（1）求异面直线与所成的角的大小（结果用反三角函数值表示）；

（2）求五棱锥的体积．

16．（2021年•崇明区一模）如图，已知平面，，与平面所成的角为，且．

（1）求三棱锥的体积；

（2）设为的中点，求异面直线与所成角的大小（结果用反三角函数值表示）．

17．（2021•虹口区二模）在三棱锥中，，，是线段的中点，是线段的中点．

（1）求证：平面；

（2）求直线与平面所成的角的大小．

18．（2021•杨浦区二模）如图，棱柱中，，底面，是棱的中点．

（1）求证：直线与直线为异面直线；

（2）求直线与平面所成角的大小．

19．（2021•浦东新区二模）如图，已知圆锥底面圆的半径，直径与直径垂直，母线与底面所成的角为．

（1）求圆锥的侧面积；

（2）若为母线的中点，求二面角的大小（结果用反三角函数值表示）．

20．（2021•金山区二模）在长方体中，，过、、三点的平面截去长方体的一个角后，得到如图所示的几何体，且这个几何体的体积为10．

（1）求棱的长；

（2）求点到平面的距离．

21．（2021•闵行区二模）如图，在四棱锥中，已知平面，，，，且．

（1）求四棱锥的体积；

（2）求直线与平面所成的角．

22．（2021•普陀区二模）如图，设底面半径为2的圆锥顶点、底面中心依次为、，为其底面直径，点位于底面圆周上，且，异面直线与所成角的大小为．

（1）求此圆锥的体积；

（2）求二面角的大小．（结果用反三角函数值表示）

23．（2021•徐汇区二模）如图，在直三棱柱中，，．

（1）求异面直线与所成角的大小；

（2）若是棱的中点．求点到平面的距离．

24．（2021•长宁区二模）如图，是圆柱的一条母线，是圆柱的底面直径，在圆柱下底面圆周上，是线段的中点．已知，．

（1）求圆柱的侧面积；

（2）求证：．

25．（2021•黄浦区二模）已知长方体中，棱，，点是棱的中点．

（1）联结，求三棱锥的体积；

（2）求直线和平面所成角的大小．（结果用反三角函数值表示）

26．（2021•宝山区二模）如图，在四棱锥中，平面，是边长为2的正方形，，为侧棱的中点．

（1）求四棱锥的体积；

（2）求直线与平面所成角的正弦值．

27．（2021•奉贤区二模）已知、是正四棱柱的棱、的中点，异面直线与所成角的大小为．

（1）求证：、、、在同一平面上；

（2）求二面角的大小．

28．（2021•松江区二模）如图，是圆锥的顶点，是底面圆的圆心，、是底面圆的两条直径，且，，，为的中点．

（1）求异面直线与所成角的大小（结果用反三角函数值表示）；

（2）求点到平面的距离．

29．（2021•嘉定区二模）在矩形中，，，矩形绕旋转形成一个圆柱．如图，矩形绕顺时针旋转至，线段的中点为．

（1）求证：；

（2）求异面直线与所成的角的大小（结果用反三角函数值表示）．

30．（2021•崇明区二模）如图，直三棱柱中，，，，点为线段的中点．

（1）求直三棱柱的表面积；

（2）求异面直线与所成的角的大小．（结果用反三角函数值表示）