




所属成套资源:备战2022年新高考数学模拟试题分类汇编(福建专用)
专题12+立体几何综合题-备战2022年新高考数学模拟试题分类汇编(福建专用)
展开
这是一份专题12+立体几何综合题-备战2022年新高考数学模拟试题分类汇编(福建专用),文件包含专题12立体几何综合题解析版docx、专题12立体几何综合题原卷版docx等2份试卷配套教学资源,其中试卷共66页, 欢迎下载使用。
专题12 立体几何综合题
1.(2021•厦门一模)如图,在四棱锥中,侧面底面,侧面底面,,,,.
(1)证明:平面.
(2)当直线与平面所成的角最大时,求二面角的余弦值.
【答案】(1)见解析;(2)【详解】(1)证明:因为,,所以,因为平面平面,平面平面,所以平面,
又因为平面,所以,
平面平面,平面平面,
,所以平面,
因为平面,所以,
又因为,所以平面.
(2)解:由(1)知、、两两垂直,
建立如图所示的空间直角坐标系,设,,
则,因为,所以,
,,,,0,,,,,,0,,
平面的法向量为,
平面的法向量为,0,,
,
设直线与平面所成角大小为,二面角的大小为,
,
当,即时等号成立,取最大值.
由图可知为钝角,
所以,
故当直线与平面所成的角最大时,二面角的余弦值为.
2.(2021•龙岩一模)如图,四棱锥中,底面为矩形,侧面为等腰直角三角形,,,是的中点,二面角的大小为,设平面与平面的交线为.
(1)在线段上是否存在点,使平面?若存在,确定点的位置;若不存在,请说明理由;
(2)若点在上,直线与平面所成角的正弦值为,求线段的长.
【答案】(1)见解析;(2)
【详解】(1)因为底面为矩形,所以,
又因为平面,平面,
所以平面,
又因为平面平面,平面,
所以,从而.
取中点,连接,,
因为,所以,
因为、分别为矩形对边中点,所以,
所以平面,
因为,所以平面,
故当在点时,平面.
(2)建立如图所示的空间直角坐标系,
由(1)知为二面角的平面角,其大小为,
因为侧面为等腰直角三角形,,
所以,所以,,,,2,,,0,,,2,,
设,,,则,,,,2,,,,,
设平面的法向量为,,,
,令,,0,,
直线与平面所成角的正弦值为,
解得,
所以线段的长为.
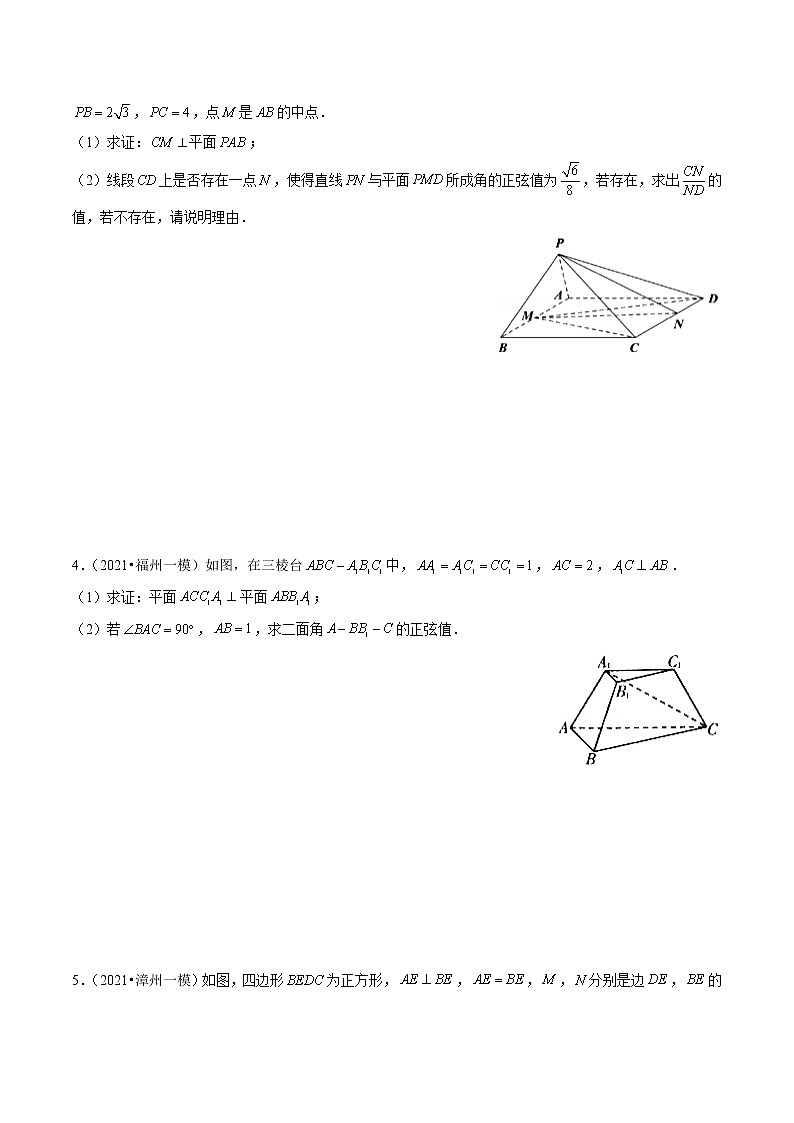
3.(2021•福建模拟)如图,在四棱锥中,底面是边长为4的菱形,,,,,点是的中点.
(1)求证:平面;
(2)线段上是否存在一点,使得直线与平面所成角的正弦值为,若存在,求出的值,若不存在,请说明理由.
【答案】(1)见解析;(2)1
【详解】(1)证明:在中,因为,,,所以,
因为点是的中点,所以,
在中,,,,
由余弦定理定理可得,,
故,所以,
在中,,,,所以,故,
又,,平面,所以平面;
(2)解:建立如图所示的空间直角坐标系,则,
设,0,,,
在中,,而,所以,故,
设平面的一个法向量为,直线与平面所成的角为,
因为,
所以,即,
令,则,
又,
所以,化简可得,解得或(舍,
故.
4.(2021•福州一模)如图,在三棱台中,,,.
(1)求证:平面平面;
(2)若,,求二面角的正弦值.
【答案】(1)见解析;(2)
【详解】(1)证明:由题意可知,四边形是等腰梯形,
过点作于点,过作于点,
则,
所以,所以,
则,
所以,
则△中,,所以△为直角三角形,且,
所以,因为,,,平面,
所以平面,因为平面,
所以平面平面;
(2)解:因为,,,,平面,
所以平面,又平面,所以,
过点作直线,以点为坐标原点建立空间直角坐标系如图所示,
则,
所以,
设平面的一个法向量为,
则有,即,
令,则,,所以,
由(1)可知,平面,
取为平面的一个法向量,
所以,
所以二面角的余弦值为,
故二面角的正弦值为.
5.(2021•漳州一模)如图,四边形为正方形,,,,分别是边,的中点,直线与平面所成的角为.
(1)求证:平面;
(2)求二面角的余弦值.
【答案】(1)见解析;(2)【详解】(1)证明:,,,、平面,
平面,
平面平面,
点在平面的射影在线段上,
为直线与平面所成的角,即,
又,为等边三角形,
连接,,
为的中点,,
平面,平面,,
又,、平面,平面,
平面,,
,,,
,
,,,
,、平面,
平面.
(2)解:分别取,的中点为,,连接,,则,
由(1)知,平面,平面,,
为等边三角形,,
平面,平面,
,
又,、平面,平面,
,
,,两两垂直,
故以为原点,,,所在直线分别为,,轴建立如图所示空间直角坐标系,
设,则,1,,,0,,,0,,,,,,,,,,,
,,,,1,,
设平面的法向量为,,,则,即,
不妨设,则,,,
由(1)可得,,为平面的一个法向量,
,,
由图知,二面角的平面角为锐角,
二面角的余弦值为.
6.(2021•泉州一模)如图,在四棱锥中,二面角是直二面角,为等腰直角三角形的斜边,,,,为线段上的动点.
(1)当时,证明:平面;
(2)若平面平面,求二面角的余弦值.
【答案】(1)见解析;(2)
【详解】(1)证明:如图,连接交于,,,
,且为的中点,连接,
,为的中点,则,
平面,平面,
平面;
(2)解:由(1)知,,若平面平面,
以为坐标原点,以所在直线为轴,以所在直线为轴,
在平面内,过作垂直于底面的直线为轴,建立空间直角坐标系,
在中,由,,,可得,则,
由等面积法求得,再由,可得,
求解三角形可得,,
故,0,,,0,,,,,,,,
,,,
,设,
,,,,
,
设平面的一个法向量为,
由,
取,得;
而平面的一个法向量为,
平面平面,,解得.
,,,,,,,
设平面的一个法向量为,
由,取,得,
取平面的一个法向量为,
.
由图可知,二面角为锐二面角,则二面角的余弦值为.
7.(2021•福建模拟)如图,四棱锥的底面为矩形,是边上的点,,.
(1)求证:平面平面;
(2)求直线和平面所成角的正弦值.
【答案】(1)见解析;(2)
【详解】(1)证明:在上取点,使,连接,交于,连接、、,
因为为矩形,,所以为正方形,所以,
因为,,,所以,所以,
又为因为中点,所以,
又因为,所以平面,
又因为平面,所以平面平面;
(2)解:建立如图所示的空间直角坐标系,不妨设,
则,,,
于是,0,,,3,,,3,,,1,,
,2,,,3,,,1,,
设平面的法向量为,,,
,令,,,,
所以直线和平面所成角的正弦值为.
8.(2021•新高考Ⅰ)如图,在三棱锥中,平面平面,,为的中点.
(1)证明:;
(2)若是边长为1的等边三角形,点在棱上,,且二面角的大小为,求三棱锥的体积.
【答案】(1)见解析;(2)
【详解】(1)证明:因为,为的中点,所以,
又平面平面,平面平面,平面,
所以平面,又平面,
所以;
(2)方法一:
取的中点,因为为正三角形,所以,
过作与交于点,则,
所以,,两两垂直,
以点为坐标原点,分别以,,为轴,轴,轴建立空间直角坐标系如图所示,
则,,,,,1,,
设,0,,则,
因为平面,故平面的一个法向量为,
设平面的法向量为,
又,
所以由,得,
令,则,,故,
因为二面角的大小为,
所以,
解得,所以,
又,所以,
故.
方法二:
过作,交于点,过作于点,连结,
由题意可知,,又平面
所以平面,又平面,
所以,又,
所以平面,又平面,
所以,
则为二面角的平面角,即,
又,
所以,则,
故,
所以,
因为,
则,
所以,则,
所以,则,
所以.
9.(2021•漳州模拟)如图,在四棱锥中,侧面底面,底面是直角梯形,,,,,.
(1)证明:平面平面;
(2)在线段上是否存在点,使得直线与平面所成角的正弦值为?若存在,求出线段的长度;若不存在,请说明理由.
【答案】(1)见解析;(2)或
【详解】(1)证明:因为平面平面,且平面平面,
因为,平面,
所以平面,
又因为平面,
所以平面平面;
(2)解:在平面内,过点作交于点,则可知平面,
以点为坐标原点建立空间直角坐标系如图所示,
由,,,
故点,
所以,
设为平面的法向量,
则有,即,
取,则,,
故,
设,
则,
因为直线与平面所成角的正弦值为,
则,
解得或,
故存在点满足题意,此时或.
10.(2021•福建模拟)如图,在中,,,,,,沿将点折至处,使得,点为的中点.
(1)证明:平面.
(2)求二面角的余弦值.
【答案】(1)见解析;(2)
【详解】(1)证明:由,,且,平面,平面,
可得平面,因此.
由,,得,
因此,,由勾股定理可得.
又因为点为的中点,所以,
而,平面,平面,故平面.
(2)解:因为,,,平面,平面,
所以平面,又,所以平面.
如图,以为原点,建立空间直角坐标系,则,,,
易知是平面的一个法向量.
设平面的法向量为,则,即,
令,得,
易知二面角为锐角,故二面角的余弦值为.
11.(2021•福建模拟)如图,直角三角形所在的平面与半圆弧所在平面相交于,,,分别为,的中点是上异于,的点,.
(1)证明:平面平面
(2)若点为半圆弧上的一个三等分点(靠近点,求二面角的余弦值.
【答案】(1)见解析;(2)
【详解】证明:(1)因为半圆弧上的一点,所以.
在中,,分别为,的中点,所以,且.
于是在中,,
所以为直角三角形,且.
因为,,所以.
因为,,,
所以平面.
又平面,所以平面平面.
解:(2)由已知,以为坐标原点,分别以垂直于平面向上的方向,
向量所在方向作为轴、轴、轴的正方向,建立如图所示的空间直角坐标系,
则,,0,,,,,,,,
,,.
设平面的一个法向量为,,,
则,取,得,1,.
设平面的法向量,,,
则,即,取,得.
所以,
又二面角为锐角,所以二面角的余弦值为.
12.(2021•福州模拟)在三棱柱中,,平面平面,平面平面.
(1)证明:平面;
(2)在①,②与平面所成的角为,③异面直线与所成角的余弦值为.这三个条件中任选两个,求二面角的余弦值.
【答案】(1)见解析;(2)
【详解】(1)证明:,平面平面,平面平面,平面,
平面,
又平面,
,
同理,,
又,
平面;
(2)若选择①②,由(1)知,平面,所以三棱柱是直三棱柱,
,,
,
在直三棱柱中,平面,,
平面,
为与平面所成角,
,
在△中,,,所以,
在中,,所以,
以为坐标原点,,,所在直线分别为轴,轴,轴建立如图所示的空间直角坐标系,
则,
,
设平面的一个法向量为,则,可取,
设平面的一个法向量为,则,可取,
,
二面角的余弦值为;
若选②③,由(1)知,平面,所以三棱柱是直三棱柱,
在直三棱柱中,平面,,
平面,
为与平面所成角,
,
在直三棱柱中,,,
异面直线与所成角为,所以,
在△中,设,则,所以,
在中,因为,所以,
以为坐标原点,,,所在直线分别为轴,轴,轴建立如图所示的空间直角坐标系,
则,
,
设平面的一个法向量为,则,可取,
设平面的一个法向量为,则,可取,
,
二面角的余弦值为;
若选①③,因为,,所以,
由(1)知,平面,则,
在三棱柱中,,
所以异面直线与所成角为,所以,
在中,因为,所以,
以为坐标原点,,,所在直线分别为轴,轴,轴建立如图所示的空间直角坐标系,
则,
,
设平面的一个法向量为,则,可取,
设平面的一个法向量为,则,可取,
,
二面角的余弦值为;
13.(2021•泉州二模)如图1,在等腰直角三角形中,是斜边上的高.以为折痕把折起,使点到达点的位置,且,,,分别为,,的中点,为的中点,如图2.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
【答案】(1)见解析;(2)
【详解】(1)证明:连结交于点,连结,
因为,分别为,的中点,
所以为的重心,故,
又为的中点,为的中点,
所以,即,
所以,
又平面,平面,
所以平面;
(2)解:由题意可知,,,又,,平面,
所以平面,故以点为坐标原点,建立空间直角坐标系如图所示,
设,则,,
所以,
设平面的法向量为,
则,
令,则,
所以,
故直线与平面所成角的正弦值为.
14.(2021•莆田二模)已知正方形的边长为2,沿将折起至位置(如图),为的重心,点在边上,且.
(1)证明:平面;
(2)若,求二面角的余弦值.
【答案】(1)见解析;(2)
【详解】(1)证明:连结交于点,连结,,
因为为的重心,所以,
又因为,所以,
故,又平面,平面,
故平面;
(2)解:因为,,所以,
又在中,为的中点,
所以为等腰三角形,所以,
延长交于点,则,
所以,所以,
又因为,,
所以,,互相垂直,建立空间直角坐标系如图所示,
则,0,,,0,,,,,,0,,,,,
因为为上靠近点的三等分点,所以,
因为为的重心,故,
设平面的法向量为,
因为,
故,则,
令,则,
同理可得平面的法向量为,
则有.
故二面角的余弦值为.
15.(2021•厦门模拟)在三棱柱中,是上一点,是的中点,且平面.
(1)证明:;
(2)若平面,平面平面,,求直线与平面所成角的正弦值.
【答案】(1)见解析;(2)
【详解】(1)证明:连结,,因为四边形是平行四边形,
所以,,三点共线,且是的中点,
因为平面平面,又平面,且平面,
所以,所以是的中点,即;
(2)解:因为平面,所以,,
因为平面平面,所以即为二面角的平面角,
因为平面平面,所以,故,,两两垂直,
以点为坐标原点,建立空间直角坐标系如图所示,
因为,,所以,设,
则,,
所以,
设平面的法向量为,
则,即,
令,则,故,
所以,
故直线与平面所成角的正弦值为.
16.(2021•宁德三模)如图,在平面四边形中,且,分别将、沿直线翻转为、,不重合),连结,,.
(1)求证:;
(2)若,,点在平面内的正投影为的重心,求二面角的余弦值.
【答案】(1)见解析;(2)
【详解】(1)证明:取中点,连接,,,,
因为,所以,
又因为为沿折起的图形,所以,
又,,,平面,
所以平面,又平面,
所以,
又因为为中点,
所以;
(2)解:由(1)得,,,为中点,
所以,,三点共线,且,
以点为坐标原点,建立空间直角坐标系如图所示,
因为,,
又,所以,,
又点在平面内的正投影为的重心,
所以,
故,
设平面的一个法向量为,
则,即
令,则,,故,
设平面的一个法向量为,,
则,即
令,则,,故,
所以,
由图可知二面角为锐角,
所以二面角的余弦值为.
17.(2021•福建模拟)如图,在四棱锥中,平面,,,,.过点做四棱锥的截面,分别交,,于点,,,已知,.
(1)求直线与平面所成的角;
(2)求证:为线段的中点.
【答案】(1);(2)见解析
【详解】(1)解:过点作与平行的射线,以为轴,以为轴,为轴,
建立如图空间直角坐标系如图所示,
则有,0,,,,,,3,,,3,,,0,,,,2,,
设平面的法向量为,因为,
则,即,
令,则,,故,
又,设直线与平面所成的角的大小为,
则
所以,即直线与平面所成的角的大小为;
(2)证明:在上取点,且满足,
连接,,则,且,
因为,所以,且,
所以是平行四边形,
所以,
又因为平面,平面,所以平面,
因为平面平面,所以,
所以,因为,所以,即为线段中点,
所以为线段的中点.
18.(2021•南平模拟)如图,已知四边形为菱形,,,是的中点,平面平面.
(1)证明:平面;
(2)若平面平面,,求与平面所成角的正弦值.
【答案】(1)见解析;(2)
【详解】(1)证明:已知四边形为菱形,,所以是等边三角形,
因为是的中点,所以,
又,,,平面,
所以平面
又菱形中,,平面,平面,
所以平面.
而平面,平面平面,得.
因此平面.
(2)解:因为平面平面,平面平面,,平面,
所以平面,
于是,,两两互相垂直,以为坐标原点,以,,所在直线分别为轴,轴,轴建立空间直角坐标系.
则,0,,,0,,,2,,,,
所以,,,
设平面的法向量,
由,得,可取,
所以.
故与平面所成角的正弦值.
19.(2021•龙岩模拟)如图,在三棱柱中,为棱的中点,,,,.
(1)求证:平面;
(2)求二面角的余弦值.
【答案】(1)见解析;(2)
【详解】(1)证明:在三棱柱中,为棱的中点,,,
,又,、平面,
平面,
又平面,,
,..
,,
,,平面,
平面.
(2)以为原点,为轴,为轴,为轴,建立空间直角坐标系,
则,0,,,2,,,1,,
过作平面,垂足为,连接,,
则,,四边形是平行形,
且,,
,2,,
,2,,,2,,,1,,
设平面的法向量,,,
则,取,得,2,,
设平面的法向量,,,
则,取,得,1,,
设二面角的平面角为,
则.
二面角的余弦值为.
20.(2021•鼓楼区校级模拟)木工技艺是我国传统文化瑰宝之一,体现了劳动人民的无穷智慧.很多古代建筑和家具保存到现代依然牢固,这其中,有连接加固功能的“楔子”发挥了重要作用.
如图,楔子状五面体的底面为一个矩形,,,平面,棱,设,分别是,的中点.
(1)证明:,,,四点共面,且平面平面;
(2)若二面角的大小为,求直线与平面所成角的正弦值.
【答案】(1)见解析;(2)
【详解】(1)证明:因为平面,且平面,
又平面平面,所以,
又,分别为矩形两边,的中点,
所以,则,
故,,,四点共面;
因为,所以,
又因为,,,平面,
所以平面,又平面,
则平面平面;
(2)解:在平面内,过点作于,平面,
由(1)可知,平面平面,平面平面,
所以平面,又因为,,
则二面角的平面角为,,
在和中,,,
所以,
过作边的垂线交,于点,,
以为坐标原点,建立空间直角坐标系如图所示,
则,
所以,
,
设平面的法向量为,
则,即,
令,则,故,
设直线与平面所成的角为,
则,
所以直线与平面所成角的正弦值为.
21.(2021•福建模拟)如图,在四棱锥中,平面平面,平面平面,四边形为直角梯形,其中,,,是的中点.
(1)求证:;
(2)若,求直线与平面所成的角的正弦值.
【答案】(1)见解析;(2)
【详解】(1)证明:连接,
由已知,为中点,
又,故四边形为正方形,
所以知,
面面,
又面面,,平面,
平面,故.
同理可证,
又,故平面,
连接,可知,
又,,
可知平面,
又平面,
,
由已知,故四边形为平行四边形,
故,
可知.
(2)解:以为坐标原点,分别以的正方向为,;轴的正方向建立空间直角坐标系,
由,知,不妨设,
则可知,0,,,0,,,1,,
,,
设平面的法向量为,
则,
令,则,
,
又,1,,故,
设与平面所成的角为,则.
22.(2021•漳州模拟)如图,在四棱锥中,四边形是菱形,,,三棱锥是正三棱锥,,分别为,的中点.
(1)证明:直线平面;
(2)求二面角的余弦值.
【答案】(1)见解析;(2)
【详解】(1)证明:连结,交于点,连结,
因为四边形是菱形,
所以为的中点,
因为为的中点,
所以,
又因为平面,平面,
所以直线平面.
(2)解:作平面于,则为正的中心,在线段上,
且,,,.
因为四边形是菱形,所以,
以为坐标原点,分别以,,的方向为轴,轴,轴的正方向建立空间直角坐标系,如图,
则,,,,,,,
所以,,,
设是平面的法向量,
则,取,
设是平面的法向量,
则,取,
所以,
又因为二面角是锐二面角,
所以二面角的余弦值为.
23.(2021•福建模拟)如图,在四棱锥中,四边形为平行四边形,以为直径的圆为圆心)过点,且,底面,为的中点.
(1)证明:平面平面;
(2)求二面角的余弦值
【答案】(1)见解析;(2)
【详解】(1)证明:由题意点为圆上一点,则
由底面,知,
又,、平面,平面,
平面,,
为的中点,,
,平面,
平面,平面平面.
(2)如图,以为原点,为轴,为轴,为轴,建立空间直角坐标系,
则,2,,,2,,,1,,,1,,
,0,,,1,,
设平面的法向量,,,
则,取,得,,,
由(1)知平面,
则平面的一个法向量,1,,
,
由图可知二面角的锐角,
则二面角的余弦值为.
24.(2021•福建模拟)如图,在五面体中,四边形为矩形,为等边三角形,且平面平面,和平面所成的角为,且点在平面上的射影落在四边形的中心,且.
(1)证明:平面;
(2)求平面与平面所成角(锐角)的余弦值.
【答案】(1)见解析;(2)
【详解】(1)证明:连接,取,的中点分别为,,连接,,,易得为四边形的中心,
所以平面,
设,因为和平面所成的角为,所以,因为,所以,
又因为平面平面,平面平面,,
所以平面,,则,,
所以四边形是平行四边形,所以.
因为平面,平面,
所以平面;
(2)解:
在平面中,作,
如图,以为坐标原点,,,所在直线分别为,,轴建系,
则,
又因为平面平面,所以是平面的一个法向量.
设平面的法向量为,
因为,
所以,解得,
所以平面的法向量为.
记平面与平面所成的角为,
所以,
所以平面与平面所成角(锐角)的余弦值为.
25.(2021•龙岩模拟)如图,四棱锥中,底面是菱形,,是棱上的点,是中点,且底面,.
(1)求证:;
(2)若,求二面角的余弦值.
【答案】(1)见解析;(2)
【详解】(1)证明:在菱形中,,所以为等边三角形,
又因为为的中点,所以,
又因为,所以,
因为底面,平面,所以,
因为,,平面,所以平面,
因为是棱上的点,所以平面,所以;
(2)解:因为底面,,建立空间直角坐标系如图所示,
设,则,
所以,
则,由,
所以,
设平面的法向量为,
则有,即,
令,则,故,
又因为平面的法向量为,
所以,
由图可知,二面角为锐二面角,
所以二面角的余弦值为.
26.(2021•三明模拟)如图,在四棱锥中,底面为等腰梯形,且,,点在平面内的正投影点在上,若为等边三角形,为的中点.
(1)求证:平面;
(2)求二面角的大小.
【答案】(1)见解析;(2)
【详解】(1)证明:连接,
为等边三角形,为的中点,
,
点在平面内的正投影点在上,
平面,
平面,,
又,、平面,
平面,,
在等腰梯形中,,,
,
由余弦定理知,,
,即,
,
又平面,平面,
平面.
(2)解:以为原点,,所在直线分别为,轴,作平面,建立如图所示的空间直角坐标系,则,,,,,,,0,,
由题意知,,,
,,
是棱长为2的等边三角形,,
,
,,,
,,,,,,,,,
设平面的法向量为,,,则,即,
令,则,,,1,,
同理可得,平面的法向量为,1,,
,,
由图可知,二面角为钝角,
二面角的大小为.
27.(2021•厦门二模)在三棱锥中,是的重心,是面内一点,且平面.
(1)画出点的轨迹,并说明理由;
(2)平面,,,,当最短时,求二面角的余弦值.
【答案】(1)见解析;(2)
【详解】解;(1)分别取,三等分点,,其中,,
连接,,,则为点的轨迹.
①,,,
平面,平面,平面,
是的重心,,
平面,平面,平面,
,平面平面,
当在上时,平面.
②如图,假设不在上,任取上一点,连接,
平面,平面,,
平面平面,则平面,
平面平面,平面,,
得,与矛盾,故假设不成立.
综上所述,为点的轨迹;
(2)由余弦定理得,
解得,
,即,
,,
平面,,
,平面,,平面,
平面,,当点与重合时,最短.
如图,在平面内,作,
以为坐标原点,为轴,为轴,为轴,建立直角坐标系,
则,,0,,,0,,,
,,,,
设为平面的一个法向量,
则,令,得,
设为平面的一个法向量,
则,令,符,
,
二面角的余弦值为.
28.(2021•福州模拟)如图,在五面体中,底面四边形为正方形,平面平面.
(1)求证:;
(2)若,,,,求平面与平面所成的锐二面角的余弦值.
【答案】(1)见解析;(2)
【详解】证明:(1)在正方形中,,
平面,平面,
平面,
又平面,且平面,
.
(2)四边形为正方形,
,
,
平面,
平面,
,
又,以为坐标原点,分别以,,所在直线分别为,,轴建立空间直角坐标系,如图所示,
则,3,,,3,,,1,,
可知,1,为平面的一个法向量,
设平面的一个法向量为,
,则,令,,
设平面与平面所成的锐二面角为,
则,
故平面与平面所成的锐二面角的余弦值为.
29.(2021•福建模拟)在三棱柱中,,分别为,的中点.
(1)证明:平面;
(2)若,,且在底面上的正投影恰为点,求二面角的正弦值.
【答案】(1)见解析;(2)
【详解】(1)证明:如图,连接,,
因为为的中点,且四边形是平行四边形,
所以为的中点,又为的中点,
所以,
又因为平面,且平面,
所以;
(2)由(1)可得二面角即为二面角,
如图,连接,,
由在底面上的正投影恰为,
所以平面,
因此,,又因为,且为的中点,
故,即线段,,两两垂直,
以为坐标原点,,,所在的直线分别为,,轴建立如图所示的空间直角坐标系,
则,0,,,0,,,,,,1,,,0,,
对于平面,因为平面,且平面,
所以平面的一个法向量为,0,,
设平面的法向量为,,,
因为,2,,,0,,
由,可得,
取,则,0,,
设二面角的平面角为,
则,
因此二面角的正弦值为.
30.(2021•南安市校级二模)如图,矩形和梯形所在平面互相垂直,,,,.
(1)求证:平面;
(2)当的长为何值时,直线与平面所成角的大小为.
【答案】(1)见解析;(2)的长为时,直线与平面所成角的大小为
【详解】(1)由已知可得,,,
且、面,、面.
面面,
面,平面;
(2)如图,以为原点,建立空间直角坐标系,
,,
则,
,.,
,.
则,0,,,0,,,,,,,,,0,.
,,
设面的法向量为,
,,
直线与平面所成角的大小为.,.
的长为时,直线与平面所成角的大小为.
相关试卷
这是一份专题12 立体几何综合题-备战2022年新高考数学模拟试题分类汇编(江苏专用),文件包含专题12立体几何综合题解析版docx、专题12立体几何综合题原卷版docx等2份试卷配套教学资源,其中试卷共56页, 欢迎下载使用。
这是一份专题12+立体几何综合题-备战2022年新高考数学模拟试题分类汇编(广东专用),文件包含专题12立体几何综合题解析版docx、专题12立体几何综合题原卷版docx等2份试卷配套教学资源,其中试卷共60页, 欢迎下载使用。
这是一份专题15+导数综合题-备战2022年新高考数学模拟试题分类汇编(福建专用),文件包含专题15导数压轴题解析版docx、专题15导数压轴题原卷版docx等2份试卷配套教学资源,其中试卷共52页, 欢迎下载使用。









