2020年新疆乌鲁木齐市第六十八中学第二次模拟考试数学试卷(word版含答案)

2020年乌鲁木齐市第六十八中学第二次模拟考试

数学试卷

满分：150分 考试时间：120分钟

注意事项：

1．答题前填写好自己的姓名、班级、考号等信息

2．请将答案正确填写在答题卡上

第I卷（选择题）

一、单选题(每小题5分，共45分)

1．下列实数中最小的是（       ）

A．－ B．－3 C．－ D．－2

2．如图是由若干个完全相同的小正方体组合而成的几何体，若将小正方体①移动到小正方体②的正上方，下列关于移动后几何体的三视图说法正确的是（　　）

A．左视图发生变化 B．俯视图发生变化

C．主视图发生改变 D．三个视图都发生改变

3．如图，直线l1∥l2，且分别与直线l交于C，D两点，把一块含30°角的三角尺按如图所示的位置摆放，若∠1＝58°，则∠2的度数为(     )

A．92° B．98° C．102° D．122°

4．下列计算正确的是（       ）．

A． B．

C． D．

5．《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等．交易其一，金轻十三两．问金、银一枚各重几何？”．意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相等．两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计）．问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，根据题意得（　　）

A．

B．

C．

D．

6．如图，在中，以点为心，适当长度为半径画弧，分别交、于点．再分别以点．为圆心，大于的长为半径画弧．两弧交于点．作射线交边于点．过点作于点，若，，，则的长度为（ ）

A． B．

C． D．

7．如图，点A、B、C、D、E在⊙O上，的度数为60°，则∠B+∠D的度数是（     ）

A．180° B．120° C．100° D．150°

8．二次函数的图象如图，对称轴为直线，关于的一元二次方程（为实数）在的范围内有解，则的取值范围是（       ）

A． B． C． D．

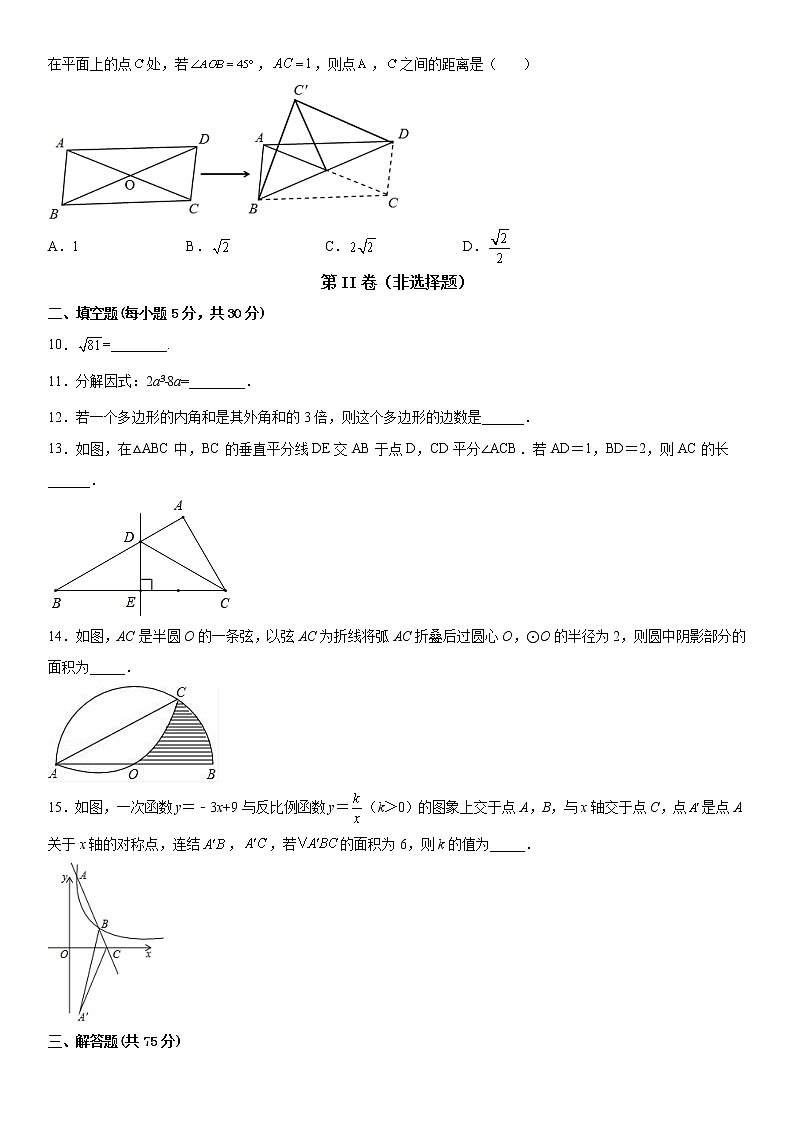
9．如图，平行四边形纸片的对角线与相交于点，将平行四边形纸片沿对角线拆叠，使点落在平面上的点处，若，，则点，之间的距离是（       ）

A．1 B． C． D．

第II卷（非选择题）

二、填空题(每小题5分，共30分)

10．=________.

11．分解因式：2a3﹣8a=________．

12．若一个多边形的内角和是其外角和的3倍，则这个多边形的边数是______．

13．如图，在△ABC中，BC的垂直平分线DE交AB于点D，CD平分∠ACB．若AD＝1，BD＝2，则AC的长______．

14．如图，AC是半圆O的一条弦，以弦AC为折线将弧AC折叠后过圆心O，⊙O的半径为2，则圆中阴影部分的面积为_____．

15．如图，一次函数y＝﹣3x+9与反比例函数y＝（k＞0）的图象上交于点A，B，与x轴交于点C，点是点A关于x轴的对称点，连结，，若的面积为6，则k的值为_____．

三、解答题(共75分)

16．（6分）解不等式组，并写出该不等式组的整数解．

17．（6分）先化简，再求值：，其中x满足．

18．（8分）如图，矩形ABCD的对角线AC，BD相交于点O，点E，F分别是AB，CD上的点，且AE=CF，连接DE，BF．

(1)求证：四边形FBED是平行四边形；

(2)已知AO=6，∠ADB=30°，求AD的长．

19．（8分）“大千故里，文化内江”，我市某中学为传承大千艺术精神，征集学生书画作品．王老师从全校20个班中随机抽取了4个班，对征集作品进行了数量分析统计，绘制了如下两幅不完整的统计图．

（1）王老师采取的调查方式是　　（填“普查”或“抽样调查”），王老师所调查的4个班共征集到作品　　件，并补全条形统计图；

（2）在扇形统计图中，表示班的扇形周心角的度数为　　；

（3）如果全校参展作品中有4件获得一等奖，其中有1名作者是男生，3名作者是女生．现要从获得一等奖的作者中随机抽取两人去参加学校的总结表彰座谈会，求恰好抽中一男一女的概率．（要求用树状图或列表法写出分析过程）

20．（10分）二七纪念塔位于郑州市二七广场，是独特的仿古，它是为纪念京汉铁路工人大罢工而修建的纪念性建筑物．学完三角函数知识后，某校”数学社团”的刘明和王华决定用自己学到的知识测量二七纪念塔的高度．如图，CD是高为1米的测角仪，在D处测得塔顶端A的仰角为，向塔方向前进38米在E处测得塔顶端A的仰角为，求二七纪念塔AB的高度（精确到1米，参考数据）．

21．（12分）随着地摊经济的火爆发展，某小龙虾养殖户决定将自家养殖的小龙虾加工后拿到夜市售卖，已知每份小龙虾的成本价是元，在投放市场试销后，发现每晚销售量（份）与销售单价（元/份）是一次函数的关系，部分数据如下：

（1）求与之间的函数表达式．

（2）求该养殖户每晚的销售利润（元）与销售单价（元/份）的函数表达式．（利润收入-成本）

（3）若相关部门规定一件产品的利润率不得高于，则当销售单价定为多少元时每晚可获利最大？并求出最大利润．

22．（12分）如图，是的直径，是上一点，是的中点，为延长线上一点，且，与交于点，与交于点．

（1）求证：是的切线；

（2）若，，求直径的长．

23．（13分）已知抛物线经过三点，直线交抛物线于A､D两点，交y轴于点G．

（1）求抛物线的解析式；

（2）点P是直线AD上方抛物线上的一点，作轴，垂足为F，交AD于点N，且点N将线段PF分为的两部分．

①求点P的坐标；

②过点P作于点M，若直线l到直线AD的距离是PM的2倍，请直接写出直线l的解析式．

参考答案：

1．A

2．C

3．A

4．D

5．D

6．C

7．D

8．D

9．D

10．9

11．2a（a+2）（a﹣2）

12．8

13．

14．

15．6

16．不等式组的解集为-2≤x＜1，整数解为-2，-1，0．

17．；.

18．(1)

(2)AD的长为

19．（1）抽样调查；24；

（2）150°；（3）恰好抽中一男一女的概率为．

20．二七纪念塔AB的高度约为62米

21．（1）；

（2）；

（3）当销售单价定为元时每晚可获利最大，且每晚的最大利润为元．

22．（1）

（2）直径的长为20．

23．（1）；（2）①点或；②直线l的表达式为：或或或