四川省成都市第二十三中学2022年中考试题猜想数学试卷含解析

这是一份四川省成都市第二十三中学2022年中考试题猜想数学试卷含解析，共25页。试卷主要包含了考生要认真填写考场号和座位序号，下列各数中比﹣1小的数是，如图图形中是中心对称图形的是等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
注意事项
1．考生要认真填写考场号和座位序号。
2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。
3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
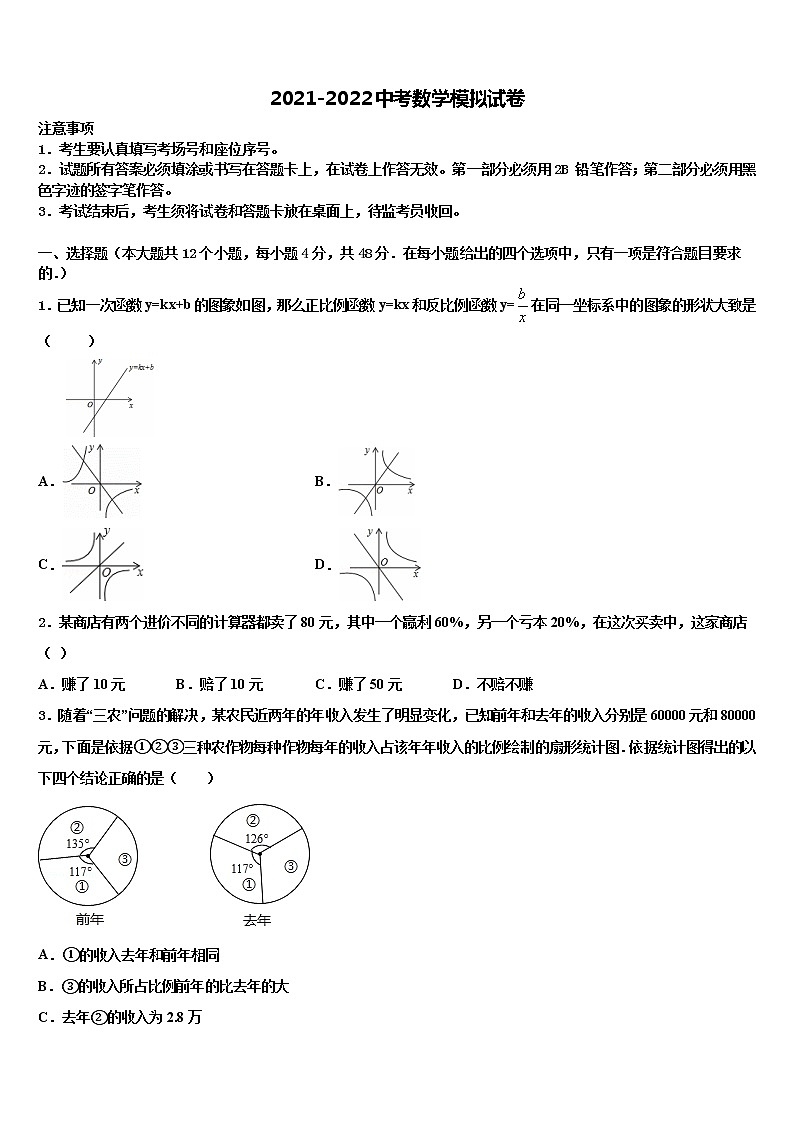
1．已知一次函数y=kx+b的图象如图，那么正比例函数y=kx和反比例函数y=在同一坐标系中的图象的形状大致是（ ）

A． B．
C． D．
2．某商店有两个进价不同的计算器都卖了80元，其中一个赢利60%，另一个亏本20%，在这次买卖中，这家商店（ ）
A．赚了10元 B．赔了10元 C．赚了50元 D．不赔不赚
3．随着“三农”问题的解决，某农民近两年的年收入发生了明显变化，已知前年和去年的收入分别是60000元和80000元，下面是依据①②③三种农作物每种作物每年的收入占该年年收入的比例绘制的扇形统计图．依据统计图得出的以下四个结论正确的是（　　）

A．①的收入去年和前年相同
B．③的收入所占比例前年的比去年的大
C．去年②的收入为2.8万
D．前年年收入不止①②③三种农作物的收入
4．如图，BC是⊙O的直径，A是⊙O上的一点，∠B＝58°，则∠OAC的度数是( )

A．32° B．30° C．38° D．58°
5．如图，把一块直角三角板的直角顶点放在直尺的一边上，若∠1=50°，则∠2的度数为（ ）．

A．50° B．40° C．30° D．25°
6．下列各数中比﹣1小的数是（　　）
A．﹣2 B．﹣1 C．0 D．1
7．正五边形绕着它的中心旋转后与它本身重合，最小的旋转角度数是（　　）
A．36° B．54° C．72° D．108°
8．已知不透明的袋中只装有黑、白两种球，这些球除颜色外都相同，其中白球有30个，黑球有n个．随机地从袋中摸出一个球，记录下颜色后，放回袋子中并摇匀，再从中摸出一个球，经过如此大量重复试验，发现摸出的黑球的频率稳定在0.4附近，则n的值约为（ ）
A．20 B．30 C．40 D．50
9．如图，是由7个大小相同的小正方体堆砌而成的几何体，若从标有①、②、③、④的四个小正方体中取走一个后，余下几何体与原几何体的主视图相同，则取走的正方体是（　　）

A．① B．② C．③ D．④
10．如图图形中是中心对称图形的是（　　）
A． B．
C． D．
11．三角形的两边长分别为3和6，第三边的长是方程x2﹣6x+8＝0的一个根，则这个三角形的周长是（　　）
A．9 B．11 C．13 D．11或13
12．如图是抛物线y=ax2+bx+c（a≠0）的图象的一部分，抛物线的顶点坐标是A（1，4），与x轴的一个交点是B（3，0），下列结论：①abc＞0；②2a+b=0；③方程ax2+bx+c=4有两个相等的实数根；④抛物线与x轴的另一个交点是（﹣2.0）；⑤x（ax+b）≤a+b，其中正确结论的个数是（　　）

A．4个 B．3个 C．2个 D．1个
二、填空题：（本大题共6个小题，每小题4分，共24分．）
13．因式分解：3x3﹣12x=_____．
14．点 C 在射线 AB上，若 AB=3，BC=2，则AC为_____．
15．如图，在等腰中，，点在以斜边为直径的半圆上，为的中点．当点沿半圆从点运动至点时，点运动的路径长是________．

16．如图，折叠长方形纸片ABCD，先折出对角线BD，再将AD折叠到BD上，得到折痕DE，点A的对应点是点F，若AB=8，BC=6，则AE的长为_____．

17．已知，在同一平面内，∠ABC＝50°，AD∥BC，∠BAD的平分线交直线BC于点E，那么∠AEB的度数为__________．
18．在一次射击比赛中，某运动员前7次射击共中62环，如果他要打破89环（10次射击）的记录，那么第8次射击他至少要打出_____环的成绩．
三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19．（6分）如图，⊙O是△ABC的外接圆，FH是⊙O的切线，切点为F，FH∥BC，连结AF交BC于E，∠ABC的平分线BD交AF于D，连结BF．（1）证明：AF平分∠BAC；（2）证明：BF=FD；（3）若EF=4，DE=3，求AD的长．

20．（6分）在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点的位置如图所示．现将△ABC平移，使点A变换为点D，点E、F分别是B、C的对应点．
请画出平移后的△DEF．连接AD、CF，则这两条线段之间的关系是________．
21．（6分）如图，在矩形纸片ABCD中，AB=6，BC=1．把△BCD沿对角线BD折叠，使点C落在C′处，BC′交AD于点G；E、F分别是C′D和BD上的点，线段EF交AD于点H，把△FDE沿EF折叠，使点D落在D′处，点D′恰好与点A重合．

（1）求证：△ABG≌△C′DG；
（2）求tan∠ABG的值；
（3）求EF的长．
22．（8分）如图，梯形ABCD中，AD∥BC，DC⊥BC，且∠B=45°，AD=DC=1，点M为边BC上一动点，联结AM并延长交射线DC于点F，作∠FAE=45°交射线BC于点E、交边DCN于点N，联结EF．
（1）当CM：CB=1：4时，求CF的长．
（2）设CM=x，CE=y，求y关于x的函数关系式，并写出定义域．
（3）当△ABM∽△EFN时，求CM的长．

23．（8分）为实施“农村留守儿童关爱计划”，某校结全校各班留守儿童的人数情况进行了统计，发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况，并制成如下两幅不完整的统计图：
求该校平均每班有多少名留守儿童？并将该条形统计图补充完整；某爱心人士决定从只有2名留守儿童的这些班级中，任选两名进行生活资助，请用列表法或画树状图的方法，求出所选两名留守儿童来自同一个班级的概率．
24．（10分）如图，为的直径，，为上一点，过点作的弦，设．

（1）若时，求、的度数各是多少？
（2）当时，是否存在正实数，使弦最短？如果存在，求出的值，如果不存在，说明理由；
（3）在（1）的条件下，且，求弦的长．
25．（10分）某学校2017年在某商场购买甲、乙两种不同足球，购买甲种足球共花费2000元，购买乙种足球共花费1400元，购买甲种足球数量是购买乙种足球数量的2倍．且购买一个乙种足球比购买一个甲种足球多花20元；求购买一个甲种足球、一个乙种足球各需多少元；2018年这所学校决定再次购买甲、乙两种足球共50个．恰逢该商场对两种足球的售价进行调整，甲种足球售价比第一次购买时提高了10%，乙种足球售价比第一次购买时降低了10%．如果此次购买甲、乙两种足球的总费用不超过2910元，那么这所学校最多可购买多少个乙种足球？
26．（12分）如图所示，一幢楼房AB背后有一台阶CD，台阶每层高0.2米，且AC＝17.2米，设太阳光线与水平地面的夹角为α，当α＝60°时，测得楼房在地面上的影长AE＝10米，现有一老人坐在MN这层台阶上晒太阳．（取1.73）
（1）求楼房的高度约为多少米？
（2）过了一会儿，当α＝45°时，问老人能否还晒到太阳？请说明理由．

27．（12分）在中，，以为直径的圆交于，交于.过点的切线交的延长线于．求证：是的切线．




参考答案

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1、C
【解析】
试题分析：如图所示，由一次函数y=kx+b的图象经过第一、三、四象限，可得k＞1，b＜1．因此可知正比例函数y=kx的图象经过第一、三象限，反比例函数y=的图象经过第二、四象限．综上所述，符合条件的图象是C选项．
故选C．

考点：1、反比例函数的图象；2、一次函数的图象；3、一次函数图象与系数的关系
2、A
【解析】
试题分析：第一个的进价为：80÷(1+60%)=50元，第二个的进价为：80÷(1－20%)=100元，则80×2－(50+100)=10元，即盈利10元.
考点：一元一次方程的应用
3、C
【解析】
A、前年①的收入为60000×=19500，去年①的收入为80000×=26000，此选项错误；
B、前年③的收入所占比例为×100%=30%，去年③的收入所占比例为×100%=32.5%，此选项错误；
C、去年②的收入为80000×=28000=2.8（万元），此选项正确；
D、前年年收入即为①②③三种农作物的收入，此选项错误，
故选C．
【点睛】
本题主要考查扇形统计图，解题的关键是掌握扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数，并且通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系．
4、A
【解析】
根据∠B＝58°得出∠AOC=116°,半径相等，得出OC=OA，进而得出∠OAC=32°，利用直径和圆周角定理解答即可．
【详解】
解：∵∠B＝58°,
∴∠AOC=116°,
∵OA=OC，
∴∠C=∠OAC=32°,
故选：A．
【点睛】
此题考查了圆周角的性质与等腰三角形的性质．此题比较简单，解题的关键是注意数形结合思想的应用．
5、B
【解析】
解：如图，由两直线平行，同位角相等，可求得∠3=∠1=50°，
根据平角为180°可得，∠2=90°﹣50°=40°．
故选B．

【点睛】
本题考查平行线的性质，掌握两直线平行，同位角相等是解题关键．
6、A
【解析】
根据两个负数比较大小，绝对值大的负数反而小，可得答案．
【详解】
解：A、﹣2＜﹣1，故A正确；
B、﹣1＝﹣1，故B错误；
C、0＞﹣1，故C错误；
D、1＞﹣1，故D错误；
故选：A．
【点睛】
本题考查了有理数大小比较，利用了正数大于0，0大于负数，注意两个负数比较大小，绝对值大的负数反而小．
7、C
【解析】
正五边形绕着它的中心旋转后与它本身重合，最小的旋转角度数是=72度，
故选C．
8、A
【解析】
分析：根据白球的频率稳定在0.4附近得到白球的概率约为0.4,根据白球个数确定出总个数,进而确定出黑球个数n.
详解：根据题意得: , 
计算得出:n=20, 
故选A.
点睛：根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
9、A
【解析】
根据题意得到原几何体的主视图，结合主视图选择．
【详解】
解：原几何体的主视图是：
．
视图中每一个闭合的线框都表示物体上的一个平面，左侧的图形只需要两个正方体叠加即可．
故取走的正方体是①．
故选A．
【点睛】
本题考查了简单组合体的三视图,中等难度,作出几何体的主视图是解题关键.
10、B
【解析】
把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形.
【详解】
解：根据中心对称图形的定义可知只有B选项是中心对称图形，故选择B.
【点睛】
本题考察了中心对称图形的含义.
11、C
【解析】
试题分析：先求出方程x2－6x＋8＝0的解，再根据三角形的三边关系求解即可.
解方程x2－6x＋8＝0得x=2或x=4
当x=2时，三边长为2、3、6，而2+3＜6，此时无法构成三角形
当x=4时，三边长为4、3、6，此时可以构成三角形，周长=4+3+6=13
故选C.
考点：解一元二次方程，三角形的三边关系
点评：解题的关键是熟记三角形的三边关系：任两边之和大于第三边，任两边之差小于第三边.
12、B
【解析】
通过图象得到、、符号和抛物线对称轴，将方程转化为函数图象交点问题，利用抛物线顶点证明.
【详解】
由图象可知，抛物线开口向下，则，，
抛物线的顶点坐标是，
抛物线对称轴为直线，
，
，则①错误，②正确；
方程的解，可以看做直线与抛物线的交点的横坐标，
由图象可知，直线经过抛物线顶点，则直线与抛物线有且只有一个交点，
则方程有两个相等的实数根，③正确；
由抛物线对称性，抛物线与轴的另一个交点是，则④错误；
不等式可以化为，
抛物线顶点为，
当时，，
故⑤正确.
故选：.
【点睛】
本题是二次函数综合题，考查了二次函数的各项系数与图象位置的关系、抛物线对称性和最值，以及用函数的观点解决方程或不等式.

二、填空题：（本大题共6个小题，每小题4分，共24分．）
13、3x（x+2）（x﹣2）
【解析】
先提公因式3x，然后利用平方差公式进行分解即可．
【详解】
3x3﹣12x
=3x（x2﹣4）
=3x（x+2）（x﹣2），
故答案为3x（x+2）（x﹣2）．
【点睛】
本题考查了提公因式法与公式法分解因式，要求灵活使用各种方法对多项式进行因式分解，一般来说，如果可以先提取公因式的要先提取公因式，再考虑运用公式法分解．
14、2或2．
【解析】
解：本题有两种情形：
（2）当点C在线段AB上时，如图，∵AB=3，BC=2，∴AC=AB﹣BC=3-2=2；

（2）当点C在线段AB的延长线上时，如图，∵AB=3，BC=2，∴AC=AB+BC=3+2=2．

故答案为2或2．
点睛：在未画图类问题中，正确画图很重要，本题渗透了分类讨论的思想，体现了思维的严密性，在今后解决类似的问题时，要防止漏解．
15、π
【解析】
取的中点，取的中点，连接，，，则，故的轨迹为以为圆心，为半径的半圆弧，根据弧长公式即可得轨迹长.
【详解】
解：如图，取的中点，取的中点，连接，，，

∵在等腰中，，点在以斜边为直径的半圆上，
∴，
∵为的中位线，
∴，
∴当点沿半圆从点运动至点时，点的轨迹为以为圆心，为半径的半圆弧，
∴弧长，
故答案为：.
【点睛】
本题考查了点的轨迹与等腰三角形的性质.解决动点问题的关键是在运动中，把握不变的等量关系(或函数关系)，通过固定的等量关系(或函数关系)，解决动点的轨迹或坐标问题.
16、3
【解析】
先利用勾股定理求出BD，再求出DF、BF，设AE=EF=x．在Rt△BEF中，由EB2=EF2+BF2，列出方程即可解决问题．
【详解】
∵四边形ABCD是矩形，∴∠A=90°．
∵AB=8，AD=6，∴BD1．
∵△DEF是由△DEA翻折得到，∴DF=AD=6，BF=2．设AE=EF=x．在Rt△BEF中，∵EB2=EF2+BF2，∴（8﹣x）2=x2+22，解得：x=3，∴AE=3．
故答案为：3．

【点睛】
本题考查了矩形的性质、勾股定理等知识，解题时，我们常常设要求的线段长为x，然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．
17、65°或25°
【解析】
首先根据角平分线的定义得出∠EAD=∠EAB，再分情况讨论计算即可．
【详解】
解：分情况讨论：(1)∵AE平分∠BAD，

∴∠EAD=∠EAB，
∵AD∥BC，
∴∠EAD=∠AEB，
∴∠BAD=∠AEB，
∵∠ABC＝50°，
∴∠AEB= •（180°-50°）=65°．
(2)∵AE平分∠BAD，

∴∠EAD=∠EAB= ，
∵AD∥BC，
∴∠AEB=∠DAE=，∠DAB=∠ABC,
∵∠ABC＝50°，
∴∠AEB= ×50°=25°．
故答案为:65°或25°.
【点睛】
本题考查平行线的性质、角平分线的定义等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
18、8
【解析】
为了使第8次的环数最少,可使后面的2次射击都达到最高环数,即10环.
设第8次射击环数为x环,根据题意列出一元一次不等式
62+x+2×10＞89
解之,得
x＞7
x表示环数,故x为正整数且x＞7,则
x的最小值为8
即第8次至少应打8环.
点睛：本题考查的是一元一次不等式的应用.解决此类问题的关键是在理解题意的基础上,建立与之相应的解决问题的“数学模型”——不等式,再由不等式的相关知识确定问题的答案.

三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19、【小题1】 见解析
【小题2】 见解析
【小题3】
【解析】
证明：（1）连接OF
∴FH切·O于点F
∴OF⊥FH ………………………… 1分
∵BC | | FH
∴OF⊥BC ………………………… 2分
∴BF="CF" ………………………… 3分
∴∠BAF=∠CAF
即AF平分∠BAC…………………4分
（2） ∵∠CAF=∠CBF
又∠CAF=∠BAF
∴∠CBF=∠BAF ………………………… 6分
∵BD平分∠ABC
∴∠ABD=∠CBD
∴∠BAF+∠ABD=∠CBF+∠CBD
即∠FBD=∠FDB………………………… 7分
∴BF="DF" ………………………… 8分
（3） ∵∠BFE=∠AFB ∠FBE=∠FAB
∴ΔBEF∽ΔABF………………………… 9分
∴即BF2=EF·AF …………………… 10分
∵EF=4 DE=3 ∴BF="DF" =4+3=7
AF=AD+7
即4（AD+7）=49 解得AD=
20、见解析
【解析】
(1)如图：

(2)连接AD、CF，则这两条线段之间的关系是AD＝CF，且AD∥CF．
21、（1）证明见解析（2）7/24（3）25/6
【解析】（1）证明：∵△BDC′由△BDC翻折而成，
∴∠C=∠BAG=90°，C′D=AB=CD，∠AGB=∠DGC′，∴∠ABG=∠ADE。
在△ABG≌△C′DG中，∵∠BAG=∠C，AB= C′D，∠ABG=∠AD C′，
∴△ABG≌△C′DG（ASA）。
（2）解：∵由（1）可知△ABG≌△C′DG，∴GD=GB，∴AG+GB=AD。
设AG=x，则GB=1﹣x，
在Rt△ABG中，∵AB2+AG2=BG2，即62+x2=（1﹣x）2，解得x=。
∴。
（3）解：∵△AEF是△DEF翻折而成，∴EF垂直平分AD。∴HD=AD=4。
∵tan∠ABG=tan∠ADE=。∴EH=HD×=4×。
∵EF垂直平分AD，AB⊥AD，∴HF是△ABD的中位线。∴HF=AB=×6=3。
∴EF=EH+HF=。
（1）根据翻折变换的性质可知∠C=∠BAG=90°，C′D=AB=CD，∠AGB=∠DGC′，故可得出结论。
（2）由（1）可知GD=GB，故AG+GB=AD，设AG=x，则GB=1-x，在Rt△ABG中利用勾股定理即可求出AG的长，从而得出tan∠ABG的值。
（3）由△AEF是△DEF翻折而成可知EF垂直平分AD，故HD=AD=4，再根据tan∠ABG的值即可得出EH的长，同理可得HF是△ABD的中位线，故可得出HF的长，由EF=EH+HF即可得出结果。
22、 (1) CF=1；（2）y=，0≤x≤1；（3）CM=2﹣．
【解析】
（1）如图1中，作AH⊥BC于H．首先证明四边形AHCD是正方形，求出BC、MC的长，利用平行线分线段成比例定理即可解决问题；
（2）在Rt△AEH中，AE2=AH2+EH2=12+（1+y）2，由△EAM∽△EBA，可得，推出AE2=EM•EB，由此构建函数关系式即可解决问题；
（3）如图2中，作AH⊥BC于H，连接MN，在HB上取一点G，使得HG=DN，连接AG．想办法证明CM=CN，MN=DN+HM即可解决问题；
【详解】
解：（1）如图1中，作AH⊥BC于H．

∵CD⊥BC，AD∥BC，
∴∠BCD=∠D=∠AHC=90°，
∴四边形AHCD是矩形，
∵AD=DC=1，
∴四边形AHCD是正方形，
∴AH=CH=CD=1，
∵∠B=45°，
∴AH=BH=1，BC=2，
∵CM=BC=，CM∥AD，
∴=，
∴=，
∴CF=1．
（2）如图1中，在Rt△AEH中，AE2=AH2+EH2=12+（1+y）2，
∵∠AEM=∠AEB，∠EAM=∠B，
∴△EAM∽△EBA，
∴=，
∴AE2=EM•EB，
∴1+（1+y）2=（x+y）（y+2），
∴y=，
∵2﹣2x≥0，
∴0≤x≤1．
（3）如图2中，作AH⊥BC于H，连接MN，在HB上取一点G，使得HG=DN，连接AG．

则△ADN≌△AHG，△MAN≌△MAG，
∴MN=MG=HM+GH=HM+DN，
∵△ABM∽△EFN，
∴∠EFN=∠B=45°，
∴CF=CE，
∵四边形AHCD是正方形，
∴CH=CD=AH=AD，EH=DF，∠AHE=∠D=90°，
∴△AHE≌△ADF，
∴∠AEH=∠AFD，
∵∠AEH=∠DAN，∠AFD=∠HAM，
∴∠HAM=∠DAN，
∴△ADN≌△AHM，
∴DN=HM，设DN=HM=x，则MN=2x，CN=CM=x，
∴x+x=1，
∴x=﹣1，
∴CM=2﹣．
【点睛】
本题考查了正方形的判定与性质，平行线分线段成比例定理，勾股定理，相似三角形的判定与性质，全等三角形的判定与性质.熟练运用平行线分线段成比例定理是解（1）的关键；证明△EAM∽△EBA是解（2）的关键；综合运用全等三角形的判定与性质是解（3）的关键.
23、解：（1）该校班级个数为4÷20%=20（个），
只有2名留守儿童的班级个数为：20﹣（2+3+4+5+4）=2（个），
该校平均每班留守儿童的人数为：
=4（名），
补图如下：

（2）由（1）得只有2名留守儿童的班级有2个，共4名学生．设A1，A2来自一个班，B1，B2来自一个班，

有树状图可知，共有12中等可能的情况，其中来自一个班的共有4种情况，
则所选两名留守儿童来自同一个班级的概率为：=．
【解析】
（1）首先求出班级数，然后根据条形统计图求出只有2名留守儿童的班级数，再求出总的留守儿童数，最后求出每班平均留守儿童数；
（2）利用树状图确定可能种数和来自同一班的种数，然后就能算出来自同一个班级的概率.
24、（1）， ;（2）见解析；（3）．
【解析】
（1）连结AD、BD,利用m求出角的关系进而求出∠BCD、∠ACD的度数;
（2）连结,由所给关系式结合直径求出AP，OP，根据弦CD最短，求出∠BCD、∠ACD的度数，即可求出m的值．
（3）连结AD、BD，先求出AD，BD，AP，BP的长度，利用△APC∽△DPB和△CPB∽△APD得出比例关系式，得出比例关系式结合勾股定理求出CP，PD，即可求出CD．
【详解】
解：（1）如图1，连结、．

是的直径
，
又，
，
（2）如图2，连结．

，，
，则，
解得

要使最短，则于
，

，

，
故存在这样的值，且；
（3）如图3，连结、．

由（1）可得，
，，
，
，，
，

，
①，
②
同理
，
③，
由①得，由③得
，
在中，，
，

由②，得，
．
【点睛】
本题考查了相似三角形的判定与性质和锐角三角函数关系和圆周角定理等知识，掌握圆周角定理以及垂径定理是解题的关键．
25、（1）购买一个甲种足球需要50元，购买一个乙种篮球需要1元（2）这所学校最多可购买2个乙种足球
【解析】
（1）根据题意可以列出相应的分式方程，从而可以求得购买一个甲种足球、一个乙种足球各需多少元；
（2）根据题意可以列出相应的不等式，从而可以求得这所学校最多可购买多少个乙种足球．
【详解】
（1）设购买一个甲种足球需要x元，则购买一个乙种篮球需要（x+2）元，
根据题意得：，
解得：x＝50，
经检验，x＝50是原方程的解，且符合题意，
∴x+2＝1．
答：购买一个甲种足球需要50元，购买一个乙种篮球需要1元．
（2）设可购买m个乙种足球，则购买（50﹣m）个甲种足球，
根据题意得：50×（1+10%）（50﹣m）+1×（1﹣10%）m≤2910，
解得：m≤2．
答：这所学校最多可购买2个乙种足球．
【点睛】
本题考查分式方程的应用，一元一次不等式的应用，解答此类问题的关键是明确题意，列出相应的分式方程和一元一次不等式，注意分式方程要检验，问题（2）要与实际相联系．
26、（1）楼房的高度约为17.3米；（2）当α＝45°时，老人仍可以晒到太阳．理由见解析.
【解析】
试题分析：（1）在Rt△ABE中，根据的正切值即可求得楼高；（2）当时，从点B射下的光线与地面AD的交点为F,与MC的交点为点H.可求得AF=AB=17.3米，又因CF=CH=17.3-17.2=0.1米，CM=0.2，所以大楼的影子落在台阶MC这个侧面上.即小猫仍可晒到太阳.
试题解析：解：（1）当当时，在Rt△ABE中，
∵,
∴BA=10tan60°=米.
即楼房的高度约为17.3米.

当时，小猫仍可晒到太阳.理由如下：
假设没有台阶，当时，从点B射下的光线与地面AD的交点为F,与MC的交点为点H.
∵∠BFA=45°，
∴,此时的影长AF=BA=17.3米，
所以CF=AF-AC=17.3-17.2=0.1.
∴CH=CF=0.1米，
∴大楼的影子落在台阶MC这个侧面上.
∴小猫仍可晒到太阳.
考点：解直角三角形.
27、证明见解析．
【解析】
连接OE，由OB=OD和AB=AC可得，则OF∥AC，可得，由圆周角定理和等量代换可得，由SAS证得，从而得到，即可证得结论．
【详解】
证明：如图，连接，
∵，
∴，
∵，
∴，
∴，
∴，
∴
∵
∴，则，
∴，
∴，即，
在和中，
∵，
∴，
∴
∵是的切线，则，
∴，
∴，则，
∴是的切线．

【点睛】
本题主要考查了等腰三角形的性质、切线的性质和判定、圆周角定理和全等三角形的判定与性质，熟练掌握圆周角定理和全等三角形的判定与性质是解题的关键．