专题19【精品】 阿基米德折弦定理-2022年中考数学几何模型解题策略研究（课件+讲义）

专题19 阿基米德折弦定理

一、方法突破

【问题呈现】

阿基米德，公元前公元前212年，古希腊）是有史以来最伟大的数学家之一，他与牛顿、高斯并称为三大数学王子．

折弦定义:从圆周上任一点出发的两条弦，所组成的折线，我们称之为该图的一条折弦。

阿基米德折弦定理：一个圆中一条由两长度不同的弦组成的折弦所对的两段弧的中点在较长弦上的射影，就是折弦的中点。

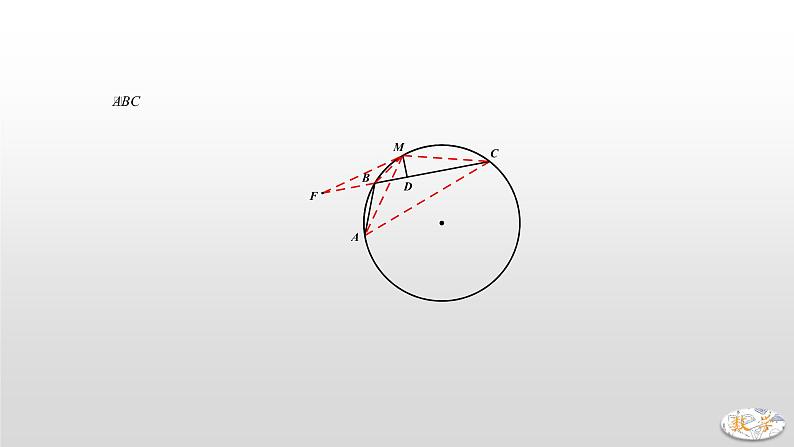
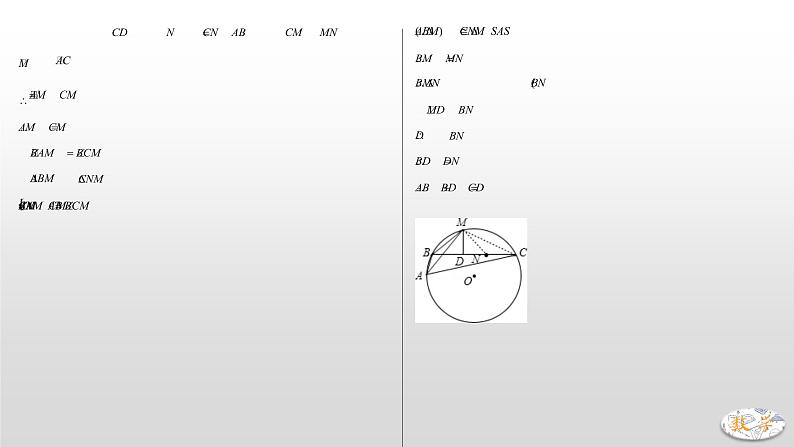
​   如下图所示，AB和BC是⊙O的两条弦(即ABC是圆的一条折弦)，BC>AB，M是 的中点，则从M向BC所作垂线之垂足D是折弦ABC的中点，即CD=AB+BD。

【证明方法】

方法1:补短法

如图，延长DB至F，使BF=BA

∵M是的中点

∴∠MCA=∠MAC=∠MBC

∵M、B、A、C四点共圆

∴∠MCA+∠MBA=180°

∵∠MBC+∠MBF=180°

∴∠MBA=∠MBF

∵MB=MB,BF=BA

∴△MBF≌△MBA

∴∠F=∠MAB=∠MCB

∴MF=MC

∵MD⊥CF

∴CD=DF=DB+BF=AB+BD

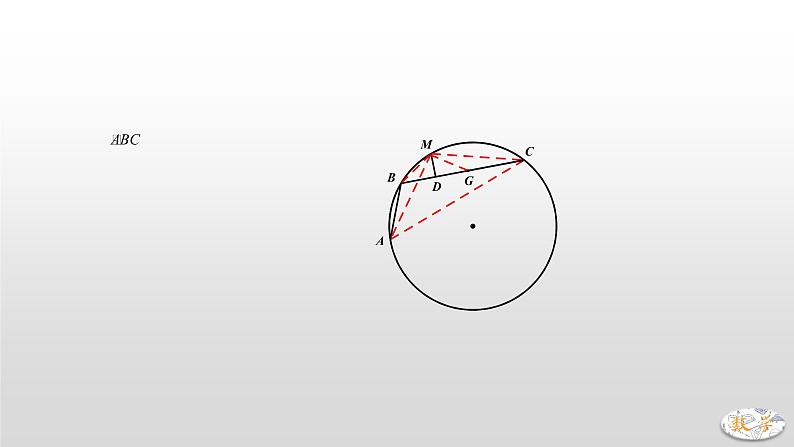
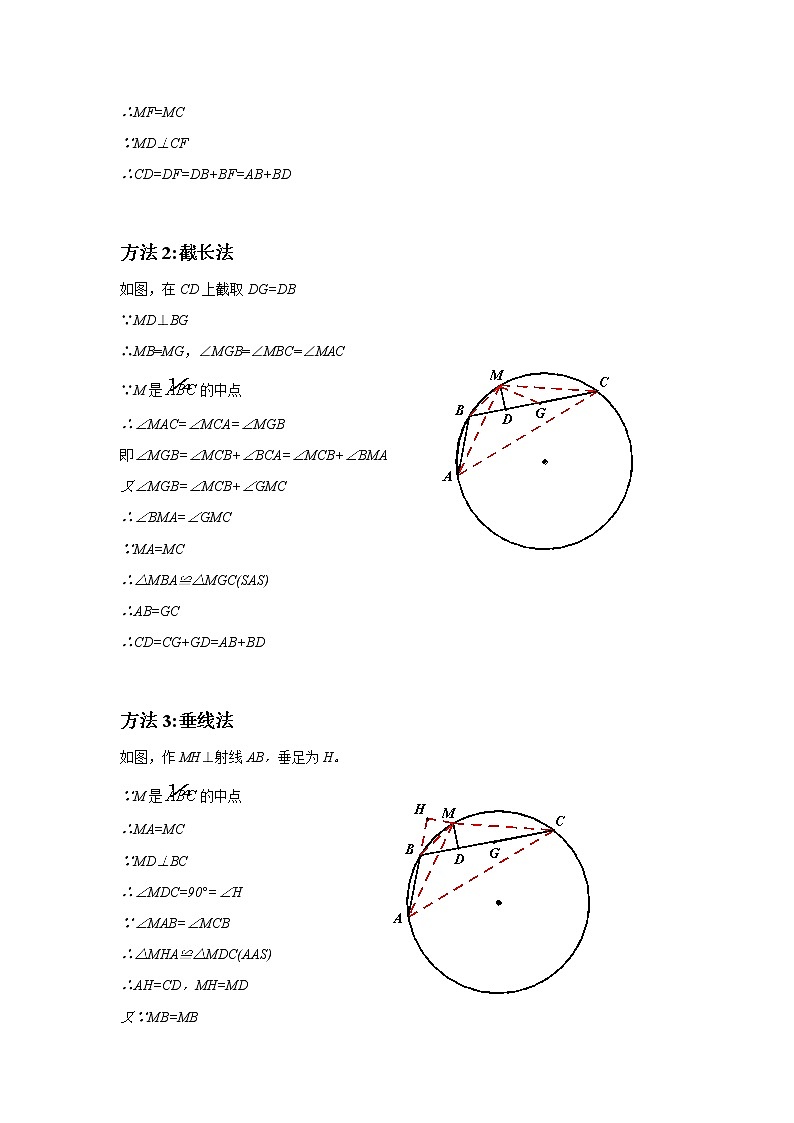
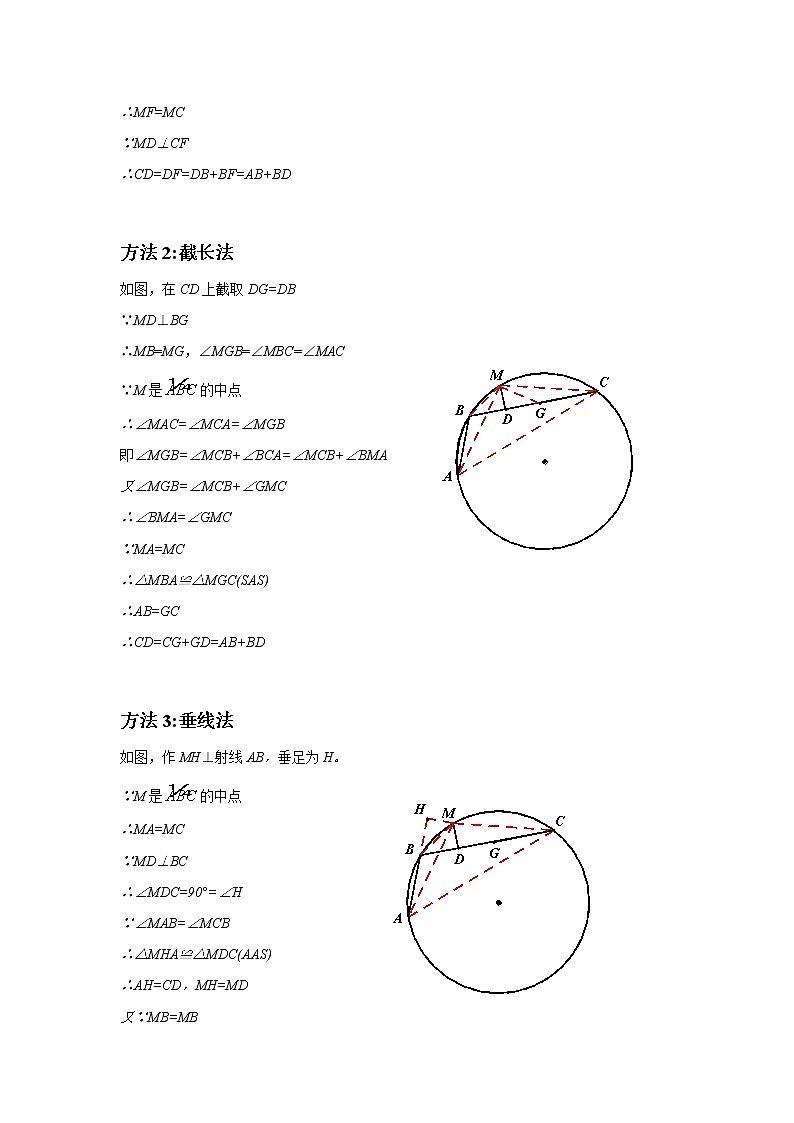
方法2:截长法

如图，在CD上截取DG=DB

∵MD⊥BG

∴MB=MG，∠MGB=∠MBC=∠MAC

∵M是的中点

∴∠MAC=∠MCA=∠MGB

即∠MGB=∠MCB+∠BCA=∠MCB+∠BMA

又∠MGB=∠MCB+∠GMC

∴∠BMA=∠GMC

∵MA=MC

∴△MBA≌△MGC(SAS)

∴AB=GC

∴CD=CG+GD=AB+BD

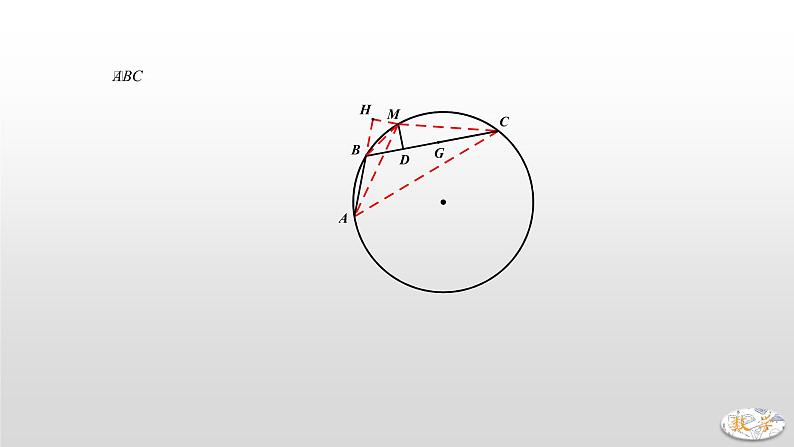
方法3:垂线法

如图，作MH⊥射线AB，垂足为H。

∵M是的中点

∴MA=MC

∵MD⊥BC

∴∠MDC=90°=∠H

∵∠MAB=∠MCB

∴△MHA≌△MDC(AAS)

∴AH=CD，MH=MD

又∵MB=MB

∴Rt△MHB≌Rt△MDB(HL)

∴HB=BD

∴CD=AH=AB+BH=AB+BD

二、典例精析

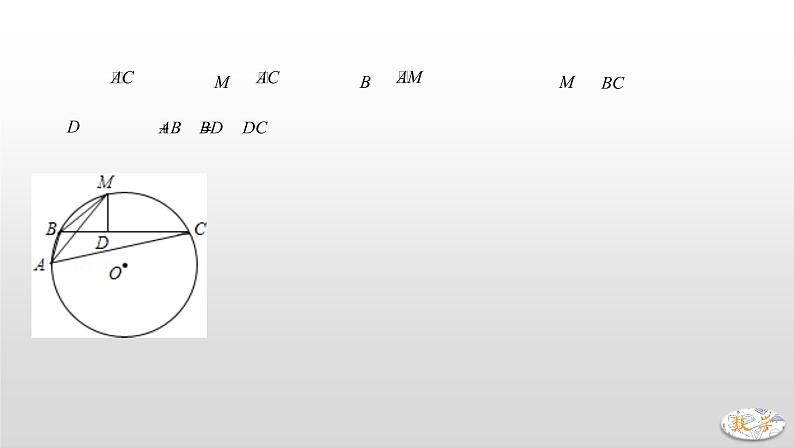
1．如图，是劣弧，是的中点，为上任意一点．自向弦引垂线，垂足为，求证：．

【解答】证明：在上取点，使，连接，

是的中点，

，

（等弧对等弦），

又，

在和中，

，

，

，

为等腰三角形为底），

又，

为中点（等腰三角形三线合一），

．

2．如图所示，在中，，，点为劣弧上的动点，且．

（1）求的长度；

（2）求的值；

（3）过点作，求证：．

【解答】解：（1）作，

，，，

，

，

在中，，

；

（2）连接，

，

，

四边形内接于圆，

，

，

，

公共角，

，

，

；

（3）证明：在上取一点，使得，

与所对的弧是，

，

在和中，，

，

，

，，

，

，，

．

3．小明学习了垂径定理，做了下面的探究，请根据题目要求帮小明完成探究．

（1）更换定理的题设和结论可以得到许多真命题．如图1，在中，是劣弧的中点，直线于点，则．请证明此结论；

（2）从圆上任意一点出发的两条弦所组成的折线，成为该圆的一条折弦．如图2，，组成的一条折弦．是劣弧的中点，直线于点，则．可以通过延长、相交于点，再连接证明结论成立．请写出证明过程；

（3）如图3，．组成的一条折弦，若是优弧的中点，直线于点，则，与之间存在怎样的数量关系？写出结论，不必证明．

【解答】证明：（1）如图1，连接，，

是劣弧的中点，

，

，

，

，，

，

为等腰三角形，

，

；

（2）如图2，延长、相交于点，再连接，

是圆内接四边形，

，

是劣弧的中点，

，

，

为等腰三角形，

，，

，

，

（3）．

连接，，，、相交于点，

弧弧，

，

，

，，

，

，

，，

，

，，

，

，

．

4．已知、、、是上的四点，，是四边形的对角线

（1）如图1，连接，若，求证：是的平分线；

（2）如图2，过点作，垂足为，若，，求线段的长度．

【解答】（1）证明：，

，

，

是等边三角形，

，

，即是的平分线；

（2）解：连接，在线段上取点，使得，连接，

，

，

，

，

，，

，

四边形是圆的内接四边形，

，

，

，

在和中，

，

，

，，

．

5．如图，内接于，，，点为上的动点，且．

（1）求的长度；

（2）在点的运动过程中，弦的延长线交延长线于点，问的值是否变化？若不变，请求出的值；若变化，请说明理由；

（3）在点的运动过程中，过点作，求证：．

【解答】解：（1）作，

，，，

，

，

在中，，

；

（2）连接，

，

，

四边形内接于圆，

，

，

，

公共角，

，

，

；

（3）在上取一点，使得，

在和中

，

，

，

，，

，

，，

．

三、巩固练习

1．先阅读命题及证明思路，再解答下列问题．

命题：如图1，在正方形中，已知：，角的两边、分别与、相交于点、，连接．求证：．

证明思路：

如图2，将绕点逆时针旋转至．，，与重合．，，点、、是一条直线．

根据，得证，得．

（1）特例应用

如图1，命题中，如果，，求正方形的边长．

（2）类比变式

如图3，在正方形中，已知，角的两边、分别与、的延长线相交于点、，连接．写出、、之间的关系式，并证明你的结论．

（3）拓展深入

如图4，在中，、是的弦，且，、是上的两点，．

①如图5，连接、，求证：，；

②若点在（点不与点、、、重合）上，连接、分别交线段、或其延长线于点、，直接写出、、之间的等式关系．

【解答】解：（1）如图1，

设正方形的边长为，则有，．

由材料可知：．

在中，

，

．

．

解得：，（舍去）

所以正方形的边长为6．

（2）．

理由如下：

在上取一点，使得．连接，如图3．

四边形是正方形，

，．

．

在和中，

．

．

，．

．

，

．

在△和中，

．

△．

．

．

（3）①延长到点，使得，连接，如图5．

，，

．

在和中，

．

．

．

．

，

．

．

，，

，．

，．

②Ⅰ．当点在上时，如图6、7．

同理可得：．

Ⅱ．当点在上时，如图8．

同理可得：．

2．问题提出

如图①，、是的两条弦，，是的中点，垂足为，求证：．

小敏在解答此题时，利用了“补短法”进行证明，她的方法如下：

如图②，延长至，使，连接、、、、．

（请你在下面的空白处完成小敏的证明过程．

推广运用

如图③，等边内接于，，是上一点，，，垂足为，则的周长是　　．

拓展研究

如图④，若将“问题提出”中“是的中点”改成“是的中点”，其余条件不变，“”这一结论还成立吗？若成立，请说明理由；若不成立，写出、、三者之间存在的关系并说明理由．

【解答】问题提出：证明：如图2，延长至，使，连接、、、、，

是的中点，

，，

，

，

，

在和中

，

，

，

又，

，

；

推广运用：解：如图3，截取，连接，，，

由题意可得：，，

在和中

，

，

，

，

，则，

，

，

则的周长是，

故答案为：；

拓展研究：不成立，、、三者之间的关系：，

证明：连接，，，交于，

是的中点，

，

在和中，，

，，

，，

，

，

．

3．在中，顺次连接、、．

（1）如图1，若点是的中点，且交延长线于点，求证：为的切线；

（2）如图2，在（1）的条件下，连接，过点作于点，若，，，则、、有何数量关系？

（3）如图3，当时，是延长线上一点，是线段上一点，且，若，的周长为9，请求出的值？

【解答】解：（1）如图1，连接，

是的中点，

，

，

，

为的半径，

为的切线；

（2）如图2，连接交于，连结，

是的中点，

，

，

，

，

，

，

，

是的中点，

，

，

，，

，

，

，

，

，

，

，

，

，

；

（3）过点作，过点作，与交于点，连接，

则，，

是等边三角形，

，，

，，

，，

，

，，

，，

四边形是平行四边形，

，，

，，

，，

过点作于点，交于点，连接，

则，，

，

是等边三角形，

，

，即与在同一直线上，

四边形是平行四边形，

，，

设，则，，，，

，

，即，

，

，

在中，，

，

，

延长，交于点，则，，，

，

，

，

，

，

，

，

，

解得：（舍去），，

，，

作于点，则，

．

4．【问题呈现】阿基米德折弦定理：阿基米德，公元前公元前212年，古希腊）是有史以来最伟大的数学家之一，他与牛顿、高斯并称为三大数学王子．如图1，和是的两条弦（即折线是圆的一条折弦），，点是的中点，则从向所作垂线的垂足是折弦的中点，即．下面是运用“截长法”证明的部分证明过程．

证明：如图2，在上截取，连接、、和．

是的中点，

，

又，，

，

，

又，

，

即．

【理解运用】如图1，、是的两条弦，，，点是的中点，于点，则　　；

【变式探究】如图3，若点是的中点，【问题呈现】中的其他条件不变，判断、、之间存在怎样的数量关系？并加以证明．

【实践应用】如图4，是的直径，点圆上一定点，点圆上一动点，且满足，若，的半径为5，则　　．

【解答】解：【理解运用】：由题意可得，即，

，

，

，

故答案为：1；

【变式探究】．

证明：在上截取，连接、、、，

是弧的中点，

，，

又，

，

，

，

又，

，

，即；

【实践应用】

如图，当点在下方时，过点作于点，

是圆的直径，

，

，圆的半径为5，

，

，

，

，

．

当点在上方时，，同理易得．

综上所述：的长为或，

故答案为或．

5．古希腊数学家阿基米德提出并证明了“折弦定理”．如图1，和是的两条弦（即折线是圆的一条折弦），，是优弧的中点，则从向所作垂线的垂足是折弦的中点，即．

（1）请按照下面的证明思路，写出该证明的剩余部分；

证明：如图2，在上截取，

连接，，和．

是的中点，

，

．

（2）如图（3），已知等边内接于，，为上一点，，，垂足为，请你运用“折弦定理”求的周长．

【解答】（1）证明：如图2，在上截取，

连接，，和．

是的中点，

，

．

在和中

，

，

，

又，

，

；

（2）解：如图3，截取，连接，，，

由题意可得：，，

在和中

，

，

，

，

，则，

，

，

则的周长是．