








专题17【精品】 动圆相切问题-2022年中考数学几何模型解题策略研究(课件+讲义)
展开专题17 动圆相切问题
一、圆心为动点
解题思路:确定圆心到直线的距离d=r即可.
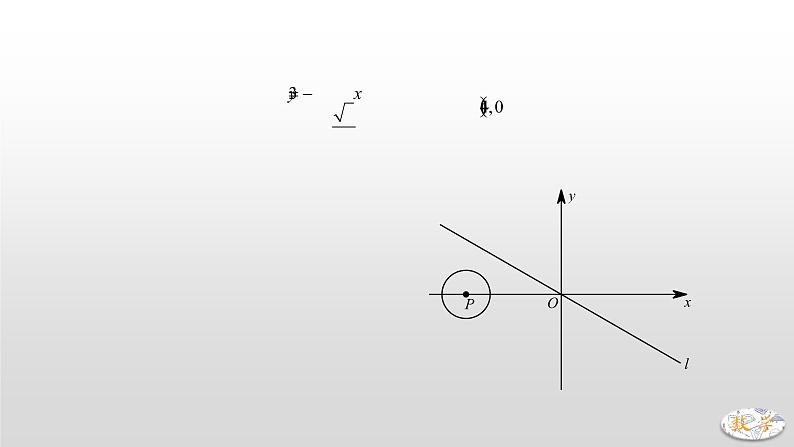
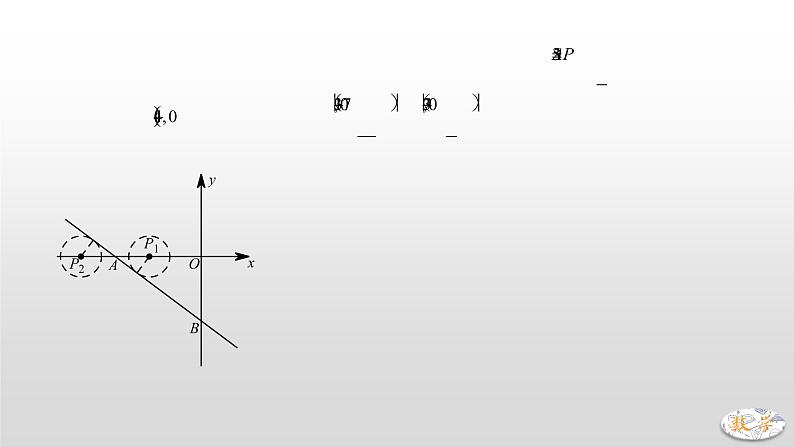
【引例】如图,直线l的解析式为,点P坐标为,以点P为圆心,1为半径作圆,当点P以每秒2个单位的速度向右移动时,时间t为何值时圆P与直线l相切?
【分析】过点P作PH⊥直线l,垂足为H点,当PH=r=1时,即可得圆P与直线l相切.
当点P坐标为或时,PH=1,,,
综上所述,t的值为1或3.
1. (2017·百色)以坐标原点为圆心,作半径为2的圆,若直线与相交,则的取值范围是
A. B. C. D.
【分析】确定两个相切的时刻,当时,直线与圆相切,故若直线与圆相交,则b的取值范围是,故选D.
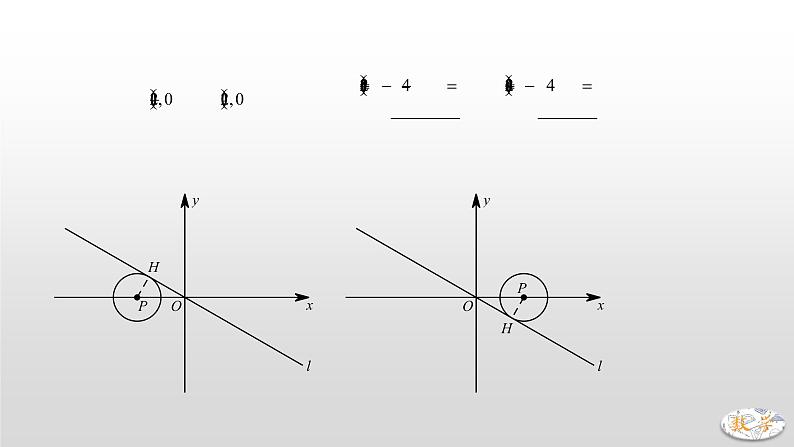
2. (2015·烟台)如图,直线与坐标轴交于,两点,点是轴上一动点,以点为圆心,2个单位长度为半径作,当与直线相切时,则的值为 .
【分析】点M到直线l的距离为2,即可得圆M与直线l相切.
过点M作MH⊥AB交AB于H点,当圆M与直线l相切时,MH=r=2,
,∴BH=4,,
M点在B点左侧时,点M坐标为,
M点在B点右侧时,点M坐标为,
综上,M点坐标为或.
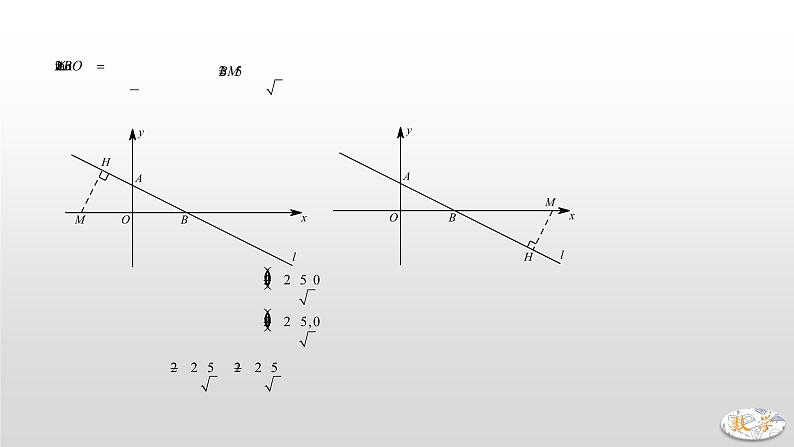
3. (2019·菏泽)如图,直线交轴于点,交轴于点,点是轴上一动点,以点为圆心,以1个单位长度为半径作,当与直线相切时,点的坐标是 .
【分析】若圆P与AB相切,则点P到直线AB的距离为1,可得,
又点A坐标为,故点P坐标为或.
4. (2016·无锡)如图,中,,,,点从点出发,在边上以的速度向点运动,与此同时,点从点出发,在边上以的速度向点运动,过的中点作的垂线,则当点运动了 时,以点为圆心,为半径的圆与直线相切.
【分析】易证CD∥AB,当圆C与直线EF相切时,,,
,,∴,
5. (2019·宁波)如图,Rt△ABC中,,,点在边上,,.点是线段上一动点,当半径为6的与的一边相切时,的长为 .
【分析】当圆P与BC边相切时,过点P作PH⊥BC交BC,则PH=6,
易证△DHP∽△DCA,,解得:,∴.
当圆P与AB边相切时,过点P作PM⊥AB交AB于M点,则PM=6,
过点D作DN⊥AB交AB于点N,易证△BND∽△BCA,可得:,解得:,
易证△AMP∽△AND,,解得:.
综上,AP的长为或.
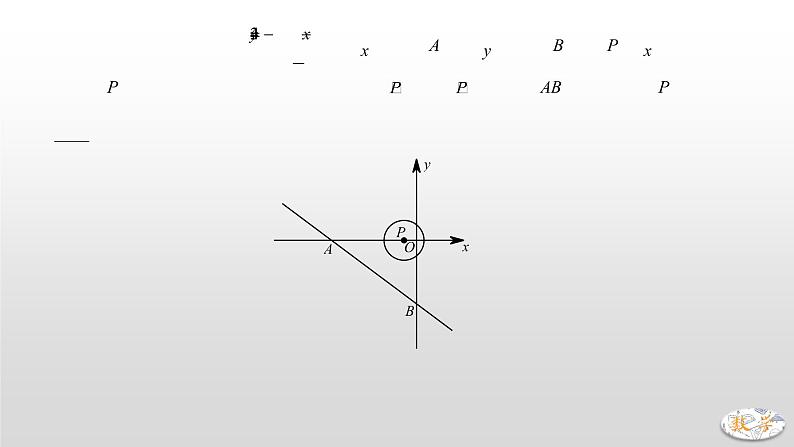
6. 如图,点的坐标是,点是以为直径的上一动点,点关于点的对称点为.当点在上运动时,所有这样的点组成的图形与直线有且只有一个公共点,则的值等于 .
【分析】确定点P轨迹,考虑AP=2AC始终成立,可得点P轨迹是以点O为圆心,OA为半径的圆,若圆与直线相切,则半径等于点O到直线的距离,用面积法可求,故,则.
【动圆相切-与多边形相切】
(2018·宁波)如图,正方形的边长为8,是的中点,是边上的动点,连结,以点为圆心,长为半径作.当与正方形的边相切时,的长为 .
【分析】圆不可能与AB、BC边相切.
当圆P与CD相切时,即PM=PC
如图所示,设BP=x,则,,
则,解得:x=3.
当圆P与AD相切时,即PM=r=8,
解得.
综上,BP的长为3或.
7. (2015·连云港)已知如图:在平面直角坐标系中,直线与轴、轴分别交于、两点,是直线上一动点,的半径为1.
(1)判断原点与的位置关系,并说明理由;
(2)当过点时,求被轴所截得的劣弧的长;
(3)当与轴相切时,求出切点的坐标.
【分析】
(1)过点O作OH⊥AB于点H,可得,∴,
故点O在圆外.
(2)记圆P与y轴另外一交点为C,连接PC,则∠BPC=120°,
则,故圆P被y轴截得的弧长为.
(3)圆P与x轴相切,即点P到x轴距离为1即可,,
当时,,解得:,
当时,,解得:,
故切点的坐标为或.
8. (2016·苏州)如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,0.8cm为半径作圆O,点P与点O同时出发, 设它们的运动时间为t(单位:s)().
(1) 如图1,连接DQ平分∠BDC时,t的值为 ;
(2) 如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3) 请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与圆O相切时,求t的值;并判断此时PM与圆O是否也相切?说明理由 .
【分析】
(1)由题意得:PB=4t,PQ=3t,BQ=5t,CQ=8-5t,
若DQ平分∠BDC,则CQ=PQ,即8-5t=3t,解得:t=1,
故t的值为1;
(2)过点M作MH⊥BC交BC边于点H,
若△CMQ是以CQ为底的等腰三角形,则H为CQ中点,
则,,
易证,代入得:,解得:,故t的值为.
(3)①由于点O与直线MQ均为运动的,可取对角线BD为参照物.
过点O作OE⊥BD交BD于点E,则OD=3t,,
又,∴,
∴点O始终在QM所在直线的左侧.
②过点O作FG⊥BD交BD于点F,则FG⊥MQ,垂足记为G,
若圆O与四边形相切,则,解得:,
即当s时,圆与QM相切,
此时若圆O与MP也相切,则MO平分∠PMQ,即,
,又,∴,,
∴,又OG=r=0.8cm,
∴,
∴此时PM与圆O不相切.
二、动点为直径
解题思路:由切线的性质-垂直于过切点的半径,得垂直关系,再由三角函数值求得线段长.
【引例】在矩形ABCD中,AB=4,BC=3,连接BD,点P从D点出发以每秒1个单位向点C运动,点Q从点B出发以每秒2个单位向点D运动,以PQ中点O为圆心,PQ为直径作圆,运动时间t为何值时,圆O与BD相切?
【分析】当PQ⊥BD时,圆O与BD相切,
由题意得:DP=t,DQ=5-2t,若PA⊥BD,即,
代入得:,解得:,
故当t的值为时,圆O与BD相切.
【与多边形边相切,三角函数解线段关系】
1.(2018·相城区一模)如图,在Rt△ABC中,,,,动点从点出发,在边上以每秒的速度向点匀速运动,同时动点也从点出发,沿以每秒的速度匀速运动,运动时间为秒,连接,以为直径作.
(1)当时,求的面积;
(2)设的面积为,求与的函数关系式;
(3)当点在上运动时,与Rt△ABC的一边相切,求的值.
【分析】当时,cm,cm,∴cm².
(2)当时,,
∴,,;
当时,
,,
∴
,
∴
(3)当点Q在AB上时,,
当圆O与BC边相切时,即PQ⊥BC,
,,,
代入得:, 解得:t=1;
当圆O与AB相切时,即PQ⊥AB,
,代入得:,解得:;
当圆O与AC边相切时,过点O作ON⊥AC交AC于点N,则,
,
,
由得:,
解得:,(舍).
故综上所述,t的值为1或或.
三、交点个数的分析
圆与线段或图形交点个数问题,考虑交点个数变化的位置,当①圆与线段相切、②圆过线段端点时,交点个数会发生改变.
【引例】如图,在坐标系中,点A坐标为(1,0),点B坐标为(0,3),以点P(m,0)(m<0)为圆心,4为半径作圆,m为何值时,圆P与线段AB只有1个交点?
【分析】
考虑圆P与AB相切:过点P作PH⊥AB,当PH=4时,圆P与AB相切,
易证△PHA∽△BOA,∴,此时;
当圆P过点A时,m=-3;
当圆P过点B时,,故;
综上,当或时,圆P与线段AB只有1个交点.
1.(2017·吴中区一模)如图,在矩形中,,,动点从点出发,沿着方向以1个单位长度秒的速度匀速运动,同时动点从点出发,沿着对角线方向也以1个单位长度秒的速度匀速运动,设运动时间为秒,以为圆心,长为半径的与、的另一个交点分别为、,连结、.
(1)填空: (用的代数式表示);
(2)当为何值时,点与点相遇?
(3)当线段与有两个公共点时,求的取值范围.
【分析】
(1)BE=2t,.
(2),若点Q与点F相遇,则AQ+BF=6,
即,解得:,
故t为时,点Q与点F相遇.
(3)考虑何时QE与圆P相切,即当QE⊥BD时,
,又,BE=2t,代入得:,
解得:.
从相切开始,至点Q与点F重合,有2个交点,
故t的取值范围是.
2.(2013·连云港)如图,在平面直角坐标系中,为坐标原点,点、的坐标分别为、.动点从点、动点从点同时出发,分别沿着方向、方向均以1个单位长度秒的速度匀速运动,运动时间为(秒.以为圆心,长为半径的与、的另一个交点分别为、,连接、.
(1)求当为何值时,点与点重合?
(2)设的面积为,试求与之间的函数关系式,并求的最大值;
(3)若与线段只有一个交点,请直接写出的取值范围.
【分析】
(1),,若点Q与点D重合,
则,即,解得:.
(2)当时,
,,
,
当时,
则,∴,
综上,.
当t=5时,S的最大值为15.
(3)1个交点:在CQ与圆P相切及之前,在Q、D相遇之后,
OQ=t,AC=2t,,,解得:,
故当或时,圆P与线段QC只有1个交点.
3.(2019·河北)如图1和2,中,,,.点为延长线上一点,过点作切于点,设.
(1)如图1,为何值时,圆心落在上?若此时交于点,直接指出与的位置关系;
(2)当时,如图2,与交于点,求的度数,并通过计算比较弦与劣弧长度的大小;
(3)当与线段只有一个公共点时,直接写出的取值范围.
【分析】
(1),∴,
∴PC=12,PB=9,∴x的值为9时,点O落在AP上.
此时PE⊥BC,∵PE⊥AD,AD∥BC,∴可得PE⊥BC.
(2)过点C作CH⊥AP交AP于点H,设PH=x,
则,∵,∴,
∴,,
∴AH=3+12=15,∴AH=CH,
∴∠CAP=45°.
过点O作ON⊥AP交AP于点N,则,
易证△PNO∽△CHP,又PH=5,CH=12,∴CP=13,
∴,代入得:,解得:,
,
∵,∴弦AP长度大于弧PQ长度.
(3).
当BP=18时,圆O与DA相切,当BP>18时,圆O与AD边只有一个交点A.
【与多边形交点个数问题】
4.(2018·镇江)如图1,平行四边形中,,,,点在边上运动,以为圆心,为半径的与对角线交于,两点.
(1)如图2,当与边相切于点时,求的长;
(2)不难发现,当与边相切时,与平行四边形的边有三个公共点,随着的变化,与平行四边形的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的的值的取值范围 .
【分析】
(1)连接PF,则PF⊥CD,且PA=PF,设PA=x,则PF=x,PD=10-x,
,解得:,
∴AP的长为.
(2)从圆P与CD边相切开始,有4个交点,直到圆P与BC边相切于点M,
此时PM⊥BC,易求,∴.
之后交点个数大于4,直到如下图,圆P过点D,则过点C,且与BC边有1交点,
此时PA=PD=.
综上所述,公共点个数为4时, 或.
5.(2012·无锡)如图,菱形的边长为,.点从点出发,以的速度,沿向作匀速运动;与此同时,点也从点出发,以的速度,沿射线作匀速运动.当运动到点时,、都停止运动.设点运动的时间为.
(1)当异于、时,请说明;
(2)以为圆心、长为半径作圆,请问:在整个运动过程中,为怎样的值时,与边分别有1个公共点和2个公共点?
【分析】
(1)由题意得:cm,cm,
AB=2cm,cm,∴,
∴△APQ∽△ACB,∴∠APQ=∠ACB,∴PQ∥BC.
(2)当圆P与BC相切时,有1个公共点,
AQ=t,PH=PQ=AQ=t,,,
,∴s;
当圆P过点B时,圆P与BC边有2个交点,
此时△PBQ是等边三角形,点P为AC中点,∴cm,t=1s;
当圆P过点C时,,解得:,
∴,则;
当点P与点C重合时,圆P与BC边有1个交点,此时t=2;
当或或t=2时,圆P与BC边有1个交点;
当时,圆P与BC有2个交点.
四、构造相切求最值
【线段最值】
1.(2011·河池)如图,在Rt△ABC中,是直角,,,是边上的动点,设,若能在边上找到一点,使,则的取值范围是 .
【分析】点Q满足∠BQP=90°,则以BP为直径作圆,与AC边交点即为点Q,存在这样的点Q即圆与AC有交点.求x的取值范围即分别确定BP的最大值和最小值.
当圆与AC相切时,BP最小,
圆心记为点O,连接OQ,则OQ=OB,由,得,
∴,∴,,
当点P与点C重合时,BP最大,最大值为4,
故x的取值范围是.
【米勒问题-相切构造最大角】
2.如图,在平面直角坐标系中,A(1,0)、B(5,0)直线l经过点C(-1,2),点P是直线l上的动点,若∠APB的最大值为45°,求直线l的解析式.
【分析】
考虑到直线l未知但∠APB的最大值已知为45°,故构造圆.
记△ABP外接圆圆心为M点,则∠AMB=2∠APB=90°,
故可确定M点位置.
根据A(1,0)、B(5,0),不难求得M点坐标为(3,2),
连接MC、MP,考虑到圆M与直线CP相切,故MP⊥CP,△CPM是直角三角形.
∵MC=4,MP=MA=,
∴,即△CPM是等腰直角三角形,
易求P点坐标为(1,4),
又C点坐标为(-1,2),
可求直线l的解析式为y=x+3.
专题24【精品】 圆内最大张角米勒角问题-2022年中考数学几何模型解题策略研究(课件+讲义): 这是一份专题24【精品】 圆内最大张角米勒角问题-2022年中考数学几何模型解题策略研究(课件+讲义),文件包含专题24圆内最大张角米勒角问题pptx、专题24圆内最大张角米勒角问题解析版docx、专题24圆内最大张角米勒角问题原卷版docx等3份课件配套教学资源,其中PPT共14页, 欢迎下载使用。
专题14【精品】 圆之切线的判定-2022年中考数学几何模型解题策略研究(课件+讲义): 这是一份专题14【精品】 圆之切线的判定-2022年中考数学几何模型解题策略研究(课件+讲义),文件包含专题14圆之切线的判定pptx、专题14圆之切线的判定解析版docx、专题14圆之切线的判定原卷版docx等3份课件配套教学资源,其中PPT共38页, 欢迎下载使用。
专题12 【精品】圆(基础知识)-2022年中考数学几何模型解题策略研究(课件+讲义): 这是一份专题12 【精品】圆(基础知识)-2022年中考数学几何模型解题策略研究(课件+讲义)












