


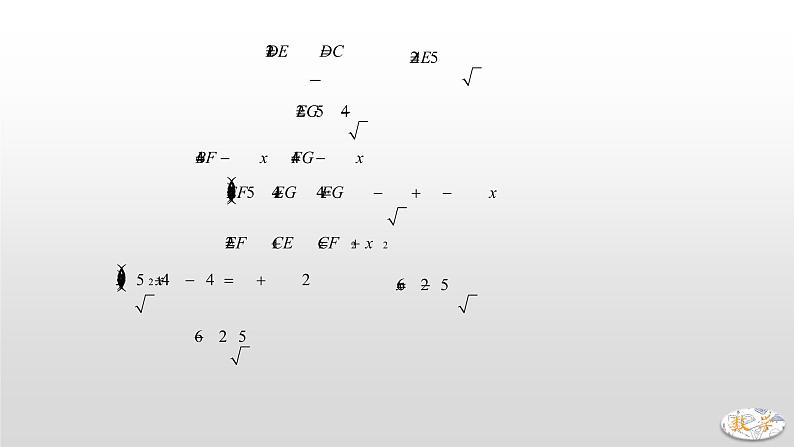




所属成套资源:精品2022年中考数学几何模型解题策略研究(课件+讲义)
专题09【精品】 正方形中的对称、折叠问题-2022年中考数学几何模型解题策略研究(课件+讲义)
展开
这是一份专题09【精品】 正方形中的对称、折叠问题-2022年中考数学几何模型解题策略研究(课件+讲义),文件包含专题09正方形中的对称折叠问题pptx、专题09正方形中的对称折叠问题解析版doc、专题09正方形中的对称折叠问题原卷版doc等3份课件配套教学资源,其中PPT共24页, 欢迎下载使用。
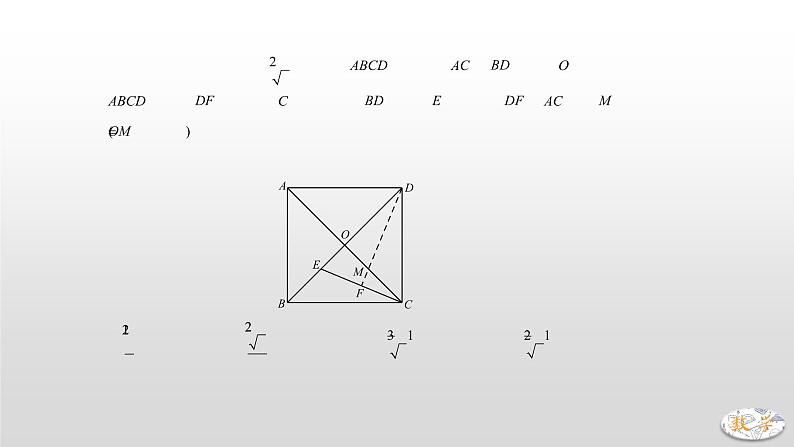
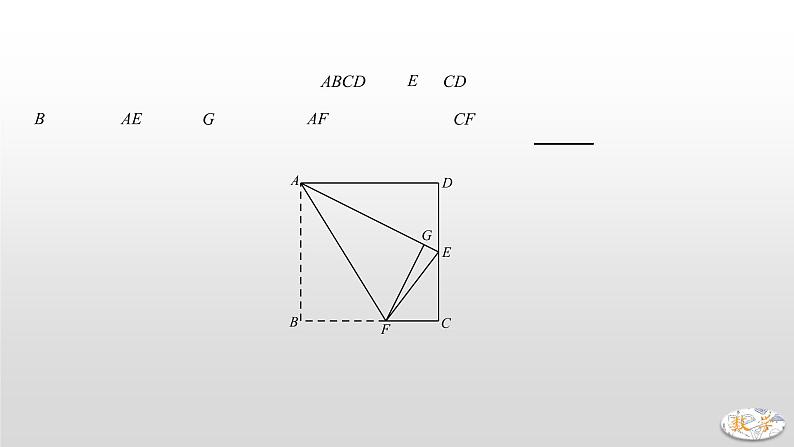
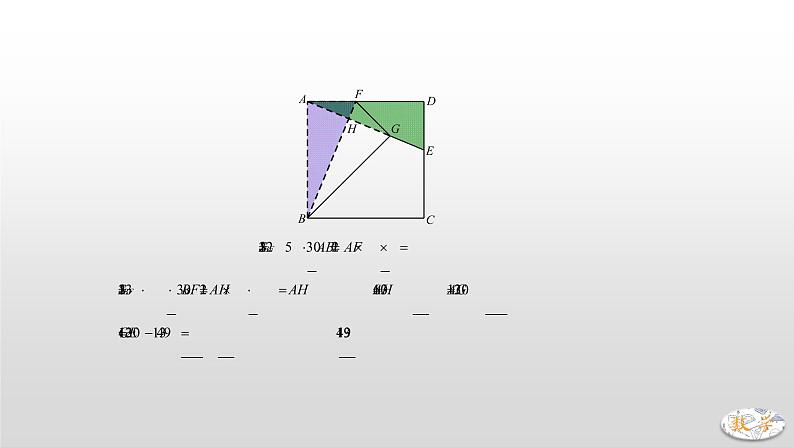
专题09 正方形中的对称、折叠问题正方形既是轴对称图形,也是中心对称图形,关于对称可以考察对称的基本性质,也可以有关于构造对称,而涉及到计算的,无非就是勾股或者三角函数.一、典例精析1.(2019·兰州)如图,边长为的正方形的对角线与交于点,将正方形沿直线折叠,点落在对角线上的点处,折痕交于点,则 A. B. C. D.【分析】由题意可得:DF⊥EC,易证△DOM≌△COE,∴OM=OE=DE-DO=.故选D. 【长度的计算——勾股定理】2.(2019·青岛)如图,在正方形纸片中,是的中点,将正方形纸片折叠,点落在线段上的点处,折痕为.若AD=4,则的长为 . 【分析】∵E点是CD中点,∴,∴,由折叠可知AG=AB=4,∴,设CF=x,则,,在Rt△EFG中,,在Rt△CEF中,,∴,解得:.∴CF的长为.【对称性质——对称点连线被对称轴垂直且平分】3.(2019·天津)如图,正方形纸片的边长为12,是边上一点,连接、折叠该纸片,使点落在上的点,并使折痕经过点,得到折痕,点在上,若,则的长为 .【分析】易证△ADE≌△BAF,∴AF=DE=5,BF=13,记AE与BF交点为H,,又,∴,,∴.故GE的长为.
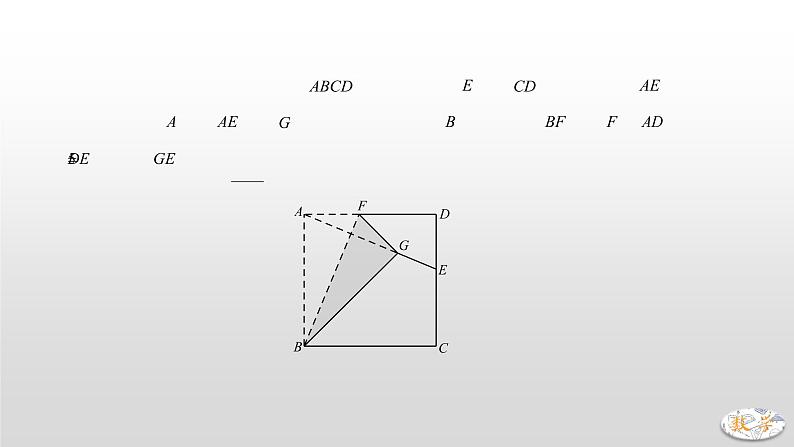
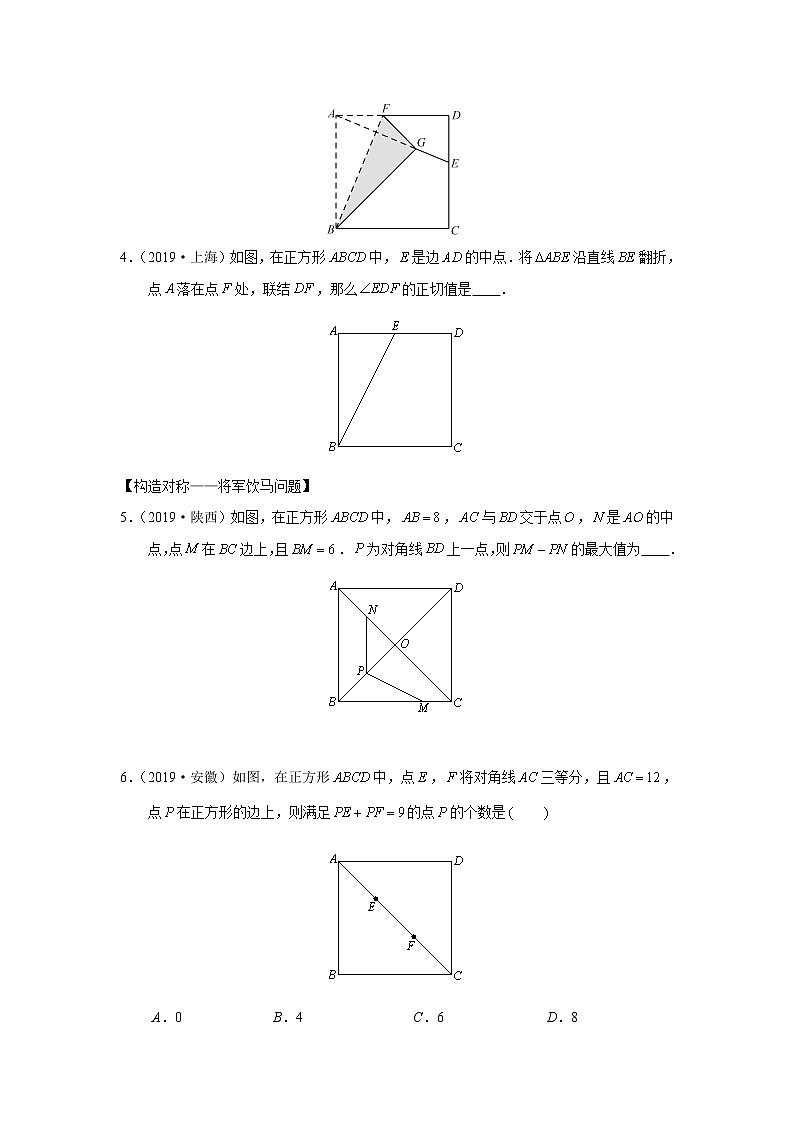
4.(2019·上海)如图,在正方形中,是边的中点.将沿直线翻折,点落在点处,联结,那么的正切值是 .【分析】如图,点F如图所示,连接BF、DF、EF、AF,记AF与BE交点为H,由对称可知AF⊥BE,点H是AF中点,又点E是AD中点,∴EH是△DF边所对的中位线,∴EH∥DF,∴∠EDF=∠AEB,∴tan∠EDF=tan∠AEB=2. 【构造对称——将军饮马问题】5.(2019·陕西)如图,在正方形中,,与交于点,是的中点,点在边上,且.为对角线上一点,则的最大值为 .【分析】作点M关于BD的对称点,根据对称性可知在AB上且,连接,则,∴,当、N、P共线时,此时,取到最大值.∵,∴∽△ABC,即是等腰直角三角形,∴,故PM-PN的最大值为2. 6.(2019·安徽)如图,在正方形中,点,将对角线三等分,且,点在正方形的边上,则满足的点的个数是 A.0 B.4 C.6 D.8【分析】可以先考虑一边上点P的数量,再由对称性得所有点P的个数.考虑在AD上任取一点P,所得PE+PF的最小值和最大值.先求PE+PF最小值:作点E关于直线AD的对称点,连接、,则PE+PF=,当、P、F共线时,取到最小值,此时,显然>9,∴在AD上存在两个点P使得PE+PF=9,在正方形的边上有8个这样的点P,故本题选D.二、中考真题演练1.(2020•资阳)如图,在边长为4的正方形中,点是边上的一点,将沿翻折得到,连接,使,则的长是 A.1 B. C. D. 解:过点作于点,并延长交于点,,,设,则,,将沿翻折得到,,,,,,,,,,,,,,.故选:.2.(2021•牡丹江)如图,正方形的边长为3,为边上一点,.将正方形沿折叠,使点恰好与点重合,连接,,,则四边形的面积为 A. B. C.6 D.5 解:设,,正方形的边长为3,,,由折叠可得,,,在中,,即,在中,,,,,,,在中,,,,,,,,故选:.3.(2020•广东)如图,在正方形中,,点,分别在边,上,.若将四边形沿折叠,点恰好落在边上,则的长度为 A.1 B. C. D.2 解:四边形是正方形,,,,将四边形沿折叠,点恰好落在边上,,,,,设,则,,,解得.故选:.4.(2021•东营)如图,正方形纸片的边长为12,点是上一点,将沿折叠,点落在点处,连接并延长交于点.若,则的长为 . 解:设与交于点,将沿折叠,点落在点处,,,四边形是正方形,,,,,在和中,,,,,,,,,,,故答案为:.5.如图,边长为1的正方形中,点为的中点.连接,将沿折叠得到,交于点,求的长. 解:延长交于,连接.四边形是正方形,,,,,由翻折的性质可知,,,,点是的中点,,,在和中,,,,,,,,,,,,,,,.
相关课件
这是一份专题02【精品】 半角模型-2022年中考数学几何模型解题策略研究(课件+讲义),文件包含专题02半角模型pptx、专题02半角模型解析版doc、专题02半角模型原卷版doc等3份课件配套教学资源,其中PPT共37页, 欢迎下载使用。
这是一份专题20【精品】 最值之胡不归问题-2022年中考数学几何模型解题策略研究(课件+讲义),文件包含专题20最值之胡不归问题pptx、专题20最值之胡不归问题解析版docx、专题20最值之胡不归问题原卷版docx等3份课件配套教学资源,其中PPT共31页, 欢迎下载使用。
这是一份专题10【精品】 将军饮马模型(一)对称问题-2022年中考数学几何模型解题策略研究(课件+讲义),文件包含专题10将军饮马模型一对称问题pptx、专题10将军饮马模型一对称问题解析版doc、专题10将军饮马模型一对称问题原卷版doc等3份课件配套教学资源,其中PPT共24页, 欢迎下载使用。










