安徽省合肥市瑶海区第三十中学2021-2022学年中考二模数学试卷

这是一份安徽省合肥市瑶海区第三十中学2021-2022学年中考二模数学试卷，文件包含安徽省合肥市瑶海区三十中2021-2022学年中考二模数学试卷解析版docx、安徽省合肥市瑶海区三十中2021-2022学年中考二模数学试卷原卷docx等2份试卷配套教学资源，其中试卷共14页， 欢迎下载使用。

一、选择题（本大题共10小题，每小题4分，满分40分）
1、在－2，，－1，－3这四个数中，比大的数是( )
A. －2 B. C. －1 D. －3
【答案】B
【解析】∵-3＜-2＜-1＜-＜-，∴B正确，A、C、D错误；
故选B
2、《安徽省2021年国民经济和社会发展统计公报》显示，2021年安徽省全年邮政行业业务总量393.6亿元。将
393.6亿用科学记数法表示为（ ）
×109 ×1010 C.0. 3936×1010 ×1011
【答案】B
【解析】∵393.6亿=39 360 000 000=3.936×1010，∴B正确,， A、C、D错误；
故选B
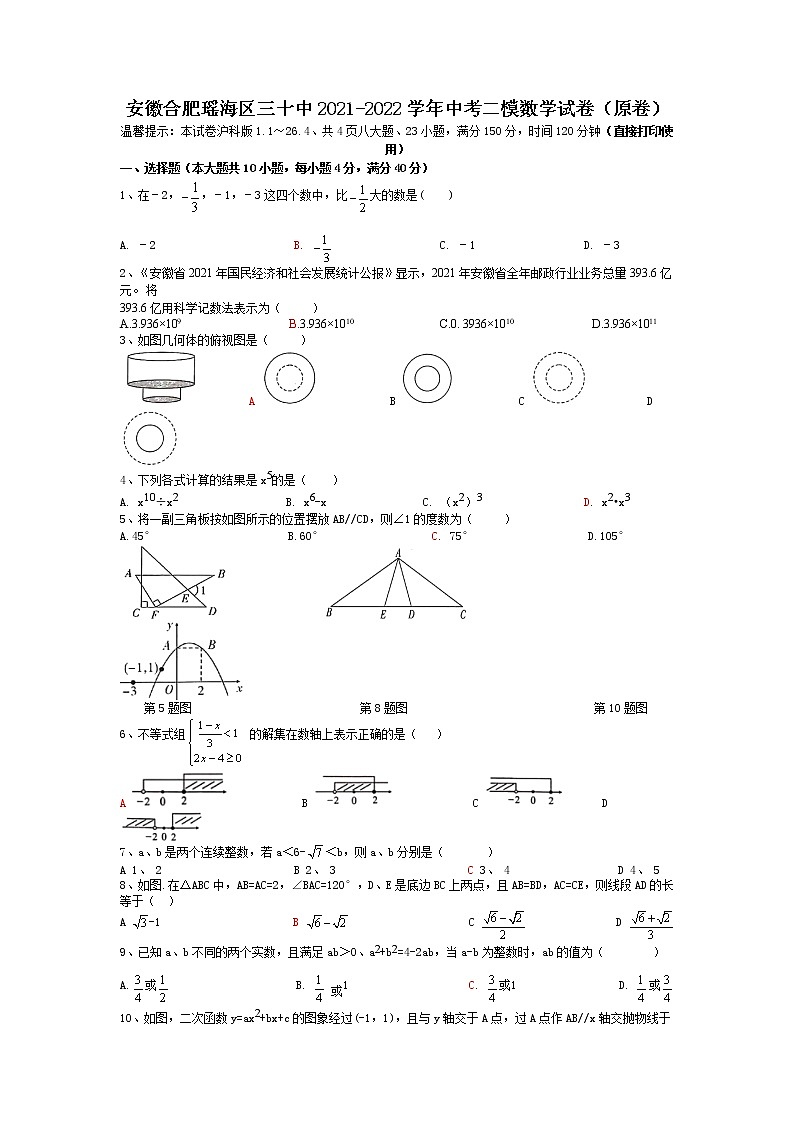
3、如图几何体的俯视图是（ ）
A B C D
【答案】A
【解析】从上往下看，可以看到一个实线圆和在实线圆内并与实线圆同一圆心的虚线圆，A正确，B、C、D错误；
故选A
4、下列各式计算的结果是x的是（ ）
A. x÷x B. x-x C. （x） D. x•x
【答案】D
【解析】A. x÷x =x； B. x与x不属于同类项，不能合并； C. （x） =x6 ； D. x•x=x
故选D
5、将一副三角板按如图所示的位置摆放AB//CD，则∠1的度数为（ ）
A.45° B.60° C. 75° D.105°
【答案】C
【解析】如图所示：∵AB//CD，∴∠1=∠B+∠D=30°+45°=75°；
故选C
6、不等式组 的解集在数轴上表示正确的是（ ）
A B C D
【答案】A
【解析】 ，解不等式组 = 1 \* GB3 ①得：x＞-2；解不等式组 = 2 \* GB3 ②得x≥2，∴原不等式组的解集为x≥2；
故选A
7、a、b是两个连续整数，若a＜6-＜b，则a、b分别是（ ）
A 1、 2 B 2、 3 C 3、 4 D 4、 5
【答案】C
【解析】∵2＜＜3，∴-3＜-＜-2，3＜6-＜4，∴a=3、b=4；
故选C
8、如图.在△ABC中，AB=AC=2，∠BAC=120°，D、E是底边BC上两点，且AB=BD，AC=CE，则线段AD的长等于（ ）
A -1 B C D
【答案】
【解析】∵AB=BD，AC=CE，AB=AC，∠BAC=120°，∴∠B=∠C=30°，∴△ABD≌△ACE，∴AE=AD。
过点A作AH⊥BC，垂足为H，则EH=DH，AH=1，CH=，BC=2，设DH=EH=x，则4-2x=2，x=2-，
由勾股定理得：AD=
故答案：
9、已知a、b不同的两个实数，且满足ab＞0、a+b=4-2ab QUOTE ??>0 QUOTE ?2+?2=9−2?? ，当a-b QUOTE ?−? 为整数时，ab QUOTE ?? 的值为（ ）
A.或 B. QUOTE 或 或1 C. 或1 D. 或
【答案】C
【解析】∵a+b=4-2ab，∴（a+b）=4，设（a-b）2=a2-2ab+b2=t，则4ab=4-t；∴ab=＞0，
∴4ab＞4-t，又∵a-b为整数，∴t=0、1、2、3；
当t=0时，ab=1，a-b=0，满足题意；
当t=1时，ab=，a-b=±1，满足题意;
当t=2时，ab=， a-b=±，不满足题意；
当t=3时，a-b=±，不满足题意； ab的值为1或
故选C
10、如图，二次函数y=ax+bx+c的图象经过(-1，1)，且与y轴交于A点，过A点作AB//x轴交抛物线于点B，且B点的横坐标为2，结合图象，则a的取值范围是（ ）
A a＜- B -＜a＜0 C a＜- D -＜a＜0
【答案】A
【解析】二次函数y=ax+bx+c的图象经过(-1，1)，即a-b+c=1，∵点B横坐标为2，∴-=1，即b=-2a；
∴c=1-3a，由图像可知：9a-3b+c＜0，∴9a+6a+1-3a＜0，∴a＜-
故选A
二、填空题（本大题共4小题，每小题5分，满分20分）
11、分解因式x-9x=
【答案】x（x+3）（x-3）
【解析】x-9x=x（x+3）（x-3）
故答案：x（x+3）（x-3）
12、如图，正五边形ABCDE边长为1，分别以点C、D为圆心，边CD长为半径画弧，两弧交于点F，则弧BF长为
【答案】
【解析】连接CF、DF，则△CDF为等边三角形，∴CF=1，∠FCD=60°，∵ABCDE为正五边形，∴∠BCD=108°，
∴∠BCF=108°-60°=48°，∴弧BF=
故答案：
13、如图，已知A、B是函数(x＞0)图象上的两点，点B位于点A的左侧，AM、BN均垂直于x轴，垂足为点
M、N，连接AO，交BN于点E，若NE=NB，四边形AMNE的面积为2，则k的值为 .
【答案】6
【解析】如图，连接OB，则S△BOE=S四边形AMNE=2，∵NE=NB，∴S△EON=1，∴S△BON=3，∴k=6.
故答案：6
14、在等边三角形ABC中，AB=6，D、E是BC上的动点，F是AB上的动点，且BF=BD=EC=k，连接FE
（1）当k=2时，S△DEF：S△ABC= ； （2）取EF的中点G ，连接GA、GC，则GA+GC的最小值为
【答案】（1）1：9；（2）
【解析】（1）∵BF=BD=EC=2，∴△BDF为等边三角形，BD=DE=2，S△BDF=S△DEF，
∴S△BDF：S△ABC =（BF：AB）=1：9，∴S△DEF：S△ABC =1：9；
（2）∵AG＞0、CG＞0，∴（-）≥0，∴AG+CG≥2•，要使AG+CG最小，必须=，
即AG=CG，∴点G在线段AC的垂直平分线上，∴BG垂直平分线段AC，延长BG交AC于点H，则GH垂直平分AC，
∴EF//AC，∵DF//AC，∴DF与EF重合，∴BD（E）=CD（E），即EF为△ABC中位线。
在等边△ABC与△BEF中，∵AB=6，BF=3，由勾股定理得：BH=3，BG=，∴GH=，∵AH=3，
由勾股定理得：AG=，∴AG+CG=
故答案：（1）1：9；（2）；
三、(本大题共2小题，每小题8分，总计16分)
15、
【答案】
【分析】二次根式、负指数幂、零指数幂及三角函数的化简，然后进行计算即可解答
【解析】
QUOTE 27−2???60°+(2022−?)0−(12)−2
16、某工厂去年的总产值比总支出多90万元，今年比去年的总产值增加10%，总支出节约20%．如果今年的总产值比总支出多120万，那么去年的总产值和总支出分别是多少万元？
【答案】
【分析】设去年的总产值为x万元，总支出为y万元，根据“去年的总产值比总支出多90万元，今年的总产值比总支出多120万”，即可得出关于x，y的二元一次方程组，解之即可得出结论．
【解析】设去年的总产值为x万元，总支出为y万元，
依题意得：x−y=90(1+10%)x−(1−20%)y=120，解得：x=160y=70．
答：去年的总产值为160万元，总支出为70万元．
四、(本大题共2小题，每小题8分，总计16分)
17、如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A(0，3)、B(3，4)、C(2，2)(正方形网格中每个小正方形的边长为1个单位长度).
（1）画出△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是 ；
（2）以点B为位似中心，在网格中画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2∶1；
（3）求出△A2BC2的面积
【答案】
【分析】（1）直接利用平移的性质得出对应点位置进而得出答案；
（2）直接利用位似图形的性质得出对应点位置进而得出答案；
（3）直接利用等腰直角三角形的性质求出△A2BC2的面积；
【解析】（1）如图所示：△A1B1C1，即为所求；C1（3，-4）；
（2）如图所示：△A2BC1，即为所求；
（3）由图形可得：△A2BC2是等腰 直角三角形，且A2C2=BC2=2，故△A2BC2的面积为：×2×2=10.
18、观察以下等式：第1个等式：； 第2个等式：；
第3个等式：；第4个等式：；……；按照以上规律，解决下列问题：
（1）写出第5个等式：
（2）写出你猜想的第n个等式： (用含n的等式表示)，并证明。
【答案】
【分析】（1）由所给的等式不难求出第5个等式；
（2）分析所给的等式的形式，即可得出第n个等式，再把等式左边进行整理即可求证；
【解析】（1）
（2）
证明：左边=右边，所以原等式成立；
五、(本大题共2小题，每小题10分，总计20分)
19、如图，一航船在A处测得北偏东45°方向上有一个灯塔B，航船向正东方向以10nmile/h的速度航行1.5h到达C处时，又测到灯塔B在北偏东15°方向上。已知以灯塔B为圆心，方圆20nmile内有暗礁，问：航船继续向正东方向航行是否有触礁危险？（参考数据：≈1.732，≈2.449）
【答案】
【分析】过C作CH⊥AB，垂足为H，在直角△ACH中，根据三角函数求得CH的长，再在直角△BCH中运用三角函数求出BH，过点B作BM⊥AC，垂足为点M，根据三角形的面积公式出BM与20nmile比较即可.
【解析】过C作CH⊥AB，垂足为H，在直角△ACH中，AC=10nmile/h×1.5h=15 nmile，∠BAC=45°，
sin∠BAC=，CH=AC•sin∠BAC=15×=（nmile），即BH=（nmile），
在直角△BCH中，∠B=180°-45°-90°-15°=30°，tanB=，∴BH==（nmile）
∴AB=AH+BH=（nmile），在直角△ABM中，sin∠BAM=，
∴BM=AB•sin∠BAM=×=≈20.49（nmile）＞20nmile，
∴没有触礁危险。
20、如图，AB是⊙0的直径，AC⊥AB，D是AC的中点，BC交⊙0于点E。
（1）求证：DE与⊙0相切； （2）若AE=3、DE=2，求⊙O的半径长；
【答案】
【分析】（1）利用直角三角形斜边中线的性质和等腰三角形的性质证明∠DEA+∠OEA =∠BAC=90°；
（2）利用勾股定理求出CE，再证△AEC∽△BAC，利用相似三角形对应边成比例求出半径；
【解析】（1）∵AB是⊙0的直径，∴∠AEB=90°，∴∠AEC=90°，∵CD=AD，∴DE=AD，∴∠DAE=∠DEA，
∵AO=OE，∴∠OAE=∠OEA，∴∠DEA+∠OEA=∠DAE+∠OAE=∠BAC=90°，∴OE⊥DE，∴DE与⊙0相切
（2）∵DE=2，∴AC=4，由勾股定理得：CE=，∵∠AEC=∠CAB=90°，∠C=∠C，
∴△AEC∽△BAC，∴AE：AB=CE：AC，即3：AB=：4，即AB=，∵OA=
六、(本大题共1小题，每小题12分，总计12分)
21、在庆祝中国共产党建党一百周年之际，合肥市瑶海区学校根据区教育局要求开展了“红心向党，爱我中华”演讲比赛。七年级、八年级根据初赛成绩各选出5名选手参加复赛。按照两个年级复赛成绩(满分100分)制成统计图如图所示。
（1）根据上图填写下表：
（2）结合两个年级选手复赛成绩的平均数和中位数，分析哪个年级的复赛成绩较好。
（3）如果从两个年级参加复赛成绩的前五名选手中选出2人代表学校参加区级比赛，求正好选出是同一个年级的选手的概率是多少？
【答案】
【分析】（1）利用求平均数的方法求出八年级平均数，再把七年级的成绩从小到大排列求出中位数
（2）在平均数相同情况下，中位数大的成绩好；
（3）列表展示所有20种等可能的结果数，再找出同一个年级的选手的结果数，然后根据概率公式求解。
【解析】（1）八年级的平均数为：（70+100+100+75+80）÷5=85； 七年级的中位数为：85；
（2）七、八年级的平均数相同，七年级的中位数高于八年级，七年级的复赛成绩较好。
（3）列表：
共有20种等可能的结果数，其中选出的两名同一个年级的选手的结果数为8，所以选出的同一个年级的选手的概率为：
七、(本大题共1小题，每小题12分，总计12分)
22、某汽车公司为确定一种型号的新能源汽车在高速公路上紧急刹车后滑行的距离y(单位m)与刹车时的速度大小x(单位：km/h)的函数关系。测得该汽车在速度大小为40km/h时，紧急刹车后滑行的距离为4m；速度大小为80km/h时，紧急刹车后滑行的距离为12m，已知紧急刹车后滑行的距离y(单位：m)与刹车时的速度大小x(单位：km/h)函数关系满足y=ax+bx
（1）求a、b的值；
（2）若两次测量中，刹车时的速度大小之差为20，滑行距离之差为6，求两次测量中，刹车时的速度大小的平均值。
【答案】
【分析】（1）待定系数法求出a、b的值；
（2）设两次速度大小分别为x1、x2；滑行距离分别为y1、y2；根据∣y1-y2∣=6，∣x1-x2∣=20求出（x1+x2）；
【解析】（1）将x=40、y=4；x=80、y=12代入y=ax+bx得：，解得：
（2）设两次速度大小分别为x1、x2；滑行距离分别为y1、y2；
∴∣y1-y2∣=∣（ax1+bx1）-（ax2+bx2）∣
=∣a（x1- x1）+b（x1- x2）∣
=∣a（x1+x2）（x1- x2）+b（x1- x2）∣
即：∣（x1+x2）×20+×20∣=6，∴（x1+x2）+1=±6，解得x1+x2=200或x1+x2=-280（舍去）
∴（x1+x2）=100（km/h）
八、(本大题共1小题，每小题14分，总计14分)
23、如图1，在△ABC中，AB=AC=5、BC=8、点P、Q分别在射线CB、AC上(点P不与C，B重合)，且保持∠APQ=∠ABC。
（1）若P在线段CB上，求证：△ABP△PCQ；
（2）设BP=x、CQ=y，求y与x之间的函数关系式，并写出x的取值范围；
（3）如图2，正方形ABCD的边长为5，点P、Q分别在直线CB、DC上(点P不与C、B重合)，且保持∠APQ=90°，当CQ=1时，直接写出BP的长。
【答案】
【分析】（1）求线段CQ的长，根据已知条件AB=AC，∠APQ=∠ABC知道，可以先证明△QCP∽△PBA，由比例关系式得出；
（2）要求y与x之间的函数关系式，函数的定义域，因为BP在线段CB上，或在CB的延长线上，根据实际情况证明△QCP∽△ABP，求出比例关系式得出；
（3）要求线段BP的长，先证明△BAP∽△CPQ得出比例式，再利用图形间的“和差“关系求解．
【解析】（1）∵∠APQ+∠CPQ=∠B+∠BAP，∠APQ=∠ABC，∴∠BAP=∠CPQ．又∵AB=AC，∴∠B=∠C．
∴△CPQ∽△BAP．∴CQ：BP＝CP：AB．∵AB=AC=5，BC=8，BP=6，CP=8-6=2，∴CQ：6＝2：5，CQ＝．
（2）（ = 1 \* rman i）若点P在线段CB上，由（1）知CQ：BP＝CP：AB，∵BP=x，BC=8，∴CP=BC-BP=8-x，又∵CQ=y，AB=5，
∴y：x＝（8−x）：5，即y＝−x+x．故所求的函数关系式为y＝−x+x（0＜x＜8）．
（ = 2 \* rman ii）若点P在线段CB的延长线上，如图．∵∠APQ=∠APB+∠CPQ，∠ABC=∠APB+∠PAB，∠APQ=∠ABC，∴∠CPQ=∠PAB．又∵∠ABP=180°-∠ABC，∠PCQ=180°-∠ACB，∠ABC=∠ACB，∴∠ABP=∠PCQ．∴△QCP∽△PBA．
∴BP：CQ＝AB：PC．∵BP=x，CP=BC+BP=8+x，AB=5，CQ=y，∴x：y＝5：（8+x），即y＝−x+x（x＞0）．
（3）①当点P在线段BC上，∵∠APQ=90°，∴∠APB+∠QPC=90°，∵∠PAB+∠APB=90°，∴∠PAB=∠QPC，∵∠B=∠C=90°，∴△ABP∽△PCQ，∴AB：PC=BP：CQ，即5：（5-BP）=BP：1，解得：BP＝，或BP＝，
②当点P在线段BC的延长线上，则点Q在线段DC的延长线上，同理可得：△ABP∽△PCQ，∴AB：PC=BP：CQ，
∴5：（BP-5）=BP：1，解得：BP＝，
③当点P在线段CB的延长线上，则点Q在线段DC的延长线上，同理可得：△ABP∽△PCQ，∴AB：PC=BP：CQ，
∴5：（BP+5）=BP：1，解得：BP＝．
综上所述，BP＝或BP＝或BP＝或BP＝．
平均数(分)
中位数(分)
众数(分)
七年级
85
85
八年级
80
100
七1
七2
七3
八1
八2
七1
（七2，七1）
（七3，七1）
（八1，七1）
（八2，七1）
七2
（七1，七2）
（七3，七2）
（八1，七2）
（八2，七2）
七3
（七1，七3）
（七2，七3）
（八1，七3）
（八2，七3）
八1
（七1，八1）
（七2，八1）
（七3，八1）
（八2，八1）
八2
（七1，八2）
（七2，八2）
（七3，八2）
（八1，八2）