

2022年山东省滨州市滨城区中考一模数学试题
展开二O二二年九年级复习质量检测
数学试题(A)
温馨提示:
1.本试卷分第Ⅰ卷和第Ⅱ卷两部分,共8页。满分120分。考试用时120分钟。
2.答卷前,考生务必用0.5毫米黑色签字笔将自己的学校、姓名、准考证号填写在答题卡中规定的位置上。
3.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。答案不能答在试题卷上。
4.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带。不按以上要求作答的答案无效。
第Ⅰ卷(选择题共36分)
一、选择题:本大题共12个小题,在每小题的四个选项中只有一个是正确的,请把正确的选项选出来,用2B铅笔把答题卡上对应题目的答案标号涂黑.每小题涂对得3分,满分36分。
1.下列图形,线段、等边三角形、平行四边形、圆,其中既是轴对称图形,又是中心对称图形的个数为( )
A.1 B.2 C.3 D.4
2.下列运算正确的是( )
A.3m+2n=6mn B.
C.(2a-b)2=4a2-b2 D.
3.如图,直线AB∥EF,点C是直线AB上一点,点D是直线AB外一点,若∠BCD=95°,∠CDE=25∘,则∠DEF的度数是( )
A.110° B.115° C.120° D.125°
4.若,则x,y的值为( )
A. B. C. D.
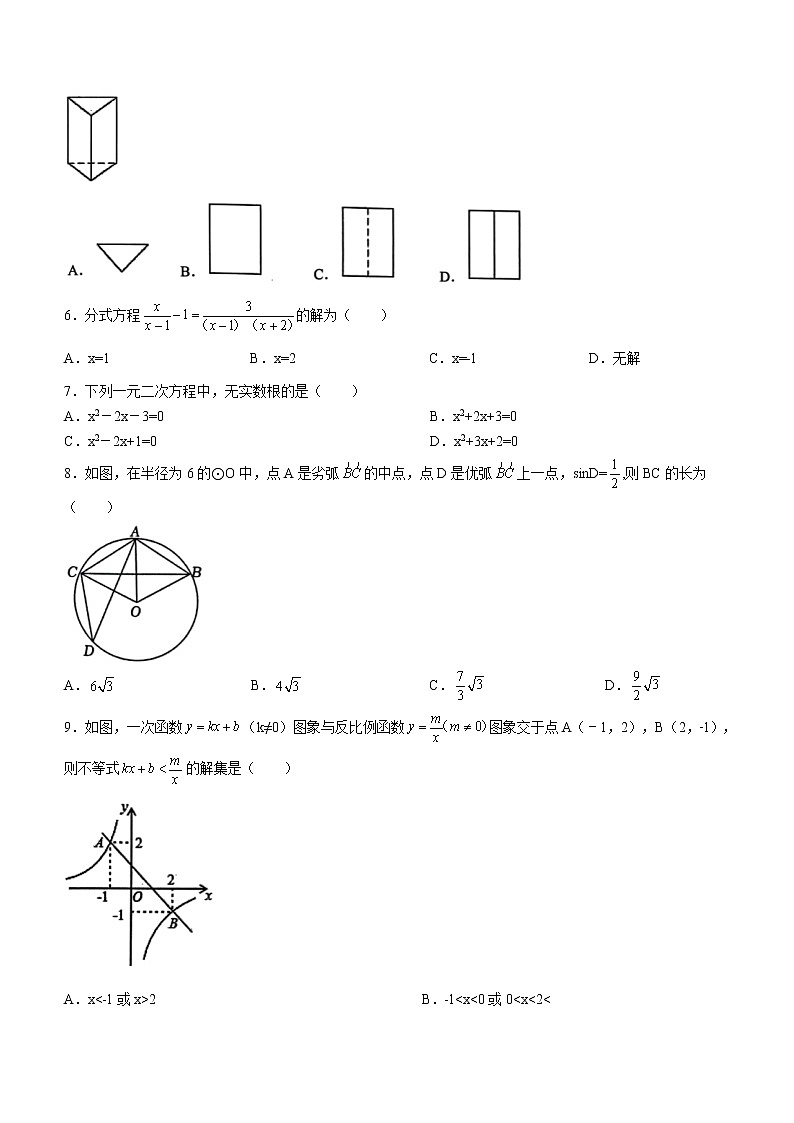
5.如图,该几何体的主视图是( )
6.分式方程的解为( )
A.x=1 B.x=2 C.x=﹣1 D.无解
7.下列一元二次方程中,无实数根的是( )
A.x2-2x-3=0 B.x2+2x+3=0
C.x2-2x+1=0 D.x2+3x+2=0
8.如图,在半径为6的⊙O中,点A是劣弧的中点,点D是优弧上一点,sinD=,则BC的长为( )
A. B. C. D.
9.如图,一次函数(k≠0)图象与反比例函数图象交于点A(﹣1,2),B(2,﹣1),则不等式的解集是( )
A.x<﹣1或x>2 B.﹣1<x<0或0<x<2<
C.x<﹣1或0<x<2 D.﹣1<x<0或x>2
10.如图,∠MON=40°,以O为圆心,4为半径作弧交OM于点A,交ON于点B,分别以点A,B为圆心,大于的长为半径画弧,两弧在∠MON的内部相交于点C,画射线OC交于点D,E为OA上一动点,连接BE,DE,则阴影部分周长的最小值为( )
A. B. C. D.
11.已知二次函数的图象如图所示,则下列结论正确的是( )
A.abc<0 B.a-b+c<0 C.4a-2b+c>0 D.b>2a
12.如图,在Rt△ABC中,AB=AC=10,∠BAC=90°,等腰直角三角形ADE绕点A旋转,∠DAE=90°,AD=AE=4,连接DC,点M、P、N分别为DE、DC、BC的中点,连接MP、PN、MN。
①△PMN为等腰直角三角形;②;③△PMV面积的最大值是;④△PMN周长的最小值为。正确的结论有( )
A.4个 B.3个 C.2个 D.1个
第Ⅱ卷(非选择题共84分)
二、填空题(共6小题,满分24分,每小题4分)
13.若在实数范围内有意义,则实数x的取值范围是_________。
14.如图,在Rt△ABC中,∠C=90∘,AF=EF.若∠CFE=70°,则∠B=___________°。
15.在平面直角坐标系中,点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB放大到原来的2倍,则点P的对应点的坐标为__________。
16.如图,⊙O是正五边形ABCDE的外接圆,点P为ED上的一点,则∠APC的度数为____________。
17.如图,在平面直角坐标系中,菱形ABCD的边BC与x轴平行,A,B两点纵坐标分别为4,2,反比例函数经过A,B两点,若菱形ABCD面积为8,则k值为____________。
18.如图,在矩形ABCD中,AB=4,,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若,则CE=_________。
三、解答题:(本大题共6个小题,满分60分。解答时请写出必要的推演过程。)
19.(12分)(1)计算:
(2)先化简:,然后从中的解集选一个。
20.(8分)为落实关于开展中小学课后服务工作的要求,某学校开展了四门校本课程供学生选择:A.趣味数学;B.博乐阅读;C.快乐英语;D.硬笔书法。全校共有100名学生选择了A课程,为了解选A课程学生的学习情况,从这100名学生中随机抽取了30名学生进行测试.将他们的成绩(百分制)绘制成频数分布
直方图。
(1)其中70≤x<80这一组的数据为74,73,72,75,76,76,79,则这组数据的中位数是_______,众数是_________。
(2)根据题中信息,估计该校共有________人,选A课程学生成绩在80≤x<90的有________人。
(3)如果学校规定每名学生要选两门不同的课程,小张和小王在选课中,若第一次都选了课程C,那么他俩第二次同时选课程A或B的概率是多少?请用列表法或画树状图的方法加以说明。
21.(8分)如图,在口ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF。
(1)求证:四边形ABEF是菱形;
(2)若AE=2,,CE=1,求 ABCD的面积。
22.(12分)某水果连锁店销售热带水果,其进价为20元/千克,销售一段时间后发现:该水果的日销售y(千克)与售价x(元/千克)的函数图象关系如图所示:
(1)求y关于x的函数解析式;
(2)当售价为多少元/千克时,当日销售利润最大,最大利润为多少元?
(3)由于某种原因,该水果进价提高了m元/千克(m>0),物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系。若日销售最大利润是1280元,请写出m的值。
23.(8分)如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆。
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长。
24.(12分)在平面直角坐标系中,过点A(3,4)的抛物线与x轴交于点B(﹣1,0),与y轴交于点C,过点A作AD⊥x轴于点D。
(1)求抛物线的解析式.
(2)如图1,点P是直线AB上方抛物线上的一个动点,连接PD交AB于点Q,连接AP,当S△AQP=4S△APQ时,求点P的坐标。
(3)如图2,点G是线段OC上一个动点,连结DG,求最小值。
二〇二二年九年级复习质量检测
数学试题参考答案(A)
一、选择题
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
B | D | C | D | D | D | B | C | D | A | D | C |
二、填空题
l3.x>﹣1且x≠0 14.55 15.(2m,2n)或(﹣2m,﹣2n)
16.﹣72° 17. 18.
三、解答题
19.解:(1)原式=;………………4分
(2)因为
∵解不等式①得:x>﹣2,
解不等式②得:x<3,
∴不等式组的解集为﹣2<x<3.………………8分
原式=
=
=…………………………………………10分
∵x≠﹣2,0,1,4
当x=﹣l时,原式=1,或
当x=2时,原式=……………………………12分(两个答案都可以)
20.解:(1)把这些数从小到大排列为72,73,74,75,76,76,79,
则这组数据的中位数是75,众数是76;
答案为:75,76;(每空1分)
(2)估计该校共有学生人数有:100÷20%=500(人),
答案为:500,150;(每空1分)
(3)根据题意列树状图如下:
……………………7分
共有9种等可能的结果数,其中他俩第二次同时选择课程A或课程B的有2种,
则他俩第二次同时选择课程A或课程B的概率是 …………………8分
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠DAE=∠AEB,
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE,同理可得AB=AF,
∴AF=BE,
∴四边形ABEF是平行四边形,………………………3分
∵AB=AF.
∴四边形ABEF是菱形.…………………………4分
(2)解:作FG⊥BC于G,
∵四边形ABEF是菱形,若AE=2,BF=,
∴AE⊥BF,,
∴,
∵,
∴,
∴ ………………………8分
22.解:(1)设(k,b为常数,k≠0)
根据题意得:,解得:,
∴y关于x的函数解析式为y=﹣2x+160;……………………………4分
(2)设当该商品的售价是x元/件时,日销售利润为w元,
根据题意得:w=(﹣2x+160)(x-20)=﹣2x2+200x-3200=﹣2(x-50)2+1800
∴当x=50时w有最大值,最大值为1800(元),……………………………8分
答:当该商品的售价是50元/件时,日销售利润最大,最大利润是1800元;
(3)根据题意得,w=(x-20-m)(﹣2x+160)=﹣2x2+(200+2m)x-3200-160m,
∵对称轴为直线,
∴①当时(舍),②当时(舍),③当x=40时,w取最大值为1280,
解得:m=4 ………………………………12分
23.解:(1)如图,连接OE,
∵ED⊥EB,
∴∠DEB=90°,
∴BD是⊙O的直径,
∵OB=OE,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠OBE=∠CBE,
∴∠OEB=∠CBE,
∴OE//BC,
又∵∠C=90°,
∴∠AEO=90°,即OE⊥AC,
∴AC为⊙O的切线;……………………………4分
(2)∵ED⊥BE,
∴∠BED=∠C=90°,
又∵∠DBE=∠EBC,
∴△BDE∽△BEC,
∴,
∴,
∵∠AEO=∠C=90°,∠A=∠A,
∴△AOE∽△ABC,
∴,解得:………………………8分
24.解:(1)将点A(3,4),B(﹣1,0)代入,
得:,
解得,
∴;………………………………………………3分
(2)如图1,过点P作PE//x轴,交AB于点E,
∵A(3,4),AD⊥x轴,
∴D(3,0),
∵B(﹣1,0),
∴BD=3-(﹣1)=4,
∵S△AQD=4S△APQ,△AQD与△APQ是等高的两个三角形,
∴
∵PE//x轴,
∴△PQE∽△DQB,
∴,
∴
∴PE=1,
∴可求得直线AB的解析式为y=x+1,
设E(x,x+1),则P(x-1,x+1),
将点P坐标代入y=﹣x2+3x+4得﹣(x-1)2+3(x-1)+4=x+1,
解得,
当时,,
∴点P;
当时, ,
∴点P,
∵点P是直线AB上方抛物线上的一个动点,
∴﹣1<x-1<3,
∴点P的坐标为点P或P …………………8分
(3)如图,
连接CB,过点D作DM⊥BC交BC于点M
∵BO=1,CO=4
∴
∴
的最小值为………………………12分
2023年山东省滨州市滨城区中考二模数学试题(含解析): 这是一份2023年山东省滨州市滨城区中考二模数学试题(含解析),共23页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2023年山东省滨州市滨城区中考数学模拟试卷(含答案): 这是一份2023年山东省滨州市滨城区中考数学模拟试卷(含答案),共25页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2023年山东省滨州市滨城区中考数学模拟试卷(含解析): 这是一份2023年山东省滨州市滨城区中考数学模拟试卷(含解析),共24页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。












