初中数学湘教版九年级下册2.5 直线与圆的位置关系复习课件ppt

这是一份初中数学湘教版九年级下册2.5 直线与圆的位置关系复习课件ppt，共24页。PPT课件主要包含了2016·南宁，2016·北海，切线的判定，圆周角定理，垂径定理，∵OA是⊙O的半径，BC⊥OA，∴BC为⊙O的切线，AB⊥BC，或∠ABC90˚等内容，欢迎下载使用。

2019年中考说明中有关圆的内容
1.掌握垂径定理： 垂直于弦的直径平分弦以及弦所对的两条弧。2.掌握切线的概念， 探索切线与过切点的半径的关系. 会用三角尺过圆上一点画圆的切线。3.会计算圆的弧长、扇形的面积.
（知识要点：圆周角、圆心角、弧长 能力：理解）
知识要点：垂径定理、圆周角定理、 切线 、三角函数 能力：理解、运用
知识要点：圆周角定理、四边形的内角和 能力：了解、运用
知识要点：圆、 切线 、垂径定理、勾股定理 能力：理解、运用
知识要点：菱形、扇形的面积 能力：了解、运用
近几年有关圆的热点考点
4.弧长、扇形面积公式
经过半径的外端并且垂直于这条半径的直线是圆的切线.
如图，△ABC的一边AB是⊙O的直径，请你添加一个条件，使BC是⊙O的切线，你所添加的条件为 .
（中考突破第121页第9题）
已知：如图，在△ABC中，BC=AC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC,垂足为点E.判断DE与⊙O的位置关系，并证明你的结论.
（中考突破第122页第24题）
解：DE是⊙O的切线.理由是： 如图， 连接OD， 则OD是⊙O的半径 ∵OB=OD,BC=AC∴∠A=∠B,∠1=∠B∴∠A=∠1 ∴OD∥AC∵DE⊥AC ∴ DE⊥OD∴DE是⊙O的切线.
如图，已知AO为Rt△ABC的角平分线，∠ACB=90°， ,以O为圆心，OC为半径的圆分别交AO，BC于点D，E,连接ED并延长交AC于点F. 求证：AB是⊙O的切线.
（中考突破第190页第2题）
解： 如图，过点O作OG⊥AB于点G ∵∠ACB=90˚ ∴OC⊥AC ∵ AO为∠BAC的平分线 ∴OC=OG ∵OC是⊙O的半径 ∴OG是⊙O的半径 ∴AB是⊙O的切线.
证明切线时，添加辅助线的方法
先说方法，后口述解题过程
如图，PA是⊙O的切线，A是切点，AC是直径，AB是弦，连接PB、PC,PC交AB于点E，且PA=PB. 求证：PB是⊙O的切线.
如图，在Rt△ABC中，∠C=90°，BD是角平分线，点O在AB上，以点O为圆心，OB为半径的圆经过点D，交BC于点E． 求证：AC是⊙O的切线.
如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连结AC，过 上一点E作EG∥AC交CD的延长线于点G，连结AE交CD于点F，且EG=FG，连结CE． 求证：EG是⊙O的切线.
（2017南宁、北海、钦州、防城港）
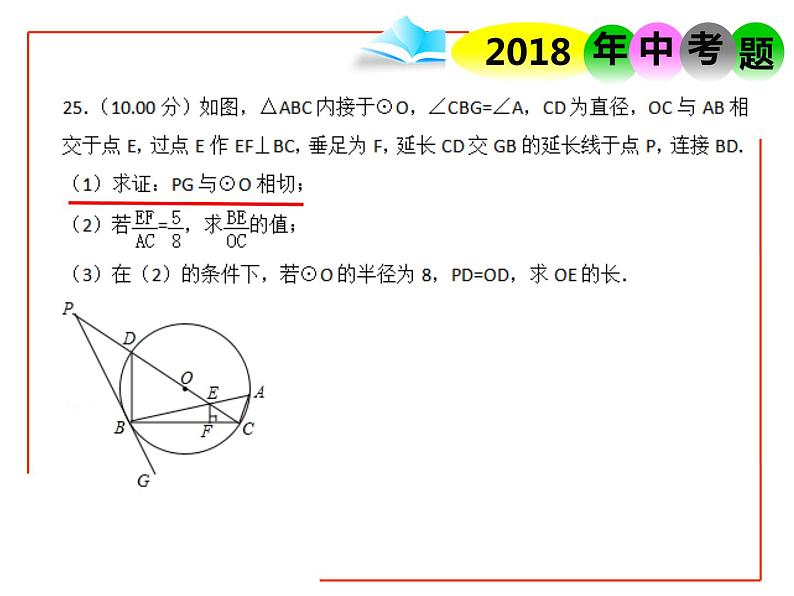
如图，△ABC内接于⊙O，∠CBG=∠A，CD为直径，OC与AB相交于点E，过点E作EF⊥BC，垂足为F，延长CD交GB的延长线于点P，连接BD． 求证：PG与⊙O相切.
通过本节课的学习，我的收获是…… 我的疑惑是……
必做题：中考突破121页 第13题 选做题：中考突破122页 第23题 或 中考突破190页 第2题
如图，已知在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过D作DE⊥AC于点E，CD＝ ，∠ACB＝30°.求证：DE是⊙O的切线 .
证明：如图，连接OD则OD是⊙O的半径 ∵AB=AC,OB=OD∴∠B＝∠C,∠B＝∠1∴∠C＝∠1 ∴OD∥AC∵DE⊥AC∴AD⊥OD∴DE是⊙O的切线.