

2022年中考压轴微专题:反比例函数实际问题(无答案)
展开2022中考压轴微专题:反比例函数实际问题
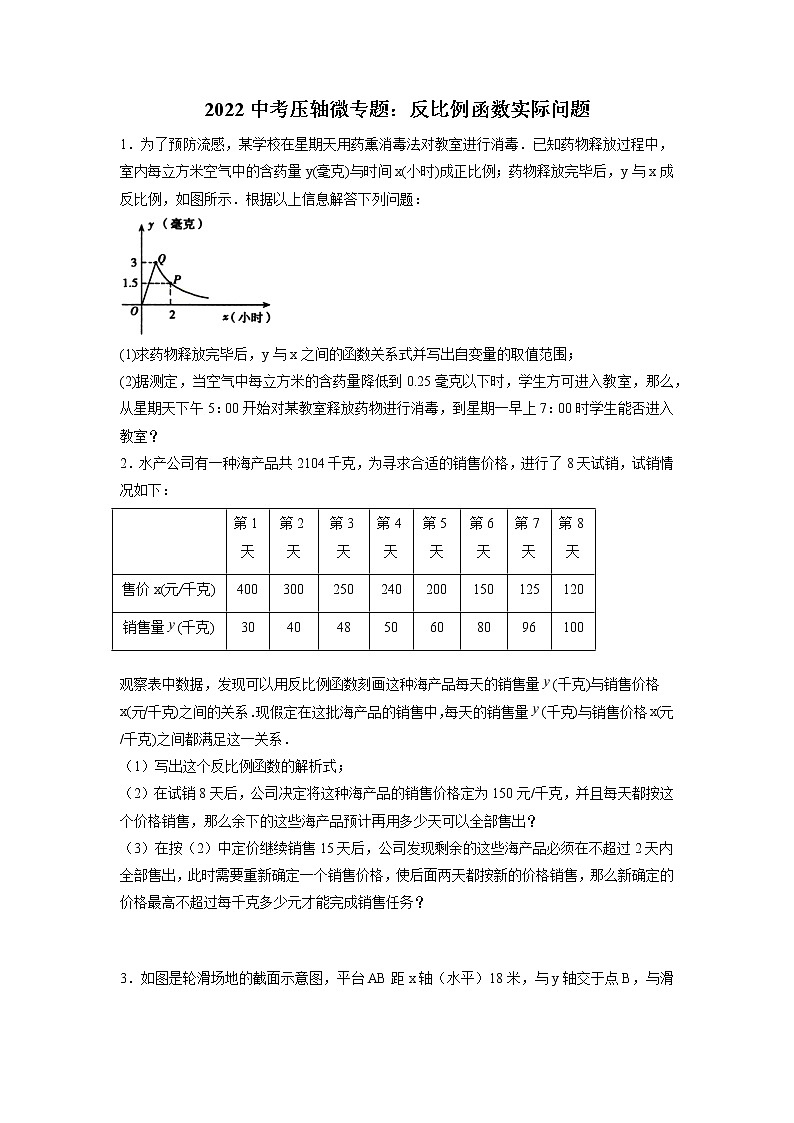
1.为了预防流感,某学校在星期天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(小时)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据以上信息解答下列问题:
(1)求药物释放完毕后,y与x之间的函数关系式并写出自变量的取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进入教室,那么,从星期天下午5:00开始对某教室释放药物进行消毒,到星期一早上7:00时学生能否进入教室?
2.水产公司有一种海产品共2104千克,为寻求合适的销售价格,进行了8天试销,试销情况如下:
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | 第8天 |
售价x(元/千克) | 400 | 300 | 250 | 240 | 200 | 150 | 125 | 120 |
销售量(千克) | 30 | 40 | 48 | 50 | 60 | 80 | 96 | 100 |
观察表中数据,发现可以用反比例函数刻画这种海产品每天的销售量(千克)与销售价格x(元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量(千克)与销售价格x(元/千克)之间都满足这一关系.
(1)写出这个反比例函数的解析式;
(2)在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?
(3)在按(2)中定价继续销售15天后,公司发现剩余的这些海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?
3.如图是轮滑场地的截面示意图,平台AB距x轴(水平)18米,与y轴交于点B,与滑道y=(x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.
(1)求k,并用t表示h;
(2)设v=5.用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及y=13时运动员与正下方滑道的竖直距离;
(3)若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.
4.某一农家计划利用已有的一堵长为8m的墙,用篱笆圈成一个面积为12m2的矩形ABCD花园,现在可用的篱笆总长为11m.
(1)若设,.请写出y关于x的函数表达式;
(2)若要使11m的篱笆全部用完,能否围成面积为15m2的花园?若能,请求出长和宽;若不能,请说明理由;
(3)若要使11m的篱笆全部用完,请写出y关于x的第二种函数解析式.请在坐标系中画出两个函数的图象,观察图象,满足条件的围法有几种?请说明理由.
5.某超市一段时期内对某种商品经销情况进行统计分析:得到该商品的销售数量(件)由基础销售量与浮动销售量两个部分组成,其中基本销售量保持不变,浮动销售量与售价x(元/件,)成反比例,销售过程中得到的部分数据如下:
售价x | 8 | 10 |
销售数量 | 70 | 58 |
(1)求与x之间的函数关系式;
(2)当该商品销售数量为50件时,求每件商品的售价;
(3)设销售总额为,求的最大值.
6.六•一儿童节,小文到公园游玩.看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等,比如:A、B、C是弯道MN上的三点,矩形ADOG、矩形BEOH、矩形CFOI的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S1、S2、S3,并测得S2=6(单位:平方米).OG=GH=HI.
(1)求S1和S3的值;
(2)设T(x,y)是弯道MN上的任一点,写出y关于x的函数关系式;
(3)公园准备对区域MPOQN内部进行绿化改造,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?
7.如图是某电脑公司的销售额y(万元)关于时间x(月)之间的函数图象,其中前几个月两变量之间满足反比例函数关系,后几个月两变量之间满足一次函数关系,观察图象,回答下列问题:
该年度________月份的销售额最低;
求出该年度最低的销售额;
若电脑公司月销售额不大于万元,则称销售处于淡季.在这年中,该电脑公司哪几个月销售处于淡季?
8.超越公司将某品牌农副产品运往新时代市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从超越公司出发,能否在上午10:00之前到达新时代市场?请说明理由.
9.媒体报道,近期“手足口病”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所
示(即图中线段OA和双曲线在A点及其右侧的部分),根据图象所示信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的函数关系式及自变量的取值范围;
(2)据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在多长时间内,师生不能进入教室?
10.某气球内充满了一定质量的气体,当温度不变时,气球内的气压p(kpa)是气体体积v(m3)的反比例函数,其图象如图所示.
(1)写出这一函数的表达式;
(2)当气球体积1.5m3为时,气压是多少?
(3)当气球内的气压大于144kpa时,气球将爆炸,为了安全起见,气球的体积应不小于多少?
11.小强的妈妈想在自家的院子里用竹篱笆围一个面积为4平方米的矩形小花园,妈妈问九年级的小强至少需要几米长的竹篱笆(不考虑接缝).
小强根据他学习函数的经验做了如下的探究.下面是小强的探究过程,请补充完整:
建立函数模型:
设矩形小花园的一边长为x米,篱笆长为y米.则y关于x的函数表达式为________;列表(相关数据保留一位小数):
根据函数的表达式,得到了x与y的几组值,如下表:
x | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
y | 17 | 10 | 8.3 |
| 8.2 | 8.7 | 9.3 |
| 10.8 | 11.6 |
描点、画函数图象:
如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点画出该函数的图象;
观察分析、得出结论:
根据以上信息可得,当x=________时,y有最小值.
由此,小强确定篱笆长至少为________米.
12.某医药研究所研制并生产治疗同一种病的两种新药,经过统计,有两个成年人同时按正常药量服用,1小时后,服用药品的血液中含药量(微克/毫升)与时间x(小时)满足反比例函数,服用药品的血液中含药量(微克/毫升与时间x(小时)满足二次函数,如图所示,且在3小时,含药量达到最大值为8微克/毫升,
(1)求k以及的值;
(2)当服用药品的血液中含药量为3.5微克/毫升时,求的值;
(3)若血液中药品含量不低于6.5微克/毫升时,药品含量在0.75微克/毫升与4.5微克/毫升之间(包括0.75和4.5)时为疗效时间,求这两种药品均起疗效的时间有多长?(结果保留根号)
13.我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为 的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度 随时间 (小时)变化的函数图象,其中 段是双曲线 的一部分.请根据图中信息解答下列问题:
(1) 恒温系统在这天保持大棚内温度 的时间有多少小时?
(2) 求 的值;
(3) 当棚内温度不低于 时,该蔬菜能够快速生长,请问这天该蔬菜能够快速生长多长时间?
14.心理学家研究发现,一般情况下,在一节 分钟的课中,学生的注意力随教师讲课时间的变化而变化,开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散,经过实验分析可知,学生的注意力 随时间 (分)的变化规律如图所示,其中 , 分别为线段, 为双曲线的一部分.
(1) 写出线段 和双曲线 的函数关系式(不要求指出自变量取值范围):
线段 : .
双曲线 : .
(2) 开始上课后第 分钟时的注意力水平为 ,第 分钟时的注意力水平为 ,则 , 的大小关系是 .
(3) 在一节课中,学生大约最长可以连续保持 分钟(精确到 分钟),使得注意力维持在 以上.
15.某气象研究中心观测到一场沙尘暴从发生到减弱的全过程,风速 (千米/小时)与时间 (小时)的函数图象如图所示.开始一段时间,风速平均每小时增加 千米, 小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加 千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速 (千米/小时)与时间 (小时)成反比例函数关系缓慢减弱.
(1) 这场沙尘暴的最高风速是 千米/小时,最高风速维持了 小时;
(2) 当 时,求出风速 (千米/小时)与时间 (小时)之间的函数关系式;
(3) 在这次沙尘暴形成的过程中,当风速不超过 千米/小时时称为“安全时刻”,其余时刻称为“危险时刻”,那么在沙尘暴整个过程中,“危险时刻”共有 小时.
2024年中考数学反比例函数专题---选择题专题(压轴)(解析): 这是一份2024年中考数学反比例函数专题---选择题专题(压轴)(解析),共19页。试卷主要包含了【答案】C,【答案】A,【答案】D,【答案】B等内容,欢迎下载使用。
2022年中考数学专题复习反比例函数压轴题: 这是一份2022年中考数学专题复习反比例函数压轴题,共101页。试卷主要包含了的图象经过点F,交AB于点G,的图象经过点B,材料等内容,欢迎下载使用。
2022中考复习微专题实际问题与反比例函数: 这是一份2022中考复习微专题实际问题与反比例函数,共8页。












