2022年九年级数学中考专题训练+圆的有关概念与性质（有答案）

这是一份2022年九年级数学中考专题训练+圆的有关概念与性质（有答案），共7页。
1．(2021·枣庄模拟)如图，△ABC的顶点均在⊙O上，若∠A＝36°，则∠BOC的度数为( )
A．18°B．36°C．60°D．72°
2．(2021·四川凉山州)点P是⊙O内一点，过点P的最长弦的长为10 cm，最短弦的长为6 cm，则OP的长为( )
A．3 cmB．4 cmC．5 cmD．6 cm
3．(2021·四川广安)如图，公园内有一个半径为18米的圆形草坪，从A地走到B地有观赏路(劣弧AB)和便民路(线段AB)．已知A，B是圆上的点，点O为圆心，∠AOB＝120°，小强从A走到B，走便民路比走观赏路少走________米．( )
A．6π－6eq \r(3)B．6π－9eq \r(3)
C．12π－9eq \r(3)D．12π－18eq \r(3)
4．(2021·枣庄模拟)如图，BD为⊙O的直径，点A为eq \(BDC,\s\up8(︵))的中点，∠ABD＝35°，则∠DBC＝( )
A．20°B．35°C．15°D．45°
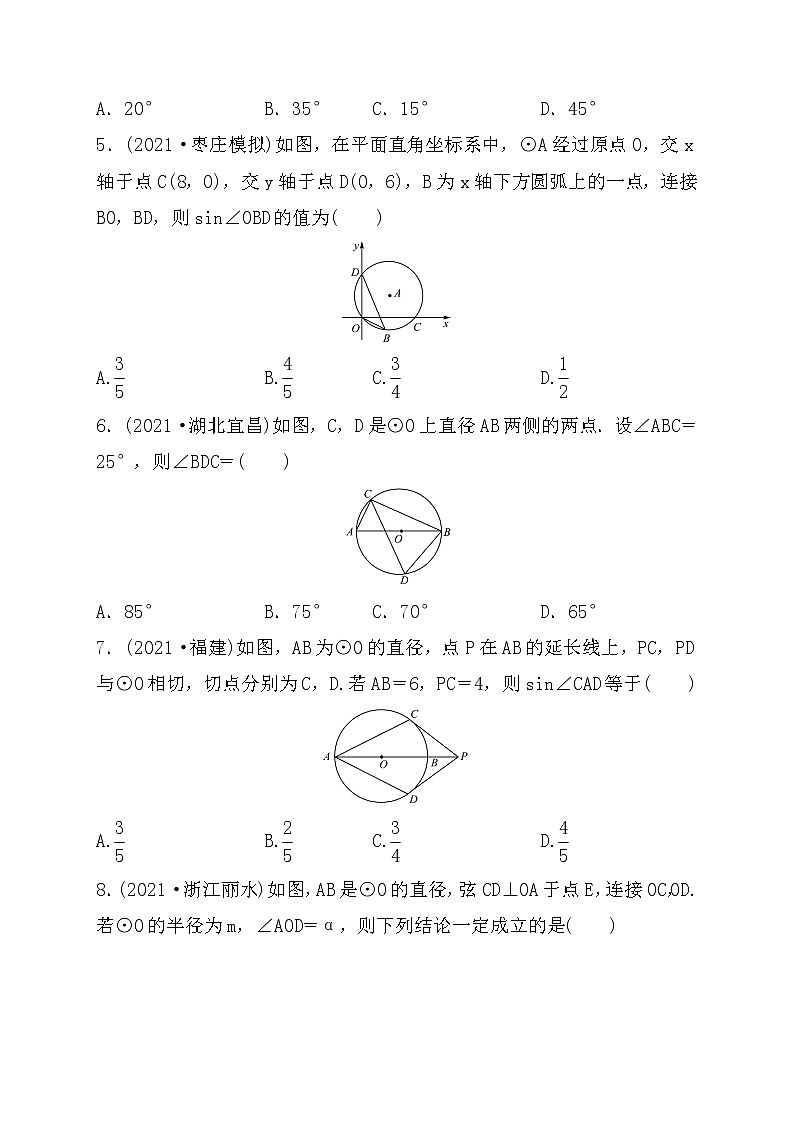
5．(2021·枣庄模拟)如图，在平面直角坐标系中，⊙A经过原点O，交x轴于点C(8，0)，交y轴于点D(0，6)，B为x轴下方圆弧上的一点，连接BO，BD，则sin∠OBD的值为( )
A.eq \f(3,5)B.eq \f(4,5)C.eq \f(3,4)D.eq \f(1,2)
6．(2021·湖北宜昌)如图，C，D是⊙O上直径AB两侧的两点．设∠ABC＝25°，则∠BDC＝( )
A．85°B．75°C．70°D．65°
7．(2021·福建)如图，AB为⊙O的直径，点P在AB的延长线上，PC，PD与⊙O相切，切点分别为C，D.若AB＝6，PC＝4，则sin∠CAD等于( )
A.eq \f(3,5)B.eq \f(2,5)C.eq \f(3,4)D.eq \f(4,5)
8．(2021·浙江丽水)如图，AB是⊙O的直径，弦CD⊥OA于点E，连接OC，OD.若⊙O的半径为m，∠AOD＝α，则下列结论一定成立的是( )
A．OE＝m·tan α B．CD＝2m·sin α
C．AE＝m·cs α D．S△COD＝eq \f(1,2)m2·sin α
9．(2021·湖北鄂州)筒车是我国古代发明的一种水利灌溉工具，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理，如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆，如图2.已知圆心O在水面上方，且⊙O被水面截得的弦AB长为6米，⊙O半径长为4米．若点C为运行轨道的最低点，则点C到弦AB所在直线的距离是( )

图1 图2
A．1米 B．(4－eq \r(7))米
C．2米 D．(4＋eq \r(7))米
10．(2021·江苏连云港)如图，OA，OB是⊙O的半径，点C在⊙O上，∠AOB＝30°，∠OBC＝40°，则∠OAC＝________°.
11．(2021·四川成都)如图，在平面直角坐标系xOy中，直线y＝eq \f(\r(3),3)x＋eq \f(2\r(3),3)与⊙O相交于A，B两点，且点A在x轴上，则弦AB的长为________．
12．(2021·烟台)如图，在正方形网格中，每个小正方形的边长都是1，⊙O是△ABC的外接圆，点A，B，O在网格线的交点上，则sin∠ACB的值是________．
13．(2021·安徽)如图，⊙O中两条互相垂直的弦AB，CD交于点E.
(1)点M是CD的中点，OM＝3，CD＝12，求⊙O的半径长；
(2)点F在CD上，且CE＝EF，求证：AF⊥BD.
14．(2021·北京)如图，⊙O是△ABC的外接圆，AD是⊙O的直径，AD⊥BC于点E.
(1)求证：∠BAD＝∠CAD；
(2)连接BO并延长，交AC于点F，交⊙O于点G，连接GC.若⊙O的半径为5，OE＝3，求GC和OF的长．
15．(2021·江苏苏州)如图，四边形ABCD内接于⊙O，∠1＝∠2，延长BC到点E，使得CE＝AB，连接ED.
(1)求证：BD＝ED；
(2)若AB＝4，BC＝6，∠ABC＝60°，求tan∠DCB的值．
参考答案
1．D 2.B 3.D 4.A 5.A 6.D 7.D 8.B 9．B
10．25 11.2eq \r(3) 12.eq \f(2\r(5),5)
13．(1)解：⊙O的半径长为3eq \r(5).
(2)证明：连接AC，延长AF交BD于点G，如图．
∵AB⊥CD，CE＝EF，
∴AB是CF的垂直平分线，
∴AF＝AC，即△ACF是等腰三角形．
∵CE＝EF，∴∠FAE＝∠CAE.
∵eq \(BC,\s\up8(︵))＝eq \(BC,\s\up8(︵))，∴∠CAE＝∠CDB，
∴∠FAE＝∠CDB.
∵在Rt△BDE中，∠CDB＋∠B＝90°，∴∠FAE＋∠B＝90°，
∴∠AGB＝90°，∴AG⊥BD，即AF⊥BD.
14．(1)证明：∵AD是⊙O的直径，AD⊥BC，
∴eq \(BD,\s\up8(︵))＝eq \(CD,\s\up8(︵))，∴∠BAD＝∠CAD.
(2)解：GC＝6；OF＝eq \f(25,11).
15.(1)证明：∵四边形ABCD内接于⊙O，∴∠A＋∠BCD＝180°.
∵∠DCE＋∠BCD＝180°，∴∠A＝∠DCE.
∵∠1＝∠2，∴eq \(AD,\s\up8(︵))＝eq \(DC,\s\up8(︵))，∴AD＝DC.
在△ABD和△CED中，eq \b\lc\{(\a\vs4\al\c1(AB＝CE，,∠A＝∠DCE，,AD＝DC，))
∴△ABD≌△CED(SAS)，∴BD＝ED.
(2)解：tan∠DCB＝eq \f(5\r(3),3).