2022北京中考数学一轮复习系列系列——三角形（学生版）

这是一份2022北京中考数学一轮复习系列系列——三角形（学生版），共25页。试卷主要包含了已知锐角∠AOB，如图，，如图所示，点P到直线l的距离是等内容，欢迎下载使用。
2022年北京中考数学一轮复习系列系列——（05）三角形
五年中考
一．选择题（共3小题）
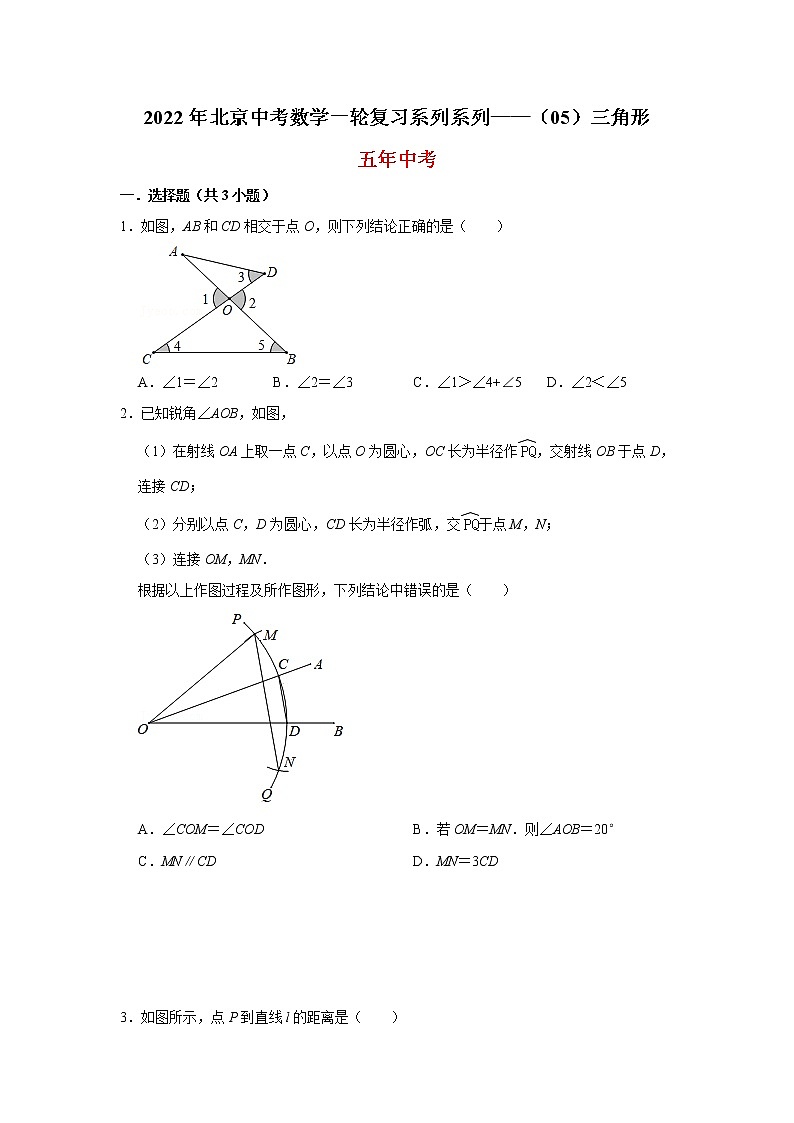
1．如图，AB和CD相交于点O，则下列结论正确的是（　　）

A．∠1＝∠2 B．∠2＝∠3 C．∠1＞∠4+∠5 D．∠2＜∠5
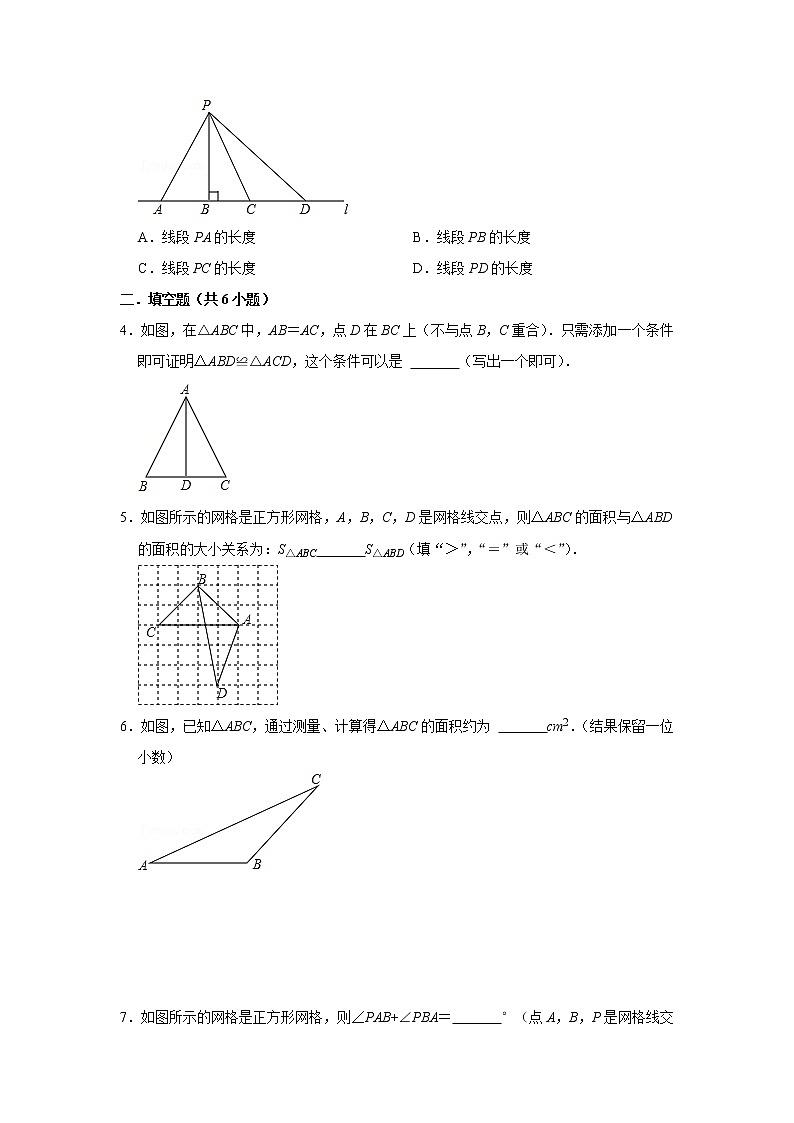
2．已知锐角∠AOB，如图，
（1）在射线OA上取一点C，以点O为圆心，OC长为半径作，交射线OB于点D，连接CD；
（2）分别以点C，D为圆心，CD长为半径作弧，交于点M，N；
（3）连接OM，MN．
根据以上作图过程及所作图形，下列结论中错误的是（　　）

A．∠COM＝∠COD B．若OM＝MN．则∠AOB＝20°
C．MN∥CD D．MN＝3CD




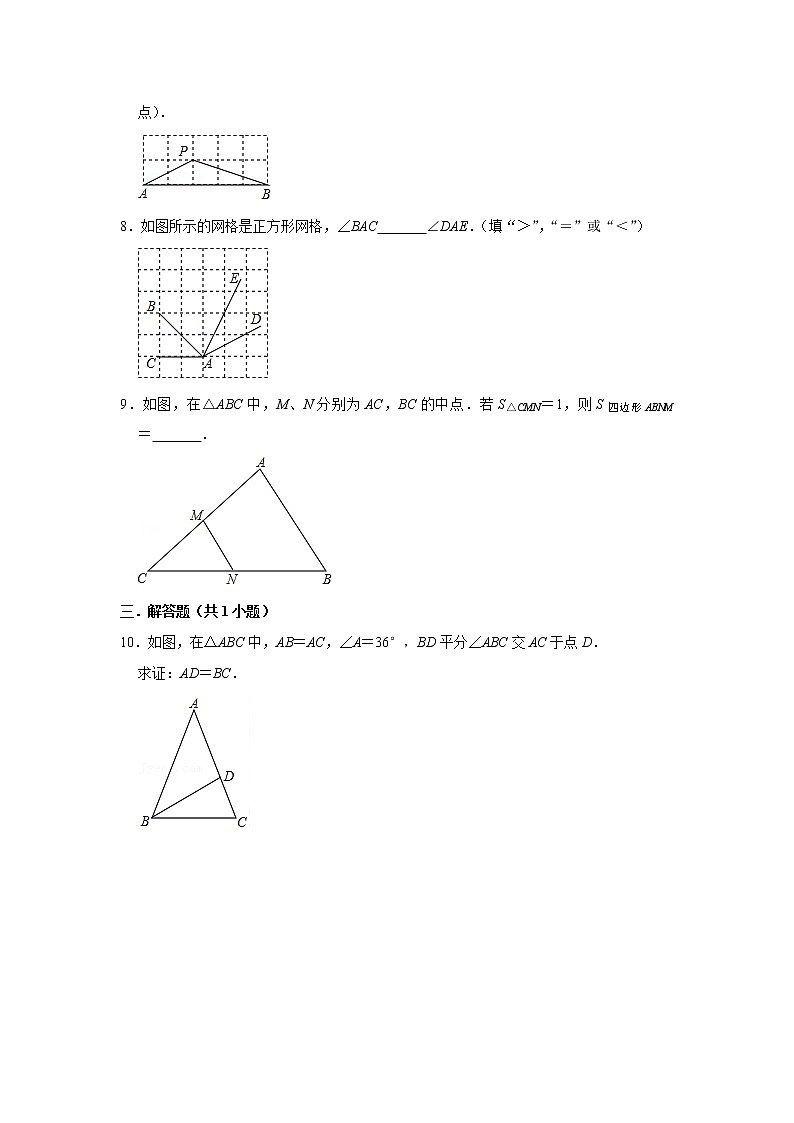
3．如图所示，点P到直线l的距离是（　　）

A．线段PA的长度 B．线段PB的长度
C．线段PC的长度 D．线段PD的长度
二．填空题（共6小题）
4．如图，在△ABC中，AB＝AC，点D在BC上（不与点B，C重合）．只需添加一个条件即可证明△ABD≌△ACD，这个条件可以是 　 　（写出一个即可）．

5．如图所示的网格是正方形网格，A，B，C，D是网格线交点，则△ABC的面积与△ABD的面积的大小关系为：S△ABC　 　S△ABD（填“＞”，“＝”或“＜”）．

6．如图，已知△ABC，通过测量、计算得△ABC的面积约为 　 　cm2．（结果保留一位小数）





7．如图所示的网格是正方形网格，则∠PAB+∠PBA＝　 　°（点A，B，P是网格线交点）．

8．如图所示的网格是正方形网格，∠BAC　 　∠DAE．（填“＞”，“＝”或“＜”）

9．如图，在△ABC中，M、N分别为AC，BC的中点．若S△CMN＝1，则S四边形ABNM＝　 　．

三．解答题（共1小题）
10．如图，在△ABC中，AB＝AC，∠A＝36°，BD平分∠ABC交AC于点D．
求证：AD＝BC．





五年模拟
一．选择题（共11小题）
1．如图，在△ABC中，BC边上的高是（　　）

A．CD B．AE C．AF D．AH
2．一副三角板如图放置，斜边互相平行，且每个三角板的直角顶点都在另一个三角板的斜边上，在图中所标记的角中，与∠1相等的角是（　　）

A．∠2 B．∠3 C．∠4 D．∠5
3．如图，∠B＝43°，∠ADE＝43°，∠AED＝72°，则∠C的度数为（　　）

A．72° B．65° C．50° D．43°
4．如图，AB∥CD，∠A＝100°，∠BCD＝50°，∠ACB的度数为（　　）

A．25° B．30° C．45° D．50°

5．如图，在△ABC中，DE∥BC，若AD＝2，AB＝3，则等于（　　）

A． B． C． D．
6．若相似三角形的相似比为1：4，则面积比为（　　）
A．1：16 B．16：1 C．1：4 D．1：2
7．如图，AB∥CD，EF分别与AB，CD交于点B，F．若∠E＝50°，∠EFC＝110°，则∠A的度数为（　　）

A．20° B．30° C．40° D．50°
8．如图，直线l1∥l2，点A，C，D分别是l1，l2上的点，且CA⊥AD于点A，若∠ACD＝30°，则∠1度数为（　　）

A．30° B．50° C．60° D．70°
9．如图，l1∥l2，点O在直线l1上，将三角板的直角顶点放在点O处，三角板的两条直角边与l2交于A，B两点，若∠1＝35°，则∠2的度数为（　　）

A．35° B．45° C．55° D．65°
10．如图，△ABC中，AB＝AC，AD⊥BC于D，BE⊥AC于E，则以下两个角的关系中不成立的是（　　）

A．∠1＝∠2 B．∠3＝∠2 C．∠4＝∠5 D．∠4＝∠C
11．如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，则sinA的值为（　　）

A． B． C． D．
二．填空题（共29小题）
12．如图所示的网格是正方形网格，点A，B，C是网格线交点，那么∠BAC+∠ACB＝　 　°．







13．利用热气球探测建筑物高度（如图所示），热气球与建筑物的水平距离AD＝100m，则这栋建筑物的高度BC约为　 　m（≈1.4，≈1.7，结果保留整数）．

14．如图，△ABC中，BC＞BA，点D是边BC上的一个动点（点D与点B，C不重合），若再增加一个条件，就能使△ABD与△ABC相似，则这个条件可以是　 　（写出一个即可）．

15．如图，点A，F，C，D在同一条直线上，BC∥EF，AC＝FD，请你添加一个条件　 　，使得△ABC≌△DEF．

16．将一副直角三角板如图摆放，点A落在DE边上，AB∥DF，则∠1＝　 　°．

17．如图所示的网格是正方形网格，A，B，C，D是网格线的交点，那么∠DAC与∠ACB的大小关系为：∠DAC　 　∠ACB（填“＞”，“＝”或“＜”）．

18．将一副三角板如图摆放，斜边AB与直角边DE相交于点F，则∠BFE＝　 　．

19．如图所示的网格是正方形网格，点A，B，C，D是网格线交点，则△ABC的面积与△ADB的面积大小关系为：S△ABC　 　S△ADB（填“＞”“＝”或“＜”）．

20．如图，∠1＝∠2，只需添加一个条件即可证明△ABC≌△BAD，这个条件可以是　 　（写出一个即可）．






21．如图所示的网格是正方形网格，点A，B，C，D，E，F是网格线的交点，则△ABC的面积与△DEF的面积比为　 　．

22．如图，点A，D，B，E在同一条直线上，AD＝BE，AC＝EF，要使△ABC≌△EDF，只需添加一个条件，这个条件可以是　 　．

23．如图，直线l为线段AB的垂直平分线，垂足为C，直线l上的两点E，F位于AB异侧（E，F两点不与点C重合）．只需添加一个条件即可证明△ACE≌△BCF，这个条件可以是　 　．

24．如图，小石同学在A，B两点分别测得某建筑物上条幅两端C，D两点的仰角均为60°，若点O，A，B在同一直线上，A，B两点间距离为3米，则条幅的高CD为　 　米（结果可以保留根号）．

25．如图所示的网格是正方形网格，A，B，C是网格线的交点，则∠ABC与∠ACB的大小关系为：∠ABC　 　∠ACB（填“＞”，“＝”或“＜”）．

26．如图所示，在正方形网格中，点A，B，C，D为网格线的交点，线段AC与BD交于点O，则△ABO的面积与△CDO面积的大小关系为：S△ABO　 　S△CDO（填“＞”，“＝”或“＜”）．

27．如图所示的网格是正方形网格，A，B，C，D是网格线交点，则∠BAC与∠DAC的大小关系为：∠BAC　 　∠DAC（填“＞”，“＝”或“＜”）．

28．如图，AE平分∠CAD，点B在射线AE上，若使△ABC≌△ABD，则还需添加的一个条件是　 　（只填一个即可）．




29．如图所示的网格是正方形网格，则∠BAC+∠CDE＝　 　（点A，B，C，D，E是网格线交点）．

30．如图，在四边形ACBD中，∠ACB＝90°，AB＝AD，E是BD中点，过点E作EF∥AD交AB于点F，连接CF．请写出关于边、角的两条正确结论（不包括已知条件）：
①　 　；
②　 　．

31．如图所示的网格是正方形网格，A，B，C是网格线交点，则∠ABC+∠BAC＝　 　°．

32．如图，在△ABC和△ADC中，AB⊥BC，AD⊥DC，只需添加一个条件即可证明△ABC≌△ADC，这个条件可以是　 　（写出一个即可）．



33．如图所示的网格是正方形网格，A，B，C，D是网格线交点，则△ABO的面积与△CDO的面积的大小关系为：S△ABO　 　S△CDO（填“＞”，“＝”或“＜”）．

34．如图所示，∠MON是放置在正方形网格中的一个角，则tan∠MON的值是　 　．

35．如图所示的网格是正方形网格，A，B，C，D是网格线交点，则△ABC与△DBC面积的大小关系为：S△ABC　 　S△DBC（填“＞”，“＝”或“＜”）．

36．将一副三角板按如图所示的方式放置，则∠1的大小为　 　．







37．如图所示的网格是正方形网格，A，B，C是网格线的交点，D，E是AC，BC分别与网格线的交点，若小正方形的边长为1，则DE的长为　 　．

38．如图，小亮从一盏9米高的路灯下B处向前走了8米到达点C处时，发现自己在地面上的影子CE是2米，则小亮的身高DC为 　 　米．

39．如图所示的正方形网格内，点A，B，C，D，E是网格线交点，那么∠ECD+∠EDC＝　 　°．

40．如图，在△ABC中，D、E分别是AB、AC的中点，若DE＝2cm，则BC＝　 　cm．



三．解答题（共18小题）
41．阅读材料并解决问题：
已知：如图，∠AOB及内部一点P．
求作：经过点P的线段EF，使得点E，F分别在射线OA，OB上，且OE＝OF．
作法：如图．
①以点O为圆心，以任意长为半径作弧，分别交射线OA，OB于点M，N；
②连接NP，作线段NP的垂直平分线，得到线段NP的中点C；
③连接MC并在它的延长线上截取CD＝MC；
④作射线DP，分别交射线OB，OA于点F，E．线段EF就是所求作的线段．
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；

（2）完成下面的证明证明：连接MN．
由②得，线段CN　 　CP（填“＞”，“＝”或“＜”）．
在△MCN和△DCP中，
，
∴△MCN≌△DCP．
∴∠NMC＝∠PDC．
∴MN∥EF（　 　）（填推理的依据）．
又由①得，线段OM＝ON．
可得OE＝OF．



42．已知：如图1，在△ABC中，∠CAB＝60°．求作：射线CP，使得CP∥AB．
下面是小明设计的尺规作图过程．
作法：如图2，
①以点A为圆心，适当长为半径作弧，分别交AC，AB于D，E两点；
②以点C为圆心，AD长为半径作弧，交AC的延长线于点F；
③以点F为圆心，DE长为半径作弧，两弧在∠FCB内部交于点P；
④作射线CP．所以射线CP就是所求作的射线．
根据小明设计的尺规作图过程，
（1）使用直尺和圆规，补全图形；（保留作图痕迹）
（2）完成下面的证明．
证明：连接FP，DE．
∵CF＝AD，CP＝AE，FP＝DE．
∴△ADE≌△　 　，
∴∠DAE＝∠　 　，
∴CP∥AB（　 　）（填推理的依据）．








43．下面是小明同学设计的“作一个角等于已知角的2倍”的尺规作图过程．
已知：∠AOB．
求作：∠ADC，使∠ADC＝2∠AOB．
作法：如图，
①在射线OB上任取一点C；
②作线段OC的垂直平分线，交OA于点D，交OB于点E，连接DC．
所以∠ADC即为所求的角．
根据小明设计的尺规作图过程，
（1）使用直尺和圆规，补全图形（保留作图痕迹）；
（2）完成下面证明（说明：括号里填写作图依据）．
证明：∵DE是线段OC的垂直平分线，
∴OD＝　 　（　 　），
∴∠AOB＝　 　（　 　），
∵∠ADC＝∠AOB+∠DCO，
∴∠ADC＝2∠AOB．











44．已知：如图，点C在∠MON的边OM上．
求作：射线CD，使CD∥ON，且点D在∠MON的角平分线上．
作法：①以点O为圆心，适当长为半径画弧，分别交射线OM，ON于点A，B；②分别以点A，B为圆心，大于的长为半径画弧，交于点Q；③画射线OQ；④以点C为圆心，CO长为半径画弧，交射线OQ于点D；⑤画射线CD．射线CD就是所求作的射线．
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明：
∵OD平分∠MON，
∴∠MOD＝　 　．
∵OC＝CD，
∴∠MOD＝　 　．
∴∠NOD＝∠CDO．
∴CD∥ON（　 　）（填推理的依据）．












45．已知：直线l和l外一点P．求作：直线l的垂线，使它经过点P．
作法：①在直线l上任取两点A、B；
②分别以点A、B为圆心，AP，BP长为半径作弧，在直线l下方两弧交于点C；③作直线PC．所以直线PC为所求作的垂线．
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明．
证明：连结AP、AC、BP、BC．
∵AP＝AC，BP＝BC，AB＝AB，
∴△APB≌△ACB　 　（填推理依据）．
∴∠PAB＝∠CAB，
∴PC⊥AB　 　（填推理依据）．
















46．如图，在△ABC中，点D是线段AB的中点．
求作：线段DE，使得点E在线段AC上，且DE＝BC．
作法：①分别以点A，C为圆心，大于AC长为半径作弧，两弧相交于点M，N两点；
②作直线MN，交AC于点E；
③连接DE．
所以线段DE即为所求的线段．
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明．
证明：∵AM＝CM，AN＝CN，
∴MN是AC的垂直平分线（　 　）．（填推理的依据）
∴点E是AC的中点．
∵点D是AB的中点，
∴DE＝BC（　 　）．（填推理的依据）













47．如图，在Rt△ABC中，∠C＝90°．
求作：线段CD，使得点D在线段AB上，且CD＝AB．
作法：①分别以点A，B为圆心，大于AB长为半径作弧，两弧相交于点M，N两点；
②作直线MN，交AB于点D；
③连接CD．
所以线段CD即为所求的线段．
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明．
证明：∵AM＝BM，AN＝BN，
∴MN是AB的垂直平分线（ 　 　）．（填推理的依据）
∴点D是AB的中点．
∵∠C＝90°
∴CD＝AB（ 　 　）．（填推理的依据）













48．下面是小玲同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程．
已知：如图1，直线l和直线l外一点P．求作：直线PM，使直线PM∥直线l．
作法：如图2，
①在直线l上任取一点A，作射线AP；
②以P为圆心，PA为半径作弧，交直线l于点B，
连接PB；
③以P为圆心，PB长为半径作弧，交射线AP于点C；分别以B，C为圆心，大于长为半径作弧，
在AC的右侧两弧交于点M；
④作直线PM；
所以直线PM就是所求作的直线．
根据上述作图过程，回答问题：
（1）用直尺和圆规，补全图2中的图形；
（2）完成下面的证明：
证明：由作图可知PM平分∠CPB，
∴∠CPM＝∠　 　＝∠CPB．
又∵PA＝PB，
∴∠PAB＝∠PBA．（　 　）（填依据）．
∵∠CPB＝∠PAB+∠PBA，
∴∠PAB＝∠PBA＝∠CPB．
∴∠CPM＝∠PAB．
∴直线PM∥直线l．（　 　）（填依据）．








49．已知：如图Rt△ABC中，∠ACB＝90°．
求作：点P，使得点P在AC上，且点P到AB的距离等于PC．
作法：
①以点B为圆心，以任意长为半径作弧，分别交射线BA，BC于点D，E；
②分别以点D，E为圆心，以大于DE的长为半径作弧，两弧在∠ABC内部交于点F；
③作射线BF交AC于点P．
则点P即为所求．
（1）使用直尺和圆规，补全图形（保留作图痕迹）；
（2）完成下面证明
证明：连接DF，FE
在△BDF和△BEF中，
，
∴△BDF≌△BEF．
∴∠ABF＝∠CBF（　 　）（填推理的依据）．
∵∠ACB＝90°，点P在AC上，
∴PC⊥BC．
作PQ⊥AB于点Q．
∵点P在BF上，
∴PC＝　 　（　 　）（填推理的依据）．





50．已知，如图，△ABC是等边三角形，BD⊥AC于D，E是BC延长线上的一点，DB＝DE．求∠E的度数．

51．如图，在等腰△ABC中，AB＝AC，直线l过点A．点B与点D关于直线l对称，连接AD，CD．求证：∠ACD＝∠ADC．

52．已知：如图，在△ABC和△DEF中，点B、E、C、F四点在一条直线上，且BE＝CF，AB＝DE，∠B＝∠DEF．
求证：△ABC≌△DEF．

53．已知：如图，AB与CD交于点E，点E是线段AB的中点，∠A＝∠B．求证：AC＝BD．



54．如图，AB＝AD，AC＝AE，∠BAE＝∠DAC．求证：∠C＝∠E．

55．如图，C为∠AOB平分线上一点，CD∥OB交OA于点D．
求证：OD＝CD．

56．如图，AB＝AD，∠BAC＝∠DAC，∠D＝70°，求∠B的度数．

57．已知：如图，AB＝DE，AF＝DC，请补充一个条件可以得到BC＝EF．
补充的条件：　 　．






58．如图，点B，E，C，F在一条直线上，AB∥DE，AB＝DE，BE＝CF．求证：∠A＝∠D．