2022届高考数学模拟试题 全国甲卷（理数）（含答案）

这是一份2022届高考数学模拟试题 全国甲卷（理数）（含答案），共13页。
2022届高考数学各省模拟试题汇编卷全国甲卷（理数）【满分：150分】一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。1.（2022 四川绵阳适应考试）设集合，，则为(   )A. B. C. D.2.（2022 贵州仁怀模拟考试）设，则z的共轭复数对应的点在(   )A.第一象限 B.第二象限 C.第三象限 D.第四象限3.（2022 黔东南州模拟考试）设，，则(   )A. B. C. D.4.（2022 广西省原创模拟）《九章算术》是我国古代内容极其丰富的数学名著，书中有如下问题：“今有委菽依垣内角，下周三丈，高七尺，问积及为菽几何？”其意思为：“靠墙壁堆放大豆成半圆锥形，大豆堆底面的弧长为3丈，高为7尺，问大豆堆体积和堆放的大豆有多少斛？”已知1斛大豆=2.43立方尺，1丈=10尺，圆周率约为3，估算出堆放的大豆有(   )A.140斛 B.142斛 C.144斛 D.146斛5.（2022 广西桂平三中联考）在中，，，D为AB中点，的面积为，则AC等于(   )A.2 B. C. D.6.（2022 广西省联考）已知正项等比数列中，公比，前n项和为，若，，则(   )A.127 B.128 C.255 D.2567.（2022 四川遂宁诊断考试）如图，在中，D为线段上异于的任意一点，E为的中点，若，则(    )A.     B.     C.     D.8.（2022 贵州省模拟联考）已知函数是定义在R上的奇函数，且，若，则(   )
A.   B.   C.   D.9.（2022 西藏拉萨模拟考试）已知分别为双曲线的左、右焦点，点是其一条渐近线上一点，且以为直径的圆经过点，若的面积为，则双曲线的离心率为(  )A.   B.2  C.        D.3 10.（2022 贵州遵义模拟考试）将函数的图象向右平移个单位后得到函数的图象，则下列说法错误的是(    )A．的图象的一条对称轴为B．在上单调递增C．在上的最大值为D．的一个零点为11.（2022 云南统一监测考试）三棱锥的顶点都在球O的球面上，，，.若三棱锥的体积的最大值为，则球O的体积为(   )
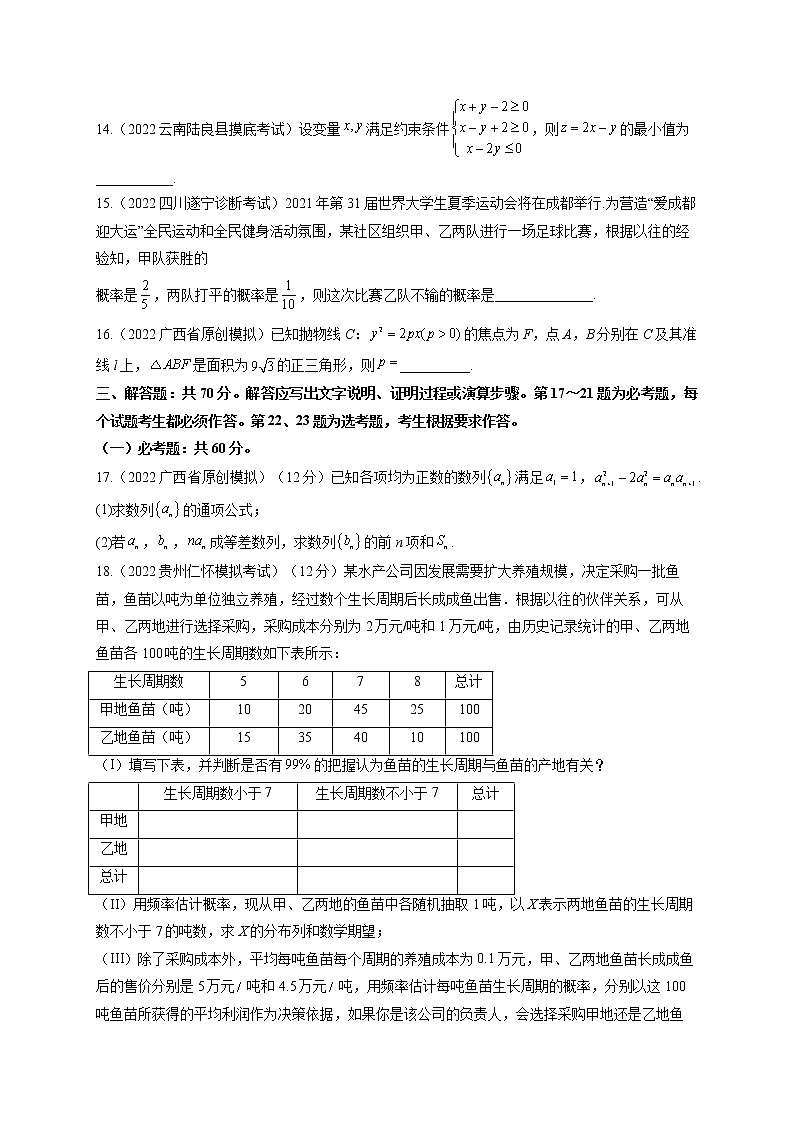
A. B. C. D.12.（2022 云南昆明三诊一模）已知函数，若有四个不同的零点，则a的取值范围为(   )A. B. C. D.二、填空题：本题共4小题，每小题5分，共20分。13.（2022 四川绵阳适应考试）已知幂函数的图象过点，则________.14.（2022 云南陆良县摸底考试）设变量满足约束条件，则的最小值为___________.15.（2022 四川遂宁诊断考试）2021年第31届世界大学生夏季运动会将在成都举行.为营造“爱成都迎大运”全民运动和全民健身活动氛围，某社区组织甲、乙两队进行一场足球比赛，根据以往的经验知，甲队获胜的概率是，两队打平的概率是，则这次比赛乙队不输的概率是______________.16.（2022 广西省原创模拟）已知抛物线C：的焦点为F，点A，B分别在C及其准线l上，是面积为的正三角形，则__________.三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17～21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。（一）必考题：共60分。17.（2022 广西省原创模拟）（12分）已知各项均为正数的数列满足，.(1)求数列的通项公式；(2)若，，成等差数列，求数列的前n项和.18.（2022 贵州仁怀模拟考试）（12分）某水产公司因发展需要扩大养殖规模，决定采购一批鱼苗，鱼苗以吨为单位独立养殖，经过数个生长周期后长成成鱼出售．根据以往的伙伴关系，可从甲、乙两地进行选择采购，采购成本分别为2万元/吨和1万元/吨，由历史记录统计的甲、乙两地鱼苗各100吨的生长周期数如下表所示：生长周期数5678总计甲地鱼苗（吨）10204525100乙地鱼苗（吨）15354010100（I）填写下表，并判断是否有的把握认为鱼苗的生长周期与鱼苗的产地有关？ 生长周期数小于7生长周期数不小于7总计甲地   乙地   总计   （II）用频率估计概率，现从甲、乙两地的鱼苗中各随机抽取1吨，以X表示两地鱼苗的生长周期数不小于7的吨数，求X的分布列和数学期望；（III）除了采购成本外，平均每吨鱼苗每个周期的养殖成本为0.1万元，甲、乙两地鱼苗长成成鱼后的售价分别是5万元吨和4.5万元吨，用频率估计每吨鱼苗生长周期的概率，分别以这100吨鱼苗所获得的平均利润作为决策依据，如果你是该公司的负责人，会选择采购甲地还是乙地鱼苗？参考公式：，其中．0.0500.0100.001k3.8416.63510.82819.（2022 云南红河统一检测）（12分）如图，在多边形中（图1）．四边形为长方形，为正三角形，，，现以为折痕将折起，使点P在平面内的射影恰好是的中点（图2）．（1）证明：平面：（2）若点E在线段上，且，求二面角的余弦值．20.（2022 广西桂平三中联考）（12分）已知函数（且）.（1）求函数的单调区间；（2）当时，求证：对任意，恒成立.21.（2022 四川内江零模考试）（12分）已知是椭圆上的两点．（1）若直线的斜率为1，求弦长的最大值；（2）设线段的垂直平分线与轴交于点，求的取值范围．（二）选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。22.（2022 四川眉山诊断性考试）（10分）[选修4 – 4：坐标系与参数方程]已知曲线C的参数方程为（为参数），以平面直角坐标系的原点为极点，x的正半轴为极轴建立极坐标系．（1）求曲线C的极坐标方程；（2）是曲线C上两点，若，求的值．23.（2022 西藏山南模拟考试）（10分）[选修4 – 5：不等式选讲]已知函数.（1）求不等式的解集；（2）若的最小值为k，且实数，满足，求证：
答案以及解析1.答案：C解析：因为，所以.因为且，所以所以.故C正确.2.答案：D解析：由，得，所以，对应的点在第四象限.故选D.3.答案：D解析：所以.4.答案：C解析：由题意可知，半圆锥的体积为(立方尺)，所以大豆有(斛)，故选C.5.答案：B解析：在中，，所以，由余弦定理，可得，故选：B.6.答案：C解析：，，且，，，故选：C.7.答案：B解析：由图可知，点B、D、C三点共线，所以，因为E为AD中点，所以，所以，所以，因为，所以，所以.故选B.8.答案：C解析：9.答案：B解析：设为上第一象限内的点，以为直径的圆的方程为，解得，即，所以，， 10.答案：A解析：则，对选项A，因为，故A错误；对选项B，因为解得所以在上单调递增，故B正确；对选项C，因为，所以，所以，，，故C正确；对选项D，，故D正确.11.答案：D解析：12.答案：A解析：13.答案：3解析：幂函数的图象经过点，；解得.故，则，故答案为：3.14.答案：-2解析：如图所示：画出可行域和目标函数，根据图像知：当时，有最小值为-2.故答案为：-2.15.答案：解析：设事件A为“这次比赛乙队不输”，事件B为“这次比赛乙队获胜”，事件C为“这次比赛甲、乙两队打半”，所以，所以这次比赛乙队不输的概率.16.答案：3解析：如图所示，因为是正三角形，所以，由抛物线的定义可知，，过F作，又知，所以，所以，则.由的面积为可知，，所以.17.答案：(1)(2)解析：解：(1)由，得，
即，又，所以.
又知，所以是以1为首项，2为公比的等比数列，
故数列的通项公式为.(2)由，，成等差数列可知，，
所以.
所以，①，②由①-②，得

.
故.18.答案：（Ⅰ） 生长周期数小于7生长周期数不小于7总计甲地3070100乙地5050100总计80120200有的把握认为鱼苗的生长周期与鱼苗的产地有关（Ⅱ）X012P（Ⅲ）略解析：（Ⅰ）补充完整的列联表如下所示： 生长周期数小于7生长周期数不小于7总计甲地3070100乙地5050100总计80120200所以，所以有的把握认为鱼苗的生长周期与鱼苗的产地有关；（Ⅱ）由题可知，甲地鱼苗生长周期数小于7的吨数占，生长周期数不小于7的吨数占；乙地鱼苗生长周期数小于7的吨数占，生长周期数不小于7的吨数占，所以X的可能取值为0，1，2，，，，所以X的分布列为：X012P所以．19.答案：（1）见解析（2）解析：（1）作的中点，连接，由题知平面．因为，所以，又因为，所以平面．（2）取的中点，连接，则，，，以为坐标原点，以，，分别为、轴的正方向建立空间直角坐标系．则，，，，，设平面的一个法向量为则有，令，所以易知平面的一个法向量为所以，所以二面角的余弦值为．20.答案：（1）函数的单调递增区间为，单调递减区间为（2）见解析解析：（1）.
若，令，则，，解得，令，解得；
若，令，则，，解得，令，解得，综上所述，函数的单调递增区间为，单调递减区间为.（2），，.（*）
当时，不等式（*）两边取对数，则.
记函数，则.
令，解得，令，解得，
则在上单调递增，在上单调递减，
.
令函数，则，
令，解得，令，解得，
则在上单调递减，在上单调递增，又，，
当时，恒成立，恒成立，
当时，对任意，恒成立.21.答案：解：（1）设直线的方程为，、，由，得，由得．，，所以，易知当时，取得最大值．（2）设、，的中点，①若直线平行于轴，则线段的垂直平分线为轴，故，②若直线不平行于轴，因为线段的垂直平分线与轴相交，所以直线不平行于轴，即，由，两式相减整理，设是的中点，∴，因此又∵，且∴，即．解得．由或知或．综上，的取值范围是．22.答案：（1）由（为参数），得曲线的普通方程为，将，代入，得，即，所以曲线的极坐标方程为.（2）由（1）知，设点的极坐标为，因为，则点的极坐标为，所以．23.答案：（1）①当时，不等式即为，解得；②当时，不等式即为，；③当时，不等式即为，.综上，不等式的解集为.（2）由绝对值不等式的性质可得：当时，取最小值4，即，即当且仅当时等号成立.