中考平行四边形与多边形课件PPT

这是一份中考平行四边形与多边形课件PPT，共11页。

1、多边形内角和 （n﹣2）•180°，其中n≥3且n为整数。（1）推导方法：从n边形的一个顶点出发，引出（n﹣3）条对角线，将n边形分割为（n﹣2）个三角形，则（n﹣2）个三角形的所有内角之和就是n边形的内角和。（2）思想方法：将多边形转化为三角形。n边形共有几条对角线 2、多边形外角和等于360°。（1）多边形的外角：每个顶点处取一个外角，则n边形取n个外角。
正n边形有几条对称轴当n为奇数时，是轴对称图形，不是中心对称图形当n为偶数时，既是轴对称图形，又是中心对称图形
1．（2021•襄阳中考）多边形的每一个外角等于60°，这个多边形的边数是（　　）A．3B．6C．9D．122．（2021•福建中考）如图，点F在正五边形ABCDE的内部，△ABF为等边三角形，则∠AFC等于（　　）
A．108°B．120°C．126°D．132°
3．（2021•扬州中考）如图，点A、B、C、D、E在同一平面内，连接AB、BC、CD、DE、EA，若∠BCD＝100°，则∠A+∠B+∠D+∠E＝（　　）A．220°B．240°C．260°D．280°4．（2021•株洲中考）如图所示，在正六边形ABCDEF内，以AB为边作正五边形ABGHI，则∠FAI＝（　　）
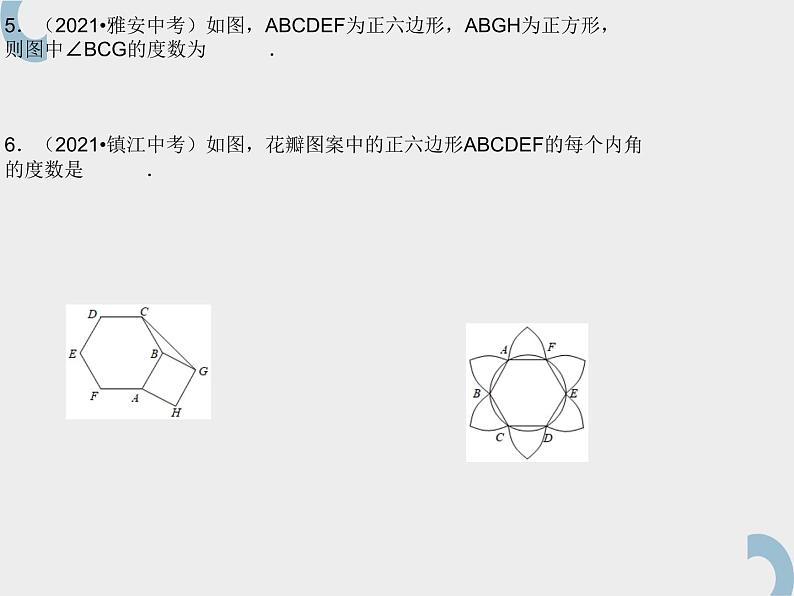
5．（2021•雅安中考）如图，ABCDEF为正六边形，ABGH为正方形，则图中∠BCG的度数为 　 　．6．（2021•镇江中考）如图，花瓣图案中的正六边形ABCDEF的每个内角的度数是 　 　．
考点02 平行四边形的性质与判定
1、平行四边形的性质：（1）平行四边形的对边平行且相等。（2）平行四边形的对角相等。（3）平行四边形的对角线互相平分。（4）平行四边形的面积：①平行四边形的面积等于它的底和这个底上的高的乘积②同底（等底）同高（等高）的平行四边形面积相等。。
（1）两组对边分别平行的四边形是平行四边形。（2）两组对边分别相等的四边形是平行四边形。（3）一组对边平行且相等的四边形是平行四边形。（4）两组对角分别相等的四边形是平行四边形。（5）对角线互相平分的四边形是平行四边形。
7．（2021•滨州中考）如图，在▱ABCD中，BE平分∠ABC交DC于点E．若∠A＝60°，则∠DEB的大小为（　　）A．130°B．125°C．120°D．115°8．（2021•贵阳中考）如图，在▱ABCD中，∠ABC的平分线交AD于点E，∠BCD的平分线交AD于点F，若AB＝3，AD＝4，则EF的长是（　　）A．1B．2C．2.5D．39．（2021•苏州中考）如图，在平行四边形ABCD中，将△ABC沿着AC所在的直线折叠得到△AB′C，B′C交AD于点E，连接B′D，若∠B＝60°，∠ACB＝45°，AC＝，则B′D的长是（　　）
10．（2021•天津中考）如图，▱ABCD的顶点A，B，C的坐标分别是（0，1），（﹣2，﹣2），（2，﹣2），则顶点D的坐标是（　　）A．（﹣4，1）B．（4，﹣2）C．（4，1）D．（2，1）11．（2020•衡阳中考）如图，在四边形ABCD中，对角线AC和BD相交于点O，下列条件不能判断四边形ABCD是平行四边形的是（　　）A．AB∥DC，AD∥BCB．AB＝DC，AD＝BCC．AB∥DC，AD＝BCD．OA＝OC，OB＝OD
13．（2021•湘潭中考）如图，在▱ABCD中，对角线AC，BD相交于点O，点E是边AB的中点 已知BC＝10，则OE＝　 　．14．（2021•江西中考）如图，将▱ABCD沿对角线AC翻折，点B落在点E处，CE交AD于点F，若∠B＝80°，∠ACE＝2∠ECD，FC＝a，FD＝b，则▱ABCD的周长为 　 　．