2022年中考数学一轮复习平面直角坐标系与函数考点精讲精练课件

这是一份2022年中考数学一轮复习平面直角坐标系与函数考点精讲精练课件，共34页。PPT课件主要包含了考点梳理，原点重合，a－b，－ab，－a－b，2m－ab，a2m－b，y2－y1，x2－x1，坐标系中点坐标的平移等内容，欢迎下载使用。

考点1 平面直角坐标系的概念及点的坐标特征
在平面内画两条互相_______、___________的数轴，组成平面直角坐标系．水平的数轴称为x轴或横轴，竖直的数轴称为y轴或纵轴
①若点P(a，b)在第一象限，则a>0，b>0；②若点P(a，b)在第二象限，则a____0，b____0；③若点P(a，b)在第三象限，则a____0，b____0；④若点P(a，b)在第四象限，则a____0，b____0
与坐标轴有关的点的坐标特征
①若点P(a，b)在x轴上，则b＝____；②若点P(a，b)在y轴上，则a＝____；③若点P(a，b)是原点，则a＝____且b＝____；④平行于x轴的直线上的点的_____坐标相同，平行于y轴的直线上的点的_____坐标相同
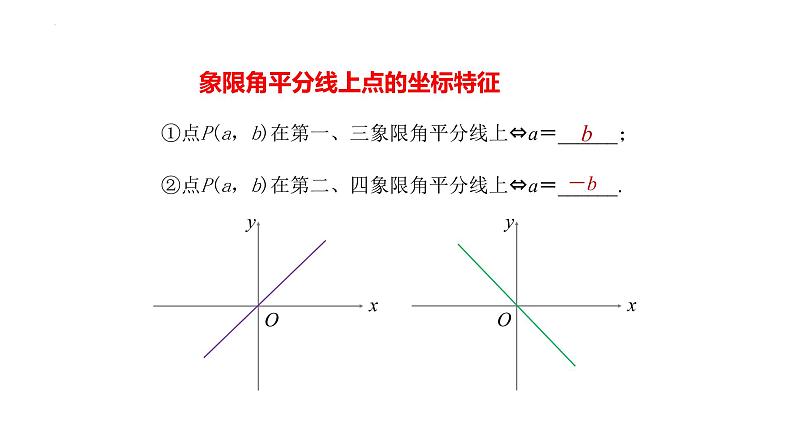
象限角平分线上点的坐标特征
①点P(a，b)在第一、三象限角平分线上⇔a＝______；
②点P(a，b)在第二、四象限角平分线上⇔a＝______.
①点P(a，b)关于x轴对称点P1的坐标为___________；②点P(a，b)关于y轴对称点P2的坐标为___________；③点P(a，b)关于原点对称点P3的坐标为_____________；④点P(a，b)关于直线x＝m的对称点P4的坐标为_____________；⑤点P(a，b)关于直线y＝m的对称点P5的坐标为_____________.
①关于坐标轴对称，关于谁对称谁不变，另一个变号；②关于原点对称，互为相反数
简记为“右加左减，上加下减”.
1．(2021春·江西赣州期末)如果a是任意实数，则点P(a－2，a＋1)一定不可能在( )A．第一象限 B．第二象限C．第三象限 D．第四象限
2．(江西上饶校级期末)若点P是平面直角坐标系中第二象限内的点，且点P到x轴的距离是2，到y轴的距离是3，则点P的坐标是( )A．(－2，3) B．(2，－3)C．(－3，2) D．(3，－2)
3．(2021·成都)在平面直角坐标系xOy中，点M(－4，2)关于x轴对称的点的坐标是( )A．(－4，2) B．(4，2)C．(－4，－2) D．(4，－2)
横坐标不变，纵坐标变为相反数
4．在平面直角坐标系中，点(3，2)关于原点对称的点的坐标是( )A．(2，3) B．(－3，2)C．(－3，－2) D．(－2，－3)
横、纵坐标均变为相反数
5．(2020·江西南昌模拟)已知点M(2x－3，3－x)，在第一、三象限的角平分线上，则M点的坐标为___________．
2x－3 = 3－x=1
6．(2021·西宁)在平面直角坐标系xOy中，点A的坐标是(2，－1)，若AB∥y轴，且AB＝9，则点B的坐标是______________________．
(2，8)或(2，－10)
考点2 函数的相关概念
在变化过程中，有两个变量x和y，如果对于x在某一范围内的每一个确定的值，y都有___________确定的值与它对应，那么y就是x的函数
常量、变量及函数的定义
函数的表示方法及其图象
表示方法：1.解析式法；2.列表法；3._____________
图象的画法：1.列表；2.___________；3.连线
7．下列各图能表示y是x的函数是( )
对于x在某一范围内的每一个确定的值，y都有唯一确定的值与它对应
易错提醒： π是常量.
例1. 一天，小亮看到家中的塑料桶中有一个竖直放置的玻璃杯，桶子和杯子的形状都是圆柱形，桶口的半径是杯口半径的2倍，其主视图如图所示．小亮决定做个试验：把塑料桶和玻璃杯看作一个容器，对准杯口匀速注水，注水过程中杯子始终竖直放置，则下列能反映容器最高水位h与注水时间t之间关系的大致图象是( )
(1)认真观察几何图形，找出运动起点和终点，由动点移动范围确定自变量取值范围；(2)分清整个运动过程分为几段，关注动点运动过程中的特殊位置(即拐点)时的函数值．常关注的拐点包括运动起点和终点时的函数值，和最大(小)函数值；(3)关注每一段运动过程中函数值的变化规律，与图象上升(或下降)的变化趋势相比对；(4)在以上排除法行不通的情况下，需要写出各段的函数解析式，进行选择．
判断含动点图形的函数图象
1．(2021·青海)新龟兔赛跑的故事：龟兔从同一地点同时出发后，兔子很快把乌龟远远甩在后头．骄傲自满的兔子觉得自己遥遥领先，就躺在路边呼呼大睡起来．当它一觉醒来，发现乌龟已经超过它，于是奋力直追，最后同时到达终点．用S1，S2分别表示乌龟和兔子赛跑的路程，t为赛跑时间，则下列图象中与故事情节相吻合的是( )
2．(2021·南通)如图，四边形ABCD中，AB∥DC，DE⊥AB，CF⊥AB，垂足分别为E，F，且AE＝EF＝FB＝5 cm，DE＝12 cm.动点P，Q均以1 cm/s的速度同时从点A出发，其中点P沿折线AD－DC－CB运动到点B停止，点Q沿AB运动到点B停止，设运动时间为t(s)，△APQ的面积为y(cm2)，则y与t对应关系的图象大致是( )
例二 根据图象分析、判断实际问题
例2. (2021·资阳)一对变量满足如图的函数关系．设计以下问题情境：①小明从家骑车以600米/分的速度匀速骑了2.5分钟，在原地停留了2分钟，然后以1000米/分的速度匀速骑回家．设所用时间为x分钟，离家的距离为y千米；②有一个容积为1.5升的开口空瓶，小张以0.6升/秒的速度匀速向这个空瓶注水，注满后停止，等2秒后，再以1升/秒的速度匀速倒空瓶中的水．设所用时间为x秒，瓶内水的体积为y升；③在矩形ABCD中，AB＝2，BC＝1.5，点P从点A出发．沿AC→CD→DA路线运动至点A停止．设点P的运动路程为x，△ABP的面积为y.其中，符合图中函数关系的情境个数为( )A．3 B．2 C．1 D．0
①找特殊点，即起点、终点、交点或转折点，说明图象在此点处的状态或变化；②若有两个函数时，各个分段图象中，图象在上面的函数值大于图象在下面的函数值；③分析图象的过程中，注意找准自变量所对应的阶段．
分析实际问题的函数图象
3．(2021·邵阳)某天早晨7：00，小明从家骑自行车去上学，途中因自行车发生故障，就地修车耽误了一段时间，修好车后继续骑行，7：30赶到了学校．如图所示的函数图象反映了他骑车上学的整个过程．结合图象，判断下列结论正确的是( )A．小明修车花了15 minB．小明家距离学校1100 mC．小明修好车后花了30 min到达学校D．小明修好车后骑行到学校的平均速度是3 m/s
4．(2021·牡丹江)春耕期间，市农资公司连续8天调进一批化肥，并在开始调进化肥的第七天开始销售．若进货期间每天调进化肥的吨数与销售期间每天销售化肥的吨数都保持不变，这个公司的化肥存量s(单位：吨)与时间t(单位：天)之间的函数关系如图所示，则该公司这次化肥销售活动(从开始进货到销售完毕)所用的时间是______天．
每天销售的-每天调进的化肥吨数：
(30-20)÷(8-6)=5(吨)
最后20吨化肥销售的天数：
这次化肥销售活动所用的时间是8+2=10(天)
1．(2021春·江西赣州期末)如图，坐标平面上有P，Q两点，其坐标分别为(5，a)，(b，7)，根据图中P，Q两点的位置，则点(6－b，a－10)在( )A．第一象限 B．第二象限C．第三象限 D．第四象限
2．(2021·广西)如图是某市一天的气温随时间变化的情况，下列说法正确的是( )A．这一天最低温度是－4℃B．这一天12时温度最高C．最高温比最低温高8℃D．0时至8时气温呈下降趋势
3．(2021·海南)李叔叔开车上班，最初以某一速度匀速行驶，中途停车加油耽误了几分钟，为了按时到单位，李叔叔在不违反交通规则的前提下加快了速度，仍保持匀速行驶，则汽车行驶的路程y(千米)与行驶的时间t(小时)的函数关系的大致图象是( )
5．(2021·扬州)在平面直角坐标系中，若点P(1－m，5－2m)在第二象限，则整数m的值为_________．
6．(2021·上海)某人购进一批苹果到集贸市场零售，已知卖出的苹果数量与售价之间的关系如图所示，成本5元/千克，现以8元卖出，挣得__________元．
中考失分点专练：点的坐标弄错或弄反
1．平面直角坐标系中，点P(－2，3)关于x轴对称的点的坐标为( )A．(－2，－3) B．(2，－3)C．(－3，－2) D．(3，－2)
2．若点P在第二象限，且P点到x轴的距离为3，到y轴的距离为2，则P点坐标为( )A．(－3，2) B．(－2，3)C．(3，－2) D．(2，－3)