

- 专题18.12 《平行四边形》全章复习与巩固(专项练习)-2021-2022学年八年级数学下册基础知识专项讲练(人教版) 试卷 0 次下载
- 专题18.13 《平行四边形》之几何模型-将军饮马(知识讲解)-2021-2022学年八年级数学下册基础知识专项讲练(人教版)学案 学案 0 次下载
- 专题18.15 平行四边形-面积问题(专项练习)-2021-2022学年八年级数学下册基础知识专项讲练(人教版) 试卷 0 次下载
- 专题18.16 平行四边形-存在性问题(专项练习)-2021-2022学年八年级数学下册基础知识专项讲练(人教版) 试卷 0 次下载
- 专题18.17 直角三角形斜边上的中线(专项练习)-2021-2022学年八年级数学下册基础知识专项讲练(人教版) 试卷 1 次下载
专题18.14 《平行四边形》之几何模型-将军饮马(专项练习)-2021-2022学年八年级数学下册基础知识专项讲练(人教版)
展开专题18.14 《平行四边形》之几何模型-将军饮马(专项练习)
一、单选题
1.(2020·湖北黄冈市·八年级期末)如图,正方形 中,, 是 的中点,点 是对角线 上一动点,则 的最小值为( )
A.4 B. C. D.
2.(2020·华南师大(广东)教育文化传播有限公司八年级月考)如图,在正方形ABCD中,E是AB上一点,BE=2,AE=4,P是AC上一动点,则PB+PE的最小值是( )
A.6 B.2 C.8 D.2
3.(2020·四川攀枝花市·攀枝花第二初级中学八年级月考)如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A.2 B.4 C.8 D.16
4.(2020·湖北孝感市·九年级月考)如图,已知正方形的边长为,点分别是边上的动点,满足则的最小值为( )
A. B. C. D.
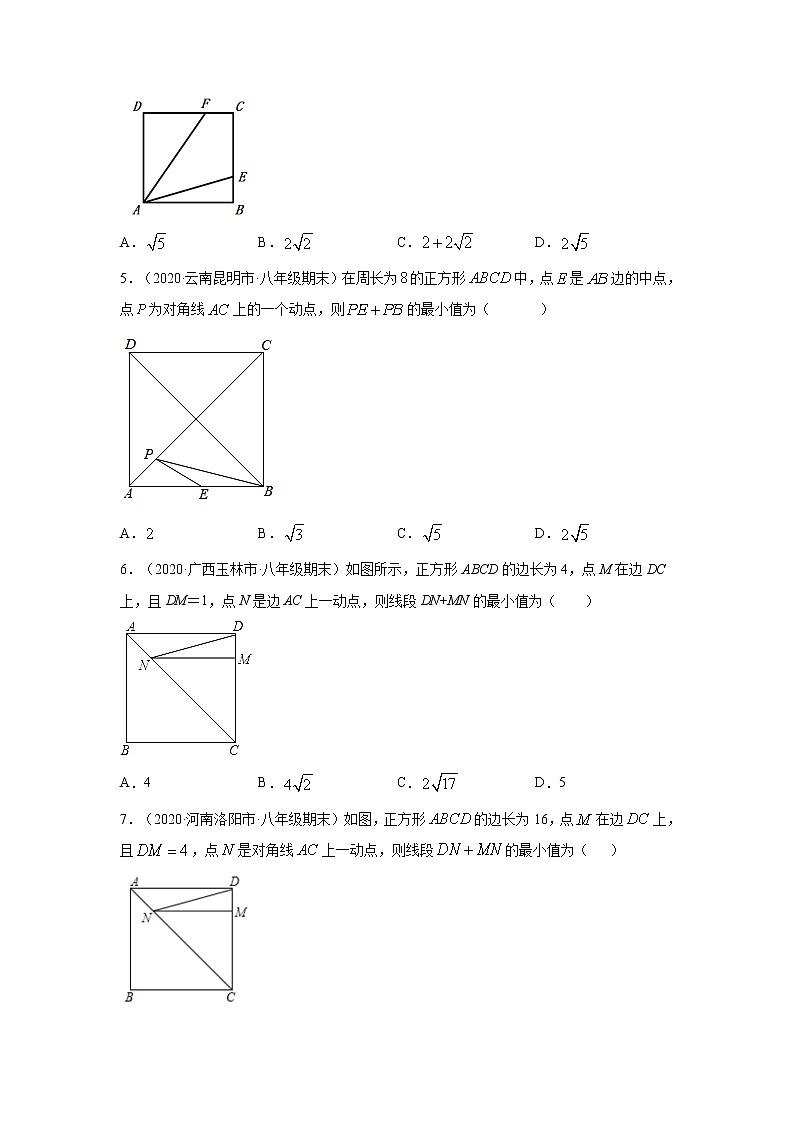
5.(2020·云南昆明市·八年级期末)在周长为的正方形中,点是边的中点,点为对角线上的一个动点,则的最小值为( )
A. B. C. D.
6.(2020·广西玉林市·八年级期末)如图所示,正方形ABCD的边长为4,点M在边DC上,且DM=1,点N是边AC上一动点,则线段DN+MN的最小值为( )
A.4 B. C. D.5
7.(2020·河南洛阳市·八年级期末)如图,正方形的边长为16,点在边上,且,点是对角线上一动点,则线段的最小值为( )
A.16 B. C.20 D.
8.(2020·甘肃天水市·八年级期末)如图,菱形ABCD的边长是2,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
A. B.
C.2 D.
9.(2019·南通市通州区实验中学八年级期中)如图,正方形的面积为12,是等边三角形,点在正方形内,在对角线上有一点,使最小,则图中长度等于这个最小值的线段共有( )条.
A.5 B.6 C.7 D.8
10.(2019·洛阳市实验中学八年级月考)如图,正方形ABCD的面积为2,E、F为AB、BC中点,P为AC上的动点,的最小值等于( )
A. B.2 C. D.
11.(2020·太原市志达中学校八年级月考)如图,在矩形中,,,点若为的中点,点为上任意一点,周长的最小值为( )
A. B. C. D.
12.(2020·焦作市实验中学九年级月考)如图,在边长为6的菱形ABCD中,∠DAB=60°,E为AB的中点,F是AC上的一动点,则EF+BF的最小值为( )
A.6 B.3 C.3 D.3
13.(2020·浙江台州市·九年级期中)如图,在菱形中, , , ,的半径分别为2和1, , ,分别是边、和上的动点,则的最小值是( )
A. B.2 C.3 D.
14.(2020·石家庄精英中学九年级月考)如图,在菱形中,,点是的中点,是对角线上的一个动点,若的最小值是9,则的长是( )
A. B. C.9 D.4.5
15.(2021·全国九年级专题练习)如图,动点在边长为2的正方形内,且,是边上的一个动点,是边的中点,则线段的最小值为( )
A. B. C. D.
16.(2020·安徽安庆市·八年级期末)已知菱形ABCD的面积为8,对角线AC的长为4,∠BCD=60°,M为BC的中点,若P为对角线AC上一动点,则PB+PM的最小值为( )
A. B.2 C.2 D.4
17.(2020·安徽合肥市·八年级期末)如图,在矩形ABCD中,AB=3,BC=4,在矩形内部有一动点P满足S△PAB=3S△PCD,则动点P到点A,B两点距离之和PA+PB的最小值为( )
A.5 B. C. D.
18.(2020·陕西省榆林市第一中学分校九年级月考)如图所示,四边形OABC为正方形,边长为6,点A,C分别在x轴,y轴的正半轴上,点D在OA上,且D的坐标为(2,0),P是OB上的动点,试求PD+PA和的最小值是( )
A.2 B. C.2 D.6
19.(2020·湖北武汉市·八年级开学考试)如图,在矩形中,,,为矩形内一点,连接,,,则的最小值是( )
A. B. C. D.
20.(2020·高州市第八中学九年级月考)如图,已知正方形ABCD的边长为4,P是对角线BD上一点,于点E,于点F,连接AP,给出下列结论:①;②四边形PECF的周长为8;③一定是等腰三角形;④;⑤的最小值为其中正确结论的序号为( )
A.①②④⑤ B.①③④⑤ C.②④⑤ D.②③⑤
二、填空题
21.(2020·黑龙江牡丹江市·八年级期末)如图所示,矩形中,,将矩形沿直线折叠,使直线两侧的部分能够完全重合,点在边上,且,在直线上有一个动点,连接,则周长的最小值是______.
22.(2020·重庆八年级月考)如图,四边形ABCD中,AB=BC=3,∠A=∠C=90°,∠ABC=120°,点E是对角线BD上的一个动点,过点E分别作AB,BC,CD,AD的垂线,垂足分别为点F,H,I,G,连结FG和HI,则FG+HI的最小值为________.
23.(2020·重庆一中七年级期末)如图,在线段两侧作和,使,,为边上一点,满足,为直线上的动点,连接、.已知,,的周长为3.6,则的最小值为______.
24.(2020·竹溪县实验中学九年级其他模拟)如图,在菱形ABCD中,AB=,BD=6,M、N分别是BC,CD的中点,P是对角线BD上的一个动点,则△PMN周长的最小值为_____.
25.(2020·武汉市光谷实验中学九年级月考)如图,矩形ABCD中,AB=2,BC=9,点P时矩形ABCD内一动点,且=,则PC+PD的最小值是_________.
26.(2020·四川武外八年级月考)如图,正方形,边上有一点,,,在上有一点,使为最短.则最短距离为 _________.
27.(2020·常熟市第一中学八年级月考)如图,在长方形ABCD中,AB=5,AD=4,动点P满足长方形ABCD,则点P到C,D两点的距离之和PC+PD的最小值为________.
28.(2020·常州市武进区星辰实验学校八年级月考)如图,∠MON=90°,长方形ABCD的顶点B、 C分别在边OM、ON上,当B在边OM上运动时,C随之在边ON上运动.若CD=3,BC=8,运动过程中,点D到点O的最大距离为_________.
29.(2019·山西八年级期末)如图,正方形ABCD中,AB=2,AC,BD交于点O.若E,F分别是边AB,BC上的动点,且,则△OFF周长的最小值是________________;
30.(2020·山西八年级月考)如图,在菱形中,,点是边的中点,是对角线上的一个动点,连接,,若,则的最小值是__________.
31.(2020·郎溪县第二中学九年级)如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD的方向平移得到△A'B'D',分别连接A'C,A'D,B'C,则A'C+B'C的最小值为_____.
32.(2020·内蒙古包头市·包头外国语实验学校八年级期中)如图,四边形OABC为正方形,边长为10,点A,C分别在x轴、y轴的正半轴上,点D在OA上,且D点的坐标为(4,0),P是OB上的一个动点,则PD+PA的最小值是_____.
33.(2020·辽宁锦州市·九年级期中)如图,在平面直角坐标系中,点A、C分别在x轴、y轴上,四边形是边长为2的正方形,点D为的中点,点P为上的一个动点,连接、,当点P满足的值最小时,则点P的坐标为______.
34.(2020·成都市铁中府河学校九年级期中)如图,在矩形中,,垂足为,动点分别在上,则的值为__________,的最小值为_____________.
35.(2020·福建省福州第十九中学八年级期中)如图,四边形中,,,点为直线左侧平面上一点,的面积为则的最大值为___.
36.(2020·武城县实验中学八年级期中)如图,在五边形中,,,,,在,上分别找一点,,使得的周长最小时,则的度数为_______.
37.(2020·深圳亚迪学校)如图,菱形ABCD的边长为6,,对角线BD上有两个动点E、F(点E在点F的左侧),若,则的最小值为________.
38.(2020·成都西川中学九年级期中)如图,在矩形纸片中,,,点是的中点,点是上一动点.将沿直线折叠,点落在点处,在上任取一点,连接,,,则的周长的最小值为________.
39.(2020·湖北华一寄宿学校八年级月考)如图所示,长方形中,,,,点为上的任意一点(可与、 重合),分别过、、作射线的垂线,垂足分别为、、,则的最小值为___________.
40.(2020·武汉二中广雅中学九年级二模)如图,M为矩形ABCD中AD边中点,E、F分别为BC、CD上的动点,且BE=2DF,若AB=1,BC=2,则ME+2AF的最小值为________.
参考答案
1.B
【分析】
由正方形的中心对称性质,可得 的最小值即是DE的值,再由勾股定理解题计算即可.
【详解】
连接DE,交AC于点P,连接BD,
点B与点D关于AC对称,
的长即为的最小值,
是BC的中点,
,
在中,
的最小值是.
故选:B.
【点拨】
本题考查两点对称的性质、两点间的距离、勾股定理等知识,是重要考点,难度较易,掌握相关知识是解题关键.
2.D
【分析】
由正方形的性质得出B、D关于AC对称,根据两点之间线段最短可知,连接DE,交AC于P,连接BP,则此时PB+PE的值最小,进而利用勾股定理求出即可.
【详解】
解:如图,连接DE,交AC于P,连接BP,则此时PB+PE的值最小,
∵四边形ABCD是正方形,
∴B、D关于AC对称,
∴PB=PD,
∴PB+PE=PD+PE=DE.
∵BE=2,AE=4,
∴AD=AB=6,
∴DE==2,
故PB+PE的最小值是2.
故选:D.
【点拨】
本题考查轴对称—最短路线问题,其中涉及正方形的性质、勾股定理等知识,是重要考点,难度较易,掌握相关知识是解题关键
3.B
【分析】
由于点B与D关于AC对称,所以连接BE,与AC的交点即为P点.此时PD+PE=BE最小,而BE是等边△ABE的边,BE=AB,由正方形ABCD的面积为16,可求出AB的长,从而得出结果.
【详解】
解:设BE与AC交于点P',连接BD.
∵点B与D关于AC对称,
∴P'D=P'B,
∴P'D+P'E=P'B+P'E=BE最小.
∵正方形ABCD的面积为16,
∴AB=4,
又∵△ABE是等边三角形,
∴BE=AB=4.
故选:B.
【点拨】
本题考查的是正方形的性质和轴对称-最短路线问题,熟知“两点之间,线段最短”是解答此题的关键.
4.D
【分析】
连接,作点A关于BC的对称点A′,连接BA′、EA′,易得,当D、E、A′在同一直线时,最小,利用勾股定理求解即可.
【详解】
连接,根据正方形的性质及,可得△DCE≌△ADF,
则有,
,
作点A关于BC的对称点A′,连接BA′、EA′,
则AE=A ′E,
即,
当D、E、A′在同一直线时,最小,
AA′=2AB=4,
此时,在Rt△ADA′中,DA′=,
故的最小值为,
故答案为:D.
【点拨】
本题考查正方形的性质和最短距离问题,解题的关键是把两条线段的和转化在同一条线段上求解.
5.C
【分析】
由于点B与点D关于AC对称,所以连接DE,交AC于点P,此时BP+PE最小为线段DE的长,在Rt△DAE中,由勾股定理先计算出DE的长度即可.
【详解】
连接DE,与AC的交点为P,此时BP+PE最小,
∵四边形ABCD是正方形,且周长为8,
∴AC⊥BD,BO=OD,AD=AB=2,
∴点B与点D关于AC对称,
∴BP=DP,
∴BP+PE=DP+PE=DE,
∵E是AB的中点,
∴AE=AB=1,
在Rt△ADE中,DE2=AD2+AE2,
∴DE==,
故选C.
【点拨】
此题考查轴对称问题,根据两点之间线段最短,确定点P的位置是解题关键.
6.D
【分析】
如图,连接MB交AC于N,此时DN+MN最小,先证明这个最小值就是线段BM的长,利用勾股定理就是即可解决问题.
【详解】
解:如图,连接MB交AC于N,此时DN+MN最小.
∵四边形ABCD是正方形,
∴B、D关于AC对称,
∴DN=BN,
∴DN+MN=BN+NM=BM,
在RT△BMC中,∵∠BCM=90°,BC=4,CM=CD﹣DM=4﹣1=3,
∴BM===5.
故选:D.
【点拨】
本题考查了最短路径问题、正方形性质、勾股定理、两点之间线段最短等知识,解题的关键是利用对称找到点N的位置.
7.C
【分析】
要使DN+MN最小,首先应分析点N的位置.根据正方形的性质:正方形的对角线互相垂直平分.知点D的对称点是点B,连接MB交AC于点N,此时DN+MN最小值即是BM的长.
【详解】
解:根据题意,连接BD、BM,则BM就是所求DN+MN的最小值,
在Rt△BCM中,BC=16,CM=16-4=12,
根据勾股定理得:BM==20,
即DN+MN的最小值是20;
故选:C.
【点拨】
此题考查了正方形的性质,勾股定理,以及轴对称问题,此题的难点在于确定满足条件的点N的位置.
8.B
【详解】
∵四边形ABCD是菱形,∴点B与点D关于直线AC对称.
如图,连接BE与AC相交于点P,由轴对称确定最短路线问题,BE的长度即为PE+PD的最小值,连接BD.
∵∠B=120°,∴∠BCD=180°−120°=60°.
又∵BC=CD,∴△BCD是等边三角形.
∵E是CD的中点,
.
故选B.
9.B
【分析】
由于点B与D关于AC对称,所以连接BD,与AC的交点即为F点.此时PD+PE=BE最小,而BE是等边△ABE的边,BE=AB,由正方形ABCD的面积为12,可求出AB的长,即可得到PD+PE的最小值,从而可得结果.
【详解】
解:连接BD,与AC交于点F.
∵点B与D关于AC对称,
∴PD=PB,
∴PD+PE=PB+PE=BE最小.
∵正方形ABCD的面积为12,
∴AB=,
又∵△ABE是等边三角形,
∴BE=AB=,
故所求最小值为,
则图中长度等于的线段共有AB、BC、CD、AD、BE、AE共6条,
故选B.
【点拨】
此题主要考查轴对称—最短路线问题,要灵活运用对称性解决此类问题.
10.A
【分析】
作点F关于AC的对称点,根据轴对称的性质得到,即线段的长度就是的最小值,再根据正方形的性质求出的长.
【详解】
解:如图,作点F关于AC的对称点,
根据正方形的轴对称性,点在线段AD的中点处,
连接,此时最小,
∵E、分别是BC和AD的中点,
∴,,
∵四边形ABCD的正方形,
∴,,
∴,
∴四边形是平行四边形,
∴.
故选:A.
【点拨】
本题考查线段和最小问题,解题的关键是掌握正方形的性质以及利用轴对称的性质求线段和最小的方法.
11.C
【分析】
作点E关于CD的对称点H,连接AH,根据轴对称的性质及两点之间线段最短可得AF+EF的最小值为AH,进而可求△AEF周长的最小值.
【详解】
解:作点E关于CD的对称点H,连接AH,如图所示:
EC=CH,
四边形是矩形,,,
AB=CD=5,AD=BC=8,∠B=90°,
点若为的中点,
BE=EC=CH=4,
BH=12,
在Rt△ABE中,,
,
若使△AEF的周长为最小值,则需满足AF+EF为最小,
根据轴对称的性质及两点之间线段最短可知AF+EF的最小值为AH,
在Rt△ABH中,,
△AEF的周长最小值为;
故选C.
【点拨】
本题主要考查矩形的性质、轴对称的性质及勾股定理,熟练掌握矩形的性质、轴对称的性质及勾股定理是解决最短路径的关键.
12.B
【分析】
根据菱形的对角线互相垂直平分,点关于的对称点是点,连接,最小值 ,然后解直角三角形即可求解.
【详解】
解:在菱形中,与互相垂直平分,
点、关于对称,
连接,则就是所求的的最小值的线段,
为的中点,,
∴ABD是等边三角形,
,
,
的最小值为.
故选:B.
【点拨】
本题主要考查了菱形的性质以及利用轴对称性求两条线段和的最小值,关键是通过轴对称找出点F的位置,使最小.
13.C
【分析】
利用菱形的性质及相切两圆的性质得出P与D重合时的最小值,进而求解即可.
【详解】
解:作点A关于直线CD的对称点A´,连接BD,DA´,
∵四边形ABCD是菱形,
∴AB=AD,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴∠ADB=60°,
∵∠BDC=∠ADB=60°,
∴∠ADN =60°,
∴∠A´DN=60°,
∴∠ADB+∠ADA´=180°,
∴A´,D,B在一条直线上,
由此可得:当点P和点D重合,E点在AD上,F点在BD上,此时最小,
∵在菱形ABCD中,∠A=60°,
∴AB=AD,
则△ABD为等边三角形,
∴BD=AB=AD=3,
∵⊙A,⊙B的半径分别为2和1,
∴PE=1,DF=2,
∴的最小值为3.
故选C.
【点拨】
本题考查了菱形的性质,等边三角形的性质,点与圆的位置关系等知识.根据题意得出点P位置是解题的关键.
14.A
【分析】
先根据轴对称性质和两点间线段最短,确定MD是PM+PB的最小值的情况,在Rt△AMD中根据含30度角的直角三角形的性质及勾股定理即可求出AD的值,最后根据菱形的性质即可得出答案.
【详解】
连接PD,BD,
∵PB=PD,
∴PM+PB=PM+PD,
连接MD,交AC的点就是P点,根据两点间直线最短,
∴这个P点就是要的P点,
又∵∠BAD=60°,AB=AD,
∴△ABD是等边三角形,∠ADM=30°
∵M为AB的中点,
∴MD⊥AB,
∵MD=9,
∴AD2= +
解得: AD=
∴AB=.
故选:A.
【点拨】
本题考查的是菱形的性质、勾股定理、含30度角的直角三角形,解题的关键是熟练掌握所学知识,属中等难度.
15.A
【分析】
作点E关于DC的对称点E,设AB的中点为点O,连接OE,交DC于点P,连接PE,由轴对称的性质及90°的圆周角所对的弦是直径,可知线段PE+PM的最小值为OE的值减去以AB为直径的圆的半径OM,根据正方形的性质及勾股定理计算即可.
【详解】
解答:解:作点E关于DC的对称点E,设AB的中点为点O,连接OE,交DC于点P,连接PE,如图:
∵动点M在边长为2的正方形ABCD内,且AM⊥BM,
∴点M在以AB为直径的圆上,OM=AB=1,
∵正方形ABCD的边长为2,
∴AD=AB=2,∠DAB=90°,
∵E是AD的中点,
∴DE=AD=×2=1,
∵点E与点E关于DC对称,
∴DE=DE=1,PE=PE,
∴AE=AD+DE=2+1=3,
在Rt△AOE中,OE===,
∴线段PE+PM的最小值为:
PE+PM
=PE+PM
=ME
=OE−OM
=−1.
故选:A.
【点拨】
本题考查了轴对称−最短路线问题、圆周角定理的推论、正方形的性质及勾股定理等知识点,数形结合并熟练掌握相关性质及定理是解题的关键.
16.C
【分析】
作点B关于对角线AC的对称点,该对称点与D重合,连接DM,则PB与PM之和的最小值为DM的长;由菱形的面积可求出BD=4,由题意可证△BCD是等边三角形,由等边三角形的性质可得DM⊥BC,CM=BM=2,由勾股定理可求DM=2.
【详解】
解:作点B关于对角线AC的对称点,该对称点与D重合,连接DM,则PB与PM之和的最小值为DM的长;
∵菱形ABCD的面积为8,对角线AC长为4,
∴BD=4,
∵BC=CD,∠BCD=60°,
∴△BCD是等边三角形,
∴BD=BC=4,
∵M是BC的中点,
∴DM⊥BC,CM=BM=2,
在Rt△CDM中,CM=2,CD=4,
∴DM=,
故选:C.
【点拨】
本题考查了轴对称-最短路线问题,菱形的性质,等边三角形的性质,直角三角形勾股定理;掌握利用轴对称求最短距离,将PB与PM之和的最小值转化为线段DM的长是解题的关键.
17.B
【分析】
首先由,得知动点P在与AB平行且与AB的距离为3的直线上,作点A关于直线的对称点E,连接AE、BE,则BE的长就是所求的最短距离,然后在直角三角形ABE中,由勾股定理求得BE的值,即PA+PB的最小值.
【详解】
解:∵, 设点P到CD的距离为h,则点P到AB的距离为(4-h),
则,解得:h=1,∴点P到CD的距离1,到AB的距离为3,
∴如下图所示,动点P在与AB平行且与AB的距离为3的直线上,作点A关于直线的对称点E,连接AE、BE,且两点之间线段最短,
∴PA+PB的最小值即为BE的长度,AE=6,AB=3,∠BAE=90°,
根据勾股定理:,
故选:B.
【点拨】
本题考查了轴对称—最短路线问题(两点之间线段最短),勾股定理,得出动点P所在的位置是解题的关键.
18.A
【分析】
根据题意作出D关于OB的对称点D′,则D′的坐标是(0,2).则PD+PA的最小值就是AD′的长,利用勾股定理进行计算即可求解.
【详解】
解:作出D关于OB的对称点D′,
则D′的坐标是(0,2).则PD+PA的最小值就是AD′的长.
则OD′=2,
因而AD′=.
则PD+PA和的最小值是2.
故选:A.
【点拨】
本题考查正方形的性质以及最短路线问题,根据题意正确作出P的位置以及运用勾股定理进行计算是解题的关键.
19.A
【分析】
将△BPC绕点C逆时针旋转60°,得到△EFC,连接PF、AE、AC,则AE的长即为所求.
【详解】
解:如图,将△BPC绕点C逆时针旋转60°,得到△EFC,连接PF、 AE 、AC,则AE的长即为所求.
由旋转的性质可知:△PFC是等边三角形,∴PC=PF,
∵PB=EF,∴PA+PB+PC=PA+PF+EF,
∴当A、P、F、 E 共线时,PA+PB+PC的值最小,
∵四边形ABCD是矩形,∴∠ABC=90°,
∴tan∠ACB=,∴∠ACB=30°,AC=2AB= ,
∵∠BCE=60°,∴∠ACE=90°,
∴AE=.
故选A.
【点拨】
本题考查轴对称−最短问题、矩形的性质、旋转变换等知识,解题的关键是学会添加常用辅助线,学会用转化的思想思考问题,属于中考常考题型.
20.A
【分析】
①根据正方形的对角线平分对角的性质,得是等腰直角三角形,在中,,求得;
②根据等腰直角三角形和矩形的性质可得其周长为2BC,则四边形PECF的周长为8;
③根据P的任意性可以判断不一定是等腰三角形;
④由PECF为矩形,则通过正方形的轴对称性,证明;
⑤当AP最小时,EF最小,EF的最小值等于.
【详解】
①如图,延长FP交AB与G,连PC,延长AP交EF与H,
∵PE⊥BC,PF⊥CD,∠BCD=90°,
∴四边形PECF为矩形,
∴PF=CE,
∵GF∥BC,
∴∠DPF=∠DBC,
∵四边形ABCD是正方形,
∴∠DBC=45°
∴∠DPF=∠DBC=45°,
∴∠PDF=∠DPF=45°,
∴PF=EC=DF,
∴在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,
∴DP=EC.
故①正确;
②∵四边形PECF为矩形,
∴四边形PECF的周长=2CE+2PE=2CE+2BE=2BC=8,
故②正确;
③∵点P是正方形ABCD的对角线BD上任意一点,∠ADP=45,
∴当∠PAD=45或67.5或90时,△APD是等腰三角形,
除此之外,△APD不是等腰三角形,
故③错误;
④∵四边形PECF为矩形,
∴PC=EF,
由正方形为轴对称图形,
∴AP=PC,
∴AP=EF,
故④正确;
⑤BD=,
由EF=PC,
∴当PC最小时,EF最小,
则当PC⊥BD时,即PC=BD=时,EF的最小值等于,
故⑤正确;
综上所述,①②④⑤正确,
故选:A.
【点拨】
本题考查了正方形的性质,等腰三角形的判定和性质,勾股定理的应用.本题难度较大,综合性较强,在解答时要认真审题.
21.32
【分析】
连接交直线于点,则此时,可知的周长最小,求出,,则可得出答案.
【详解】
解:将矩形沿直线折叠,使直线两侧的部分能够完全重合,
点与点关于直线对称,
连接交直线于点,则此时,,
的周长最小.
,,
,,
矩形中,,,,
,
的周长.
即周长的最小值是32.
故答案为:32.
【点拨】
本题考查了矩形的性质,折叠的性质,勾股定理,轴对称的性质等知识,熟练掌握几何图形的性质是解题的关键.
22.3
【分析】
先证明得到再证明:四边形 四边形为矩形,得到,所以只要求的最小值即可,当时,最小,再利用锐角三角函数可得答案.
【详解】
解: AB=BC=3,∠A=∠C=90°,
由过点E分别作AB,BC,CD,AD的垂线,垂足分别为点F,H,I,G,
四边形 四边形为矩形,
当最小,则最小,
四边形为矩形,
所以:当时,最小,
所以:的最小值是:
所以:的最小值是:
故答案为:
【点拨】
本题考查的是点到直线的距离垂线段最短,三角形全等的判定与性质,矩形的判定与性质,锐角三角函数的应用,掌握以上知识是解题的关键.
23.2.8
【分析】
在BC上取CD′=BD,连接AD′,证明△ACD′≌△ABD,得到AD′=AD,∠CAD′=∠BAD,从而证明△AED′≌△AED,得到D′E=DE,∠AED′=∠AED,过A作AF⊥BC,AF与BC交于点F,从而推断出BP+DP=BP+D′P最小值为P点与E点重合时,BP与D′P共线,BP+D′P=BD′,利用勾股定理求出BD′的长度即可.
【详解】
解:在BC上取CD′=BD,连接AD′,
∵AC=AB,
∴∠C=∠ABC,
∵∠ABC=∠ABD,
∴∠C=∠ABD,又CD′=BD,AC=AB,
∴△ACD′≌△ABD(SAS),
∴AD′=AD,∠CAD′=∠BAD,
∴∠DAD′=∠BAC,
∵2∠EAD=∠BAC=∠DAD′,
∴∠D′AE=∠DAE,
又AD′=AD,AE=AE,
∴△AED′≌△AED(SAS),
∴D′E=DE,∠AED′=∠AED,
∴D′在直线BD上,
过A作AF⊥BC,AF与BC交于点F,
∵CD′=BD,D′E=DE,
∴CD′+D′E+EB=BC=BD+DE+BE=3.6,
∵P为AE上的动点,故BP+DP=BP+D′P最小值为P点与E点重合时,BP与D′P共线,BP+D′P=BD′,
∵△ABC中,AB=AC=3,BC=3.6,AF⊥BC,AD′=AD=2.6,
∴F为BC中点,即CF=BF=BC=×3.6=1.8,
∴AF=,
∴D′F=,
∴BD′=BF+D′F=1.8+1=2.8,
∴BP+DP的最小值为2.8,
故答案为:2.8.
【点拨】
本题考查了最短路径问题,全等三角形的判定和性质,勾股定理,解题的关键正确作出辅助线,利用全等三角形的性质得到相等线段.
24..
【分析】
作M关于BD的对称点E,连接NE,交BD于P,连接MP,此时MP+NP的值最小.此时△PMN的周长最小.
【详解】
解:如图,作ME⊥BD交AB于E,连接EN,与BD交于点P',
当P与P'重合时,则EN就是PM+PN的最小值,
∵M、N分别是BC、CD的中点,
∴CN=BM=CM,
∵ME⊥BD交AB于E,
∴BE=BM,
∴BE=CN,BE∥CN,
∴四边形BCNE是平行四边形,
∴,
∴DN=NC,CM=BM,
∴,
∴△PMN的周长的最小值为.
故选答案为.
【点拨】
此题考查菱形的性质和轴对称及平行四边形的判定等知识的综合应用.综合运用这些知识是解决本题的关键.
25.2
【分析】
如图,作PM⊥AD于M,作点D关于直线PM的对称点E,连接PE,EC.设AM=x.由PM垂直平分线段DE,推出PD=PE,推出PC+PD=PC+PE≥EC,利用勾股定理求出EC的值即可.
【详解】
解:如图,作PM⊥AD于M,作点D关于直线PM的对称点E,连接PE,EC.设AM=x.
∵四边形ABC都是矩形,
∴ABCD,AB=CD=2,BC=AD=9,
∵=,
∴×2×x=××2×(9-x),
∴x=3,
∴AM=3,DM=EM=6,
在RtECD中,EC==2,
∵PM垂直平分线段DE,
∴PD=PE,
∴PC+PD=PC+PE≥EC,
∴PD+PC≥2,
∴PD+PC的最小值为2.
【点拨】
本题考查轴对称-最短问题,三角形的面积,矩形的性质等知识,解题的关键是学会添加常用辅助线,学会用转化的思想思考问题,属于中考常考题型.
26.
【分析】
连接DE,交直线AC于点P,根据四边形ABCD是正方形可知B、D关于直线AC对称,所以DE的长即为EP+BP的最短距离,再根据勾股定理即可得出结论.
【详解】
连接DE,交直线AC于点P,
∵四边形ABCD是正方形,
∴B、D关于直线AC对称,
∴DE的长即为EP+BP的最短距离,
∵AE=3,EB=1,
∴AD=AB=AE+BE=4,
∴DE=.
故答案为:.
【点拨】
本题考查了轴对称-最短路线问题、正方形的性质以及勾股定理的运用,熟知两点之间线段最短是解答此题的关键.
27.
【分析】
首先证明动点P在与CD平行且与CD的距离是2的直线l上,由A,D关于直线l对称,连接AC,则AC的长就是所求的最短距离.
【详解】
设△PAB中AB边上的高是h.
∵S△PAB=S矩形ABCD,
∴•AB•h=•AB•AD,
∴h=AD=2,
∴动点P在与CD平行且与CD的距离是2的直线l上,
∵A,D关于直线l对称,连接AC交直线l于点P,则AC的长就是所求的最短距离.
∵四边形ABCD是矩形,
∴BC=AD=4,
在Rt△ABC中,∵AB=5,BC=4,
∴AC=,
即PA+PB的最小值为,
故填:.
【点拨】
本题考查了轴对称−最短路线问题,三角形的面积,矩形的性质,勾股定理,两点之间线段最短的性质.得出动点P所在的位置是解题的关键.
28.
【分析】
如图,取BC的中点E,连接OE、DE、OD,由可得当当O、D、E三点共线时,点D到点O的距离最大,进而根据直角三角形斜边中线定理及勾股定理可求解.
【详解】
解:
如图,取BC的中点E,连接OE、DE、OD,
∵,
∴当O、D、E三点共线时,点D到点O的距离最大,
此时,∵CD=3,BC=8,∠DCB=90°,
∴OE=EC=BC=4,
DE=,
∴OD的最大值为:4+5=9.
故答案为9.
【点拨】
本题主要考查直角三角形斜边中线定理及勾股定理,熟练掌握直角三角形斜边中线定理及勾股定理是解题的关键.
29.2+
【分析】
根据正方形的对角线互相平分且相等可得AO=BO,∠AOB=90°,对角线平分一组对角可得∠OAE=∠OBF,再根据AE=BF,然后利用“SAS”证明△AOE和△BOF全等,根据全等三角形对应角相等可得∠AOE=∠BOF,可得∠EOF=90°,然后利用勾股定理列式计算即可得解.
【详解】
解:在正方形ABCD中,AO=BO,∠AOB=90°,∠OAE=∠OBF=45°,
∵点E、F的速度相等,
∴AE=BF,
在△AOE和△BOF中,
,
∴△AOE≌△BOF(SAS),
∴∠AOE=∠BOF,
∴∠AOE+∠BOE=90°,
∴∠BOF+∠BOE=90°,
∴∠EOF=90°,
在Rt△BEF中,设AE=x,则BF=x,BE=2-x,
∴EF===,
∴当x=1时,EF有最小值为.
由勾股定理得,OE=OF==1.
∴△OEF周长的最小值=2+.
故答案为:2+.
【点拨】
本题考查了正方形的性质,全等三角形的判定与性质,同角的余角相等的性质,以及勾股定理等知识,熟记正方形的性质,找出三角形全等的条件是解题的关键.
30.
【分析】
找出B点关于AC的对称点D,连接DE交AC于P,则DE就是PB+PE的最小值,求出即可.
【详解】
连接DE交AC于P,连接DE,DB,
由菱形的对角线互相垂直平分,可得B、D关于AC对称,则PD=PB,
∴PE+PB=PE+PD=DE,
即DE就是PE+PB的最小值,
∵∠BAD=60°,AD=AB,
∴△ABD是等边三角形,
∴ AD=AB=2,
∵点E是AB的中点,
∴AE=BE=1,
∴DE⊥AB(等腰三角形三线合一的性质).
在Rt△ADE中,DE==.
即PB+PE的最小值为,
故填:.
【点拨】
本题主要考查轴对称−最短路线问题,菱形的性质,勾股定理等知识点,确定P点的位置是解答本题的关键.
31.
【分析】
根据菱形的性质得到AB=1,∠ABD=30°,根据平移的性质得到A′B′=AB=1,A′B′∥AB,推出四边形A′B′CD是平行四边形,得到A′D=B′C,于是得到A'C+B'C的最小值=A′C+A′D的最小值,根据平移的性质得到点A′在过点A且平行于BD的定直线上,作点D关于定直线的对称点E,连接CE交定直线于A′,则CE的长度即为A'C+B'C的最小值,求得DE=CD,得到∠E=∠DCE=30°,于是得到结论.
【详解】
解:∵在边长为1的菱形ABCD中,∠ABC=60°,
∴AB=CD=1,∠ABD=30°,
∵将△ABD沿射线BD的方向平移得到△A'B'D',
∴A′B′=AB=1,A′B′∥AB,
∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,
∴∠BAD=120°,
∴A′B′=CD,A′B′∥CD,
∴四边形A′B′CD是平行四边形,
∴A′D=B′C,
∴A'C+B'C的最小值=A′C+A′D的最小值,
∵点A′在过点A且平行于BD的定直线上,
∴作点D关于定直线的对称点E,连接CE交定直线于A′,
则CE的长度即为A'C+B'C的最小值,
∵∠A′AD=∠ADB=30°,AD=1,
∴∠ADE=60°,DH=EH=AD=,
∴DE=1,
∴DE=CD,
∵∠CDE=∠EDB′+∠CDB=90°+30°=120°,
∴∠E=∠DCE=30°,
∴CE=2×CD=.
故答案为:.
【点拨】
本题考查了轴对称-最短路线问题,菱形的性质,矩形的判定和性质,解直角三角形,平移的性质,正确地理解题意是解题的关键.
32..
【分析】
作出D关于OB的对称点D′,则D′的坐标是(0,4).则PD+PA的最小值就是AD′的长,利用勾股定理即可求解.
【详解】
解:作出D关于OB的对称点D′,则D′的坐标是(0,4).则PD+PA的最小值就是AD′的长.
则OD′=4,OA=10,
∴AD′=
则PD+PA和的最小值是.
故答案是:.
【点拨】
本题考查了正方形的性质,勾股定理以及最短路线问题,正确作出P的位置是关键.
33.
【分析】
根据正方形的性质得到点A,C关于直线OB对称,连接CD交OB于P,连接PA,PD,则此时,PD+AP的值最小,求得直线CD的解析式为y=-x+2,由于直线OB的解析式为y=x,解方程组得到P(,)即可.
【详解】
解:∵四边形ABCO是正方形,
∴点A,C关于直线OB对称,
连接CD交OB于P,连接PA,PD,则此时,PD+AP的值最小,
∵OC=OA=AB=2,
∴C(0,2),A(2,0),
∵D为AB的中点,
∴AD=AB=1,
∴D(2,1),
设直线CD的解析式为:y=kx+b,
∴,
∴,
∴直线CD的解析式为:y=-x+2,
∵直线OB的解析式为y=x,
∴,
解得:x=y=,
∴P(,),
故答案为:(,).
【点拨】
本题考查了正方形的性质,轴对称-最短路线问题,待定系数法求一次函数的解析式,正确求出直线CD的解析式是解题的关键.
34.3
【分析】
在Rt△ABE中,利用三角形相似可求得AE、DE的长,设A点关于BD的对称点A′,连接A′D,可证明△ADA′为等边三角形,当PQ⊥AD时,则PQ最小,所以当A′Q⊥AD时AP+PQ最小,从而可求得AP+PQ的最小值等于DE的长.
【详解】
设,则,
∵四边形为矩形,且,
,,
,
又,
,
,即,
,
在中,由勾股定理可得,
即,解得:,
,
如图,设点关于的对称点为,连接,
则,
是等边三角形,
,
∴当、三点在一条线上时,最小,
由垂线段最短可知当时,最小,
.
故答案是:3;.
【点拨】
本题主要考查轴对称的应用,利用最小值的常规解法确定出A的对称点,从而确定出AP+PQ的最小值的位置是解题的关键,利用条件证明△A′DA是等边三角形,借助几何图形的性质可以减少复杂的计算.
35.10
【分析】
如图,过点F作FH⊥EC于H.过点F作直线l//EC,作点C关于直线l的对称点C',连接AC'交直线l于F',此时|F'A−F'C'|的值最大,即|FA−FC|的值最大,最大值为线段AC'的长.
【详解】
解:如图,过点F作 FH⊥EC 于H.
∵△CFE的面积为8,即EC⋅FH=8,CE=8,
∴FH=2,
过点F作直线l//EC,作点C关于直线l的对称点C',连接AC'交直线l于F',此时|F'A−F'C'|的值最大,即|FA−FC|的值最大,最大值为线段AC'的长,过点C'作C'K⊥AB于K.∵∠C'KB=∠KEC=∠ECC'=90° ,
∴四边形CEKC'是矩形,
∴CC'=EK=4,EC=KC'=8,
∵AE=10,
∴AK=AE−EK=10−4=6,
∴AC'=,
∴|FA−FC|的最大值为10.
故答案为10.
【点拨】
本题考查轴对称−最短问题,三角形的面积,直角梯形等知识,解题的关键是学会利用轴对称解决最值问题,属于中考填空题中的压轴题.
36.
【分析】
如图(见解析),先根据轴对称的性质可得,再根据三角形的周长公式、两点之间线段最短可得当点在同一条直线上时,的周长最小,然后利用等腰三角形的性质、三角形的外角性质即可得.
【详解】
如图,作点A关于BC的对称点,关于DE的对称点,连接、,
则,
的周长为,
由两点之间线段最短可知,当点在同一条直线上时,的周长最小,
,
,
,
,
,
,
,
,
故答案为:.
【点拨】
本题考查了轴对称的性质、等腰三角形的性质、两点之间线段最短等知识点,正确找出的周长最小时,点M、N的位置是解题关键.
37.
【分析】
作AM⊥AC,连接CM交BD于F,根据菱形的性质和等边三角形的判定和性质以及勾股定理解答即可.
【详解】
如图,连接AC,作AM⊥AC,使得AM=EF=2,连接CM交BD于F,
∵AC,BD是菱形ABCD的对角线,
∴BD⊥AC,
∵AM⊥AC,
∴AM∥BD,
∴AM∥EF,
∵AM=EF,AM∥EF,
∴四边形AEFM是平行四边形,
∴AE=FM,
∴AE+CF=FM+FC=CM,
根据两点之间线段最短可知,此时AE+FC最短,
∵四边形ABCD是菱形,AB=6,∠ABC=60°
∴BC=AB,
∴△ABC是等边三角形,
∴AC=AB=6,
在Rt△CAM中,CM=
∴AE+CF的最小值为.
故答案为:.
【点拨】
本题考查菱形的性质、平行四边形的判定和性质、两点之间线段最短、勾股定理等知识,解题的关键是学会添加常用辅助线,把问题转化为两点之间线段最短解决,属于中考填空题中的压轴题.
38.
【分析】
如图,当点F固定时,连接AC交EF于G,连接,此时△ 的周长最小,最小值=,当最小时,△的周长最小,求出的最小值即可解决问题;
【详解】
如图所示,当点F固定时,连接AC交EF于G,连接,
此时△ 的周长最小,
最小值=,
∵ 四边形ABCD 矩形,
∴∠D=90°,AD=BC=3,CD=AB=4,
∴AC===5,
所以△的周长的最小值=5+,
当最小时,△的周长最小,
∵AE=DE==,
∴CE==,
∵≥EC-,
∴≥-,
∴ △的周长的最小值为5+-= ,
故答案为:.
【点拨】
本题考查翻折变换,矩形的性质,轴对称最短问题等知识,解题的关键是学会用转化的思想思考问题,属于中考填空题中的压轴题题型.
39.
【分析】
如图,过点B作,并交于点M,根据平行线性质,得四边形为矩形,从而得到;再根据矩形性质,通过证明,得;再根据三角形边角关系性质,得当点P和点C重合时,取最小值;通过三角形面积计算公式,计算得,从而完成求解
【详解】
如图,过点B作,并交于点M
根据题意得:,
∴,,
∴四边形为矩形,
∴
∴
∵长方形
∴,,
∴
∴
∵
∴
∴
∴
∵
∴当点P和点C重合时,取最小值,即取最小值
∴
∴
∴,即最小值为
故答案为:.
【点拨】
本题考查了矩形、平行线、垂线、全等三角形、三角形的知识;解题的关键是熟练掌握矩形、平行线、全等三角形、三角形的性质,从而完成求解.
40.
【分析】
如图,过点作于.设,则.由勾股定理得到,欲求的最小值,相当于在轴上找一点,使得点到,和的距离之和最小(如下图),作点关于轴的对称点,连接交轴于,连接,此时的值最小,最小值.
【详解】
解:如图,过点作于.设,则.
四边形是矩形,
,
,
,
四边形是矩形,
,,
,
,
欲求的最小值,相当于在轴上找一点,使得点到,和的距离之和最小(如下图),
作点关于轴的对称点,连接交轴于,连接,此时的值最小,最小值,
,,
,
的最小值为,
故答案为.
【点拨】本题考查矩形的性质,勾股定理,轴对称最短问题等知识,解题的关键是学会利用数形结合的思想解决问题.
专题33 将军饮马模型-中考数学几何模型(重点专练): 这是一份专题33 将军饮马模型-中考数学几何模型(重点专练),文件包含专题33将军饮马模型教师版-中考数学几何模型重点专练docx、专题33将军饮马模型学生版-中考数学几何模型重点专练docx等2份试卷配套教学资源,其中试卷共58页, 欢迎下载使用。
最新中考几何专项复习专题15 几何最值之将军饮马知识精讲: 这是一份最新中考几何专项复习专题15 几何最值之将军饮马知识精讲,共7页。
最新中考几何专项复习专题15 几何最值之将军饮马巩固练习(提优): 这是一份最新中考几何专项复习专题15 几何最值之将军饮马巩固练习(提优),文件包含中考几何专项复习专题15几何最值之将军饮马巩固练习提优教师版含解析docx、中考几何专项复习专题15几何最值之将军饮马巩固练习提优学生版docx等2份试卷配套教学资源,其中试卷共16页, 欢迎下载使用。













