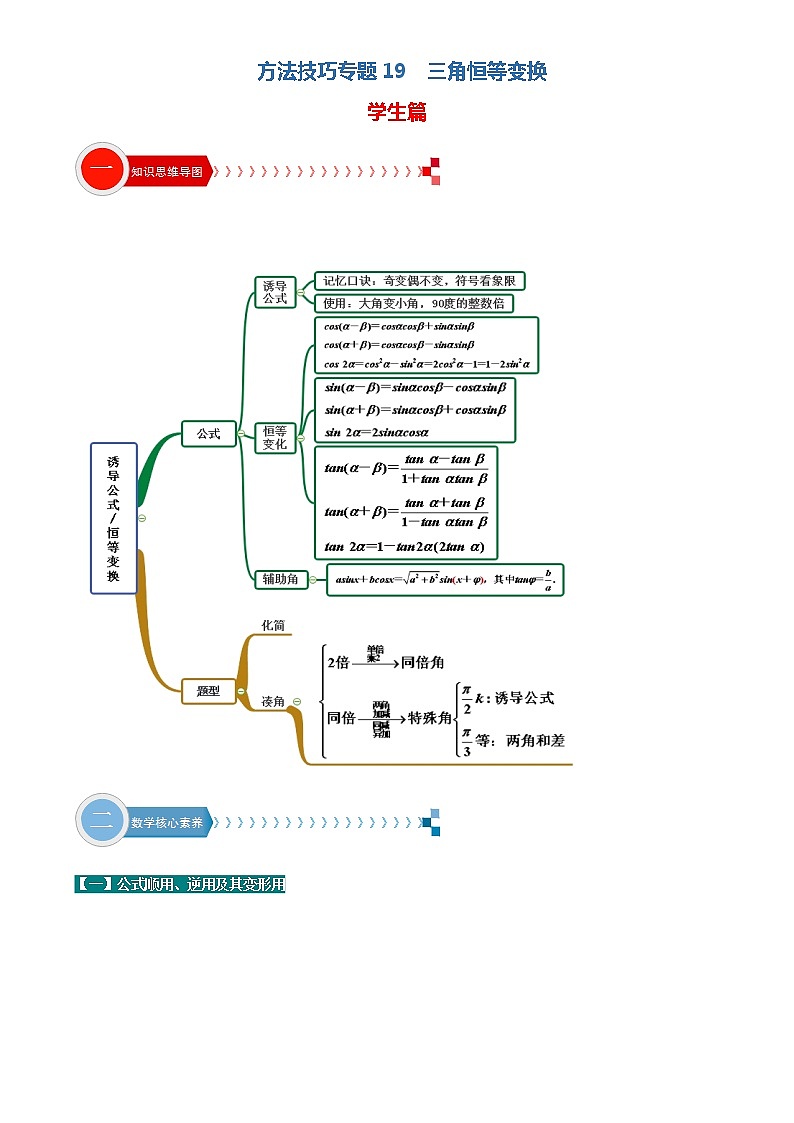
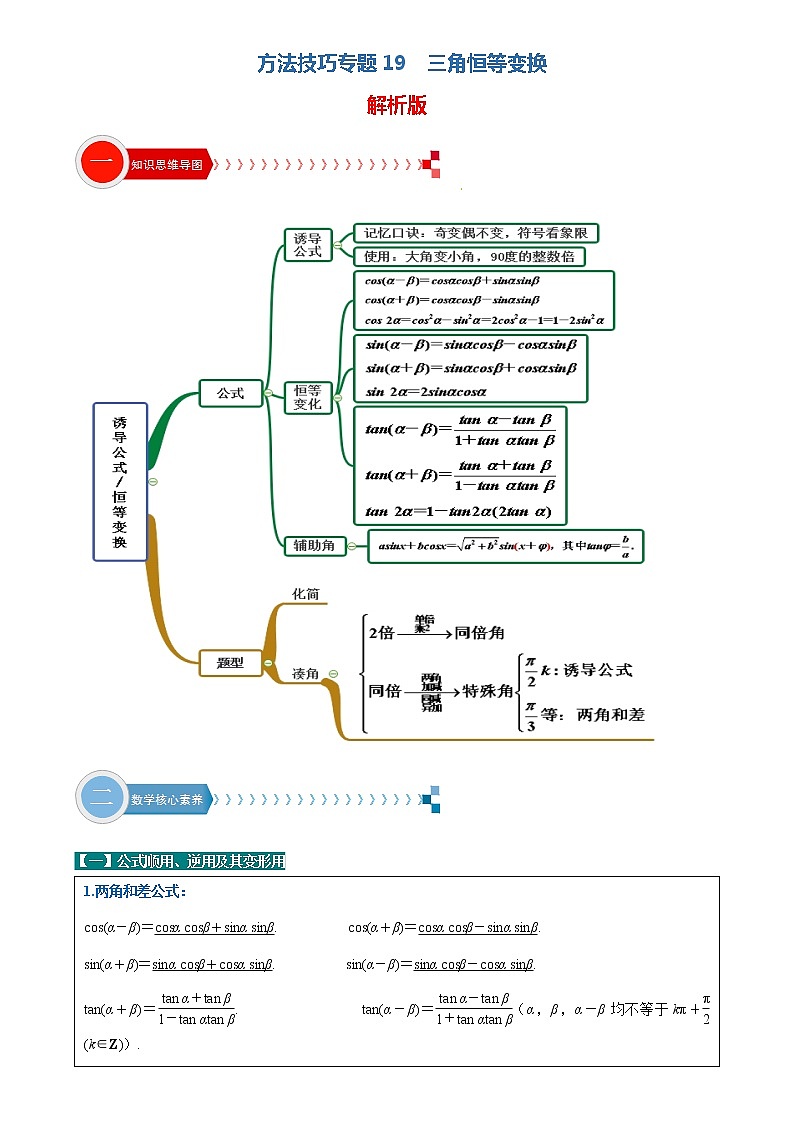
方法技巧专题19 三角恒等变换-2022年高考数学满分之路方法技巧篇

这是一份方法技巧专题19 三角恒等变换-2022年高考数学满分之路方法技巧篇，文件包含方法技巧专题19三角恒等变换解析版docx、方法技巧专题19三角恒等变换原卷版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。
 方法技巧专题19  三角恒等变换解析版             一、三角恒等变换问题知      恒等变换方法技巧                  【一】公式顺用、逆用及其变形用   1.例题【例1】计算：(1)cos(－15°)；                          (2)cos 15°cos 105°＋sin 15°sin 105°.【解析】(1)方法一　原式＝cos(30°－45°)＝cos 30°cos 45°＋sin 30°sin 45°＝×＋×＝.方法二　原式＝cos 15°＝cos(45°－30°)＝cos 45°cos 30°＋sin 45°sin 30°＝×＋×＝.(2)原式＝cos(15°－105°)＝cos(－90°)＝cos 90°＝0.【例2】(1)计算：cos2－sin2；【解析】原式＝cos ＝.(2)计算：；【解析】　＝2·＝2·＝－2.[来源:学科网ZXXK](3)计算：cos 20°cos 40°cos 80°.【解析】原式＝·2sin 20°cos 20°cos 40°cos 80°＝·sin 40°·cos 40°cos 80°＝sin 80°cos 80°＝·sin 160°＝＝. 【例3】(1)＝________.【解析】      原式＝＝tan(45°＋15°)＝tan 60°＝.(2)化简：tan 23°＋tan 37°＋tan 23°tan 37°.【解析】方法一　tan 23°＋tan 37°＋tan 23°tan 37°＝tan(23°＋37°)(1－tan 23°tan 37°)＋tan 23°tan 37°＝tan 60°(1－tan 23°tan 37°)＋tan 23°tan 37°＝.方法二　∵tan(23°＋37°)＝，∴＝，∴－tan 23°tan 37°＝tan 23°＋tan 37°，∴tan 23°＋tan 37°＋tan 23°tan 37°＝.（3）已知sin θ＝，＜θ＜3π，求cos和tan .【解析】　∵sin θ＝，且＜θ＜3π，∴cos θ＝－＝－.由cos θ＝2cos2－1，得cos2＝＝.∵＜＜，∴cos ＝－ ＝－.tan ＝＝2. 2.巩固提升综合练习 【练习1】化简cos 15°cos 45°＋cos 75°sin 45°的值为(　　)A.     B.    C．－    D．－【解析】B  cos 15°cos 45°＋cos 75°sin 45°＝cos 15°cos 45°＋sin 15°sin 45°＝cos(15°－45°)＝cos(－30°)＝. 【练习2】＝________.【解析】－1原式＝＝＝tan(30°－75°)＝－tan 45°＝－1.【练习3】在△ABC中，A＋B≠，且tan A＋tan B＋＝tan Atan B，则角C的值为(　　)A.      B.     C.     D.【解析】A∵tan A＋tan B＋＝tan Atan B⇔tan(A＋B)·(1－tan Atan B)＝(tan Atan B－1)．(*)若1－tan Atan B＝0，则cos Acos B－sin Asin B＝0，即cos(A＋B)＝0.∵0<A＋B<π，∴A＋B＝与题设矛盾．∴由(*)得tan(A＋B)＝－，即tan C＝.又∵0<C<π，∴C＝.【练习4】若sin α＋cos α＝，则sin 2α=        .【解析】由题意，得(sin α＋cos α)2＝，∴1＋2sin αcos α＝，即1＋sin 2α＝，∴sin 2α＝－.【二】拆凑角问题 1.例题【例1】已知，则 的值为(　　)A．－     B.    C.    D．－【答案】A【解析】∵sin＝，∴cos＝cos＝－sin＝－.【例2】已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，它的终边过点. 若角β满足sin(α＋β)＝，则cos β的值为________．【答案】　－或 【解析】　由角α的终边过点，得sin α＝－，cos α＝－.由sin(α＋β)＝，得cos(α＋β)＝±.由β＝(α＋β)－α，得cos β＝cos(α＋β)cos α＋sin(α＋β)sin α，所以cos β＝－或cos β＝.【例3】若，则（   ）A． B． C． D． 【答案】D【解析】 2.巩固提升综合练习【练习1】已知，则________.【答案】－【解析】tan＝tan＝tan＝－tan＝－.【练习2】若，A∈，则sin A的值为(　　)A.   B.C.或   D.【答案】B【解析】∵A∈，∴A＋∈，∴cos（A＋）＝－ ＝－，∴sin A＝sin[（A＋）- ]＝sin（A＋）cos－cos（A＋）sin＝.【练习3】已知，则（    ）A. B. C. D.【答案】C【解析】因为，则．故应选C．【练习4】若sin（）=，则cos（）=（　　）A． B． C． D．【答案】C【解析】令，则，所以，故选C．【练习5】已知，则的值为（   ）A． B． C． D．【答案】C【解析】由题意得：本题正确选项：  【三】常值代换 1.例题【例1】已知，．（1）求的值；（2）求的值．【解析】（1）∵，，∴，∴．（2）∵，∴，∴，，．  【例2】已知△ABC中,,则tanA=      .【解析】解法一：列出方程组由第一个方程得,,代入第二个方程得，即， 解得或，因为△ABC中0<A<π,所以sinA>0,，，所以. 答案:.解法二：由已知得sinA>0, cosA<0, |sin A|<|cos A|, tanA>-1,
由两边平方,整理得，即，分子分母同除以得， 解得. 2.巩固提升综合练习【练习1】已知，，则（  ）A．或 B． C． D．【答案】B【解析】因为，所以，所以，所以，即，解得或者，当时，，当时，，综上所述，，故选B。【练习2】已知，则的值为（   ）A． B． C． D．【答案】A【解析】 则 故选A.【四】辅助角公式1.例题【例1】函数f(x)＝sin x－cos x，x∈的最小值为________．【解析】　－1f(x)＝sin，x∈.∵－≤x－≤，∴f(x)min＝sin＝－1.【例2】已知函数f(x)＝sin＋2sin2 (x∈R)．(1)求函数f(x)的最小正周期；(2)求使函数f(x)取得最大值的x的集合．【解析】(1)∵f(x)＝sin＋2sin2＝sin[2]＋1－cos＝2＋1＝2sin＋1＝2sin＋1，∴f(x)的最小正周期为T＝＝π.(2)当f(x)取得最大值时，sin＝1，有2x－＝2kπ＋(k∈Z)，即x＝kπ＋ (k∈Z)，∴所求x的集合为.2.巩固提升综合练习【练习1】当函数取得最大值时，的值是______【解析】，，这时，即，所以[来源:Zxxk.Com]【练习2】如果是奇函数，则=                   .【解析】，其中，∵为奇函数，所以，即，所以  [来源:学.科.网Z.X.X.K]【练习3】已知函数f(x)＝cos·cos，g(x)＝sin 2x－.(1)求函数f(x)的最小正周期；(2)求函数h(x)＝f(x)－g(x)的最大值，并求使h(x)取得最大值时x的集合．【解析】(1)f(x)＝·＝cos2x－sin2x＝－＝cos 2x－，∴f(x)的最小正周期为T＝＝π.(2)h(x)＝f(x)－g(x)＝cos 2x－sin 2x＝cos，当2x＋＝2kπ(k∈Z)，即x＝kπ－(k∈Z)时，h(x)有最大值.此时x的集合为.                                三、课后自我检测                         [来源:Zxxk.Com]1．已知sin α＝，且α∈，则sin的值为________．【答案】－【解析】因为sin α＝，且α∈，所以α∈，所以cos α＝－＝－ ＝－.因为sin 2α＝2sin αcos α＝－，cos 2α＝2cos2α－1＝－.所以sin＝sin 2αcos＋cos 2αsin＝－.[来源:学科网ZXXK]2．若，则          。【答案】【解析】因为，又，所以，故选B.3．已知，则          。【答案】【解析】=又,解又，,故故所以故选：A4．已知，，则    。【答案】【解析】因为，诱导公式可得， ，又因为所以 5．已知sin（），则sin2x的值为（   ）【答案】【解析】设,则，6．已知，则               。 【答案】∵，∴，．7．若，，，，则等于           。【答案】【解析】，，则，，则，所以，，因此，，8．已知，为锐角，且，，则           。A. B. C. D.【答案】C【解析】 ,选C.9．已知角的始边是轴非负半轴．其终边经过点，则的值为__________．【答案】【解析】由题意得:,且 ,故填.10．在平面直角坐标系中，角的顶点与原点重合，始边与x的非负半轴重合，终边过点，则______________。【答案】；【解析】由题意，角的终边过点，求得，利用三角函数的定义，求得，又由.11．  平面直角坐标系中，点是单位圆在第一象限内的点，，若，则为_____．【答案】【解析】由题意知：，，由，得， ，故答案为：.12．若，则（  ）【答案】【解析】由题意得，，则.，故选.13．已知，则的值为            。【答案】【解析】因为，所以，14．已知均为锐角，满足，则        。【答案】【解析】由已知α、β均为锐角，，，又cos（α+β）＝cosαcosβ﹣sinαsinβ＝，∵0＜α+β＜π，∴α+β＝．15．若，则         。【答案】【解析】令，则由，可得16．已知，，则________.【答案】.【解析】∵，，平方相加可得即由降幂公式可得求得.17．若，则________．【答案】【解析】由题意，，通分可得，，，，所以本题答案为.18．  已知，则__________．【答案】【解析】因为，所以，应填答案。19．若，则________．【答案】【解析】，则，故答案为.20．若，则________.【答案】【解析】由题意可得：，即：，解方程可得：.21．已知α∈，β∈，且cos＝，sin＝－，则cos(α＋β)＝________.【答案】　－【解析】　∵α∈，∴－α∈，又cos＝，∴sin＝－，∵sin＝－，∴sin＝，又∵β∈，＋β∈，∴cos（＋β）＝，∴cos(α＋β)＝cos[-]＝coscos＋sinsin＝×－×＝－.22．（1）已知，求的值；（2）已知，求的值.【解析】（1）由题得.（2）,所以.23．已知是方程的根， 是第三象限角.（1）求 的值；（2）已知，若是第三象限角，且，求的值.【解析】(1)∵方程5x2－7x－6＝0的根为或2，又是第三象限角，∴sin＝，∴cos＝－＝，，∴原式.(2).，又α是第三象限角，.故.24．已知关于x的方程2x2－(＋1)x＋m＝0的两根分别是sin θ和cos θ，θ∈(0,2π)，求：(1)＋的值；(2)m的值；(3)方程的两根及此时θ的值． 【解析】(1)原式＝＋＝＋＝＝sin θ＋cos θ.由条件知sin θ＋cos θ＝，故＋＝.(2)由已知，得sin θ＋cos θ＝，sin θcos θ＝，因为1＋2sin θcos θ＝(sin θ＋cos θ)2，所以1＋2×＝2，解得m＝.(3)由得或又θ∈(0,2π)，故θ＝或θ＝.故当sin θ＝，cos θ＝时，θ＝；当sin θ＝，cos θ＝时，θ＝.25.已知函数f(x)＝sin2x－cos2x－2sin xcos x(x∈R)．(1)求f的值；(2)求f(x)的最小正周期及单调递增区间．【解析】(1)由题意，故(2)由(1)知，，则f(x)的最小正周期是π。由正弦函数的性质，令，解得，所以f(x)的单调递增区间是