2021-2022学年高一数学下学期期末考试仿真模拟卷（苏教版2019必修第二册）（七）

2021-2022学年高一数学下学期期末考试仿真模拟卷（苏教版2019必修第二册）（七）

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1.在中，，，则（    ）

A.  B.

C.  D.

【答案】A

【解析】如图所示：

因为，，所以，

 故选：A

2.从一批产品中取出三件产品，设为“三件产品全不是次品”，为“三件产品全是次品”，为“三件产品至少有一件是次品”，则下列结论正确的是（    ）

A. 任何两个均不互斥 B. 任何两个均互斥

C. 与互斥 D. 与互斥

【答案】D

【解析】由题知：表示“三件产品全是正品”；表示“三件产品全是次品”，

表示“三件产品一件次品，二件正品”，“三件产品两件次品，一件正品”，

“三件产品全是次品”，三种情况.

所以与互斥，与互斥，与不互斥.

故选项A，B C错误，D正确.  故选：D

3.在等腰梯形中，，，.将等腰梯形绕所在直线旋转一周而形成的曲面所围成的几何体的体积为（    ）

A.  B.  C.  D.

【答案】C

【解析】由题意可知旋转后的几何体如图：

将等腰梯形绕所在直线旋转一周而形成的曲面

所围成的几何体的体积为

圆柱的体积减去两个相同圆锥的体积

，   故选：C

4.袋中装有外形相同的四个小球，四个球上分别标有2，3，4，6四个数，现从袋中随机取出两个球，则两球上数字之差的绝对值不小于2的概率为（    ）

A.  B.  C.  D.

【答案】C

【解析】现从袋中随机取出两个球，基本事件总数n＝6，

两球上数字之差的绝对值不小于2包含的基本事件有：

（2，4），（2，6），（3，6），（4，6），共4个，

∴两球上数字之差的绝对值不小于2的概率为p＝．故选：C．

5.已知，，则等于（    ）

A． B． C． D．

【答案】B

【解析】，故，

由，解得，

故，故选：B

6.已知向量，向量，则的最大值，最小值分别是（    ）

A. ，0 B. 4， C. 16，0 D. 4，0

【答案】D

【解析】向量，向量，则2（2cosθ，2sinθ+1），

所以|22＝（2cosθ）2+（2sinθ+1）2＝8﹣4cosθ+4sinθ＝8﹣8sin（），

所以|22的最大值，最小值分别是：16，0；

所以|2的最大值，最小值分别是4，0；故选：D．

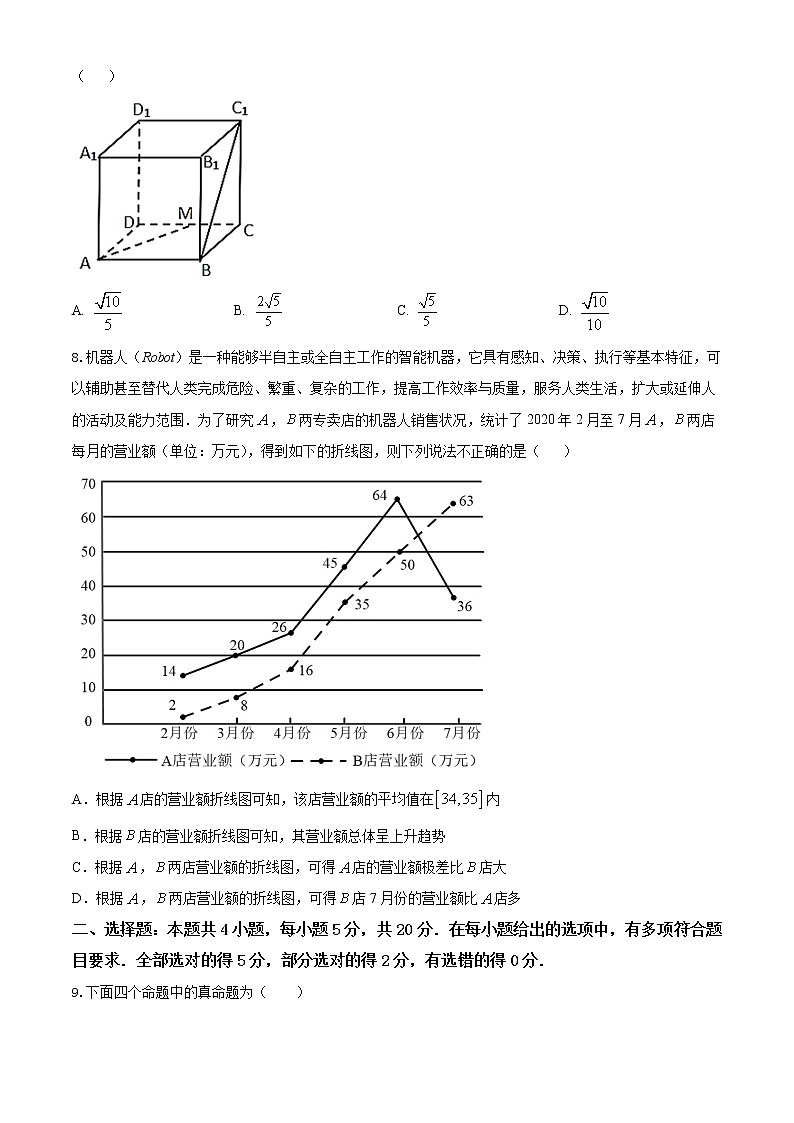
7.如图，点M是正方体ABCD-A1B1C1D1的棱CD的中点，则异面直线AM与BC1所成角的余弦值是（    ）

A.  B.  C.  D.

【答案】A

【解析】连接，，如图：

易得，所以（或其补角）是异面直线AM与BC1所成角，

设正方体的棱长为，，，

在三角形中，，

所以异面直线AM与BC1所成角的余弦值是.  故选：A

8.机器人（Robot）是一种能够半自主或全自主工作的智能机器，它具有感知、决策、执行等基本特征，可以辅助甚至替代人类完成危险、繁重、复杂的工作，提高工作效率与质量，服务人类生活，扩大或延伸人的活动及能力范围．为了研究，两专卖店的机器人销售状况，统计了2020年2月至7月，两店每月的营业额（单位：万元），得到如下的折线图，则下列说法不正确的是（    ）

A．根据店的营业额折线图可知，该店营业额的平均值在内

B．根据店的营业额折线图可知，其营业额总体呈上升趋势

C．根据，两店营业额的折线图，可得店的营业额极差比店大

D．根据，两店营业额的折线图，可得店7月份的营业额比店多

【答案】ABD

【解析】

根据店的营业额折线图可知，

该店营业额的平均值为，故A正确；

根据店的营业额折线图可知，其营业额总体呈上升趋势，故B正确；

店营业额的极差为，店营业额的极差为，

故店营业额的极差比店小，故C错误；

由折线图可知，店7月份的营业额比店多，故D正确．  故选：C．

二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

9.下面四个命题中的真命题为（    ）

A．若复数满足，则

B．若复数满足，则

C．若复数，满足，则

D．若复数，则

【答案】AD

【解析】若复数满足，则，故命题为真命题；

复数满足，则，故命题为假命题；

若复数，满足，但，故命题为假命题；

若复数，则，故命题为真命题.

故选AD。

10.给出下列结论，其中真命题为（    ）

A. 若，，则

B. 向量、为不共线的非零向量，则

C. 若非零向量、满足，则与垂直

D. 若向量、是两个互相垂直的单位向量，则向量与的夹角是

【答案】CD

【解析】对于A，若，，则或，所以该命题是假命题；

对于B，，而，

由于、为不共线的非零向量，所以，所以，

所以该命题是假命题；

对于C，若非零向量、满足，，所以，则与垂直，所以该命题是真命题；

对于D，以与为邻边作平行四边形是正方形，则和所在的对角线互相垂直，所以向量与的夹角是，所以该命题是真命题.  故选：CD.

11.在中，已知，且，则（    ）

A． B．

C．若，则 D．

【答案】BC

【解析】因为，

所以，即.

又因为，

所以，

即，.

对选项A，因为，故A错误.

对选项B，因为，，所以，

即，故B正确.

对选项C，若，则，，

则，

因为，所以.

故，故C正确.

对选项D，若.

又因为，则.

因为，设，，，，

则，故D错误.    故选BC。

12.如图,正方形中,分别是的中点将分别沿折起,使重合于点.则下列结论正确的是（  ）

A．

B．平面

C．二面角的余弦值为

D．点在平面上的投影是的外心

【答案】ABC

【解析】对于A选项，作出图形，取EF中点H，连接PH，DH，又原图知和为等腰三角形，故,，所以平面，所以，故A正确；根据折起前后，可知三线两两垂直，于是可证平面，故B正确；根据A选项可知 为二面角的平面角，设正方形边长为2，因此，，，，由余弦定理得：，故C正确；由于，故点在平面上的投影不是的外心，即D错误；故选：ABC.

三、填空题：本题共4小题，每小题5分，共20分．

13.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果，哥德巴赫猜想的内容是：每个大于2的偶数都可以表示为两个素数的和，例如，在不超过14的素数中随机选取两个不同的数，其和等于14的概率为_______________

【答案】

【解析】不超过14的素数有2，3，5，7，11，13共6 个，从这6个素数中任取2个，有2与3，2与5，2与7，2与11，2与13，3与5，3与7，3与11，3与13，5与7，5与11，5与13，7与11，7与13，11与13共15种结果，其中和等于14的只有一组3与11，所以在不超过14的素数中随机选取两个不同的数，其和等于14的概率为,  故答案为:

14.若，则__________.

【答案】

【解析】由可以得到，

所以，设，则

则，

所以.   故答案为:.

15.在直角边长为3的等腰直角中，E、F为斜边上的两个不同的三等分点，则______.

【答案】4

【解析】设是接近的一个三等分点，

则，

，

又，

故答案为：.

16.在三棱锥中，底面，，，，则此三棱锥外接球的表面积为______．

【答案】

【解析】

由题可知两两垂直，可以把三棱锥延伸至以为长、宽、高的长方体中，且进而此三棱锥与该长方体共外接球，通过长方体可以求得外接球半径为（设外接球半径为，表面积为S）：

，所以.

故答案为：.

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

17.已知复数，(，i是虚数单位).

（1）若虚数是实系数一元二次方程的根，求实数m的值;

（2）若在复平面内对应的点落在第一象限，求实数a的取值范围.

【答案】（1）；（2）

【解析】（1）由得，即

，

所以，解得.

（2）由题意得，，

因为在复平面内对应的点落在第一象限，所以，解得.

18.已知.

（1）若，求向量在向量方向的投影的数量.

（2）若，且，求向量的坐标.

【答案】（1）；（2）或．

【解析】（1）因为，所以．

由展开得，，即，

解得，故向量在向量方向的投影的数量为．

（2）因为，所以，设，则

，解得或，故向量的坐标为或．

19.甲､乙两队举行围棋擂台赛，规则如下：两队各出3人，排定1，2，3号.第一局，双方1号队员出场比赛，负的一方淘汰，该队下一号队员上场比赛.当某队3名队员都被淘汰完，比赛结束，未淘汰完的一方获胜.如图表格中，第m行､第n列的数据是甲队第m号队员能战胜乙队第n号队员的概率.

（1）求甲队2号队员把乙队3名队员都淘汰的概率；

（2）比较第三局比赛，甲队队员和乙队队员哪个获胜的概率更大一些？

【答案】（1）；（2）甲队队员获胜的概率更大一些.

【解析】（1）甲队2号队员把乙队3名队员都淘汰的概率为

（2）第3局比赛甲队队员获胜可分为3个互斥事件

（i）甲队1号胜乙队3号，概率为；

（ii）甲队2号胜乙队2号，概率为；

(iii)甲队3号胜乙队1号，概率为

故第3局甲队队员胜的概率为.

则第3局乙队队员胜的概率为

因为，

故甲队队员获胜的概率更大一些．

20.如图，在三棱锥中，，，，D为线段AC的中点，E为线段PC上一点.

（1）求证：；

（2）求证：平面BDE⊥平面PAC.

【答案】（1）证明见解析； （2）证明见解析.

【解析】（1）由，，且平面，平面，且，

由线面垂直的判定定理，可得平面，

又因为平面，所以；

（2）由，为的中点，可得，

又由平面，平面，

所以平面平面，

又因为平面平面平面，且，

所以平面，

因为平面，所以平面平面

21.某校从参加高三模拟考试的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六组[90，100），[100，110），…，[140，150]后得到如下部分频率分布直方图，观察图形的信息，回答下列问题：

（1）求分数在[120，130）内的频率；

（2）若在同一组数据中，将该组区间的中点值（如：组区间[100，110）的中点值为=105）作为这组数据的平均分，据此，估计本次考试的平均分；

（3）用分层抽样的方法在分数段为[110，130）的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任取2人，求至多有1人在分数段[120，130）内的概率．

【答案】（1）0.3; （2）121;（3）.

【解析】（1）分数在[120，130）内的频率为

1﹣（0.1+0.15+0.15+0.25+0.05）=1﹣0.7=0.3；

（2）估计平均分为

=95×0.1+105×0.15+115×0.15+125×0.3+135×0.25+145×0.05=121；

（3）依题意，[110，120）分数段的人数为60×0.15=9（人），

[120，130）分数段的人数为60×0.3=18（人）；

∵用分层抽样的方法在分数段为[110，130）的学生中抽取一个容量为6的样本，

∴需在[110，120）分数段内抽取2人，并分别记为m，n；

在[120，130）分数段内抽取4人，并分别记为a，b，c，d；

设“从样本中任取2人，至多有1人在分数段[120，130）内”为事件A，

则基本事件有（m，n），（m，a），…，（m，d），（n，a），…，（n，d），（a，b），…，（c，d）共15种；

则事件A包含的基本事件有（m，n），（m，a），（m，b），（m，c），（m，d），（n，a），（n，b），（n，c），（n，d）共9种；

∴P（A）．

22.在中，角A，B，C的对边分别是a，b，c，且.

（1）求角A的大小；

（2）求的取值范围.

【答案】（1）；（2）.

【解析】（1）由正弦定理可得，，

从而可得，，

即，又B为三角形的内角，

所以，于是，

又A为三角形内角，因此，.

（2）∵

，

由可知，，所以，

从而，

因此，，

故的取值范围为.