新高考数学实战演练仿真模拟卷5（带答案）

新高考数学实战演练仿真模拟卷5

一．选择题（共8小题）

1．复数在复平面内对应的点为，为虚数单位），则复数的虚部为　　

A． B． C． D．

【解析】解：根据题意，，且，

，

的虚部为．

故选：．

2．已知集合或，，则　　

A． B． C． D．

【解析】解：集合或，，

，

则，

故选：．

3．《周髀算经》是我国古老的天文学和数学著作，其书中记载：一年有二十四个节气，每个节气晷长损益相同（晷是按照日影测定时刻的仪器，晷长即为所测影子的长度），夏至、小暑、大暑、立秋、处暑、白露、秋分、寒露、霜降是连续的九个节气，其晷长依次成等差数列，经记录测算，这九个节气的所有晷长之和为49.5尺，夏至、大暑、处暑三个节气晷长之和为10.5尺，则立秋的晷长为　　

A．1.5尺 B．2.5尺 C．3.5尺 D．4.5尺

【解析】解：夏至、小暑、大暑、立秋、处暑、白露、秋分、寒露、霜降是连续的九个节气，其晷长依次成等差数列，

经记录测算，这九个节气的所有晷长之和为49.5尺，夏至、大暑、处暑三个节气晷长之和为10.5尺，

，，即．

解得，．

立秋的晷长．

故选：．

4．已知函数是定义在上的奇函数，且在上单调递减，，则不等式的解集为　　

A． B．，， 

C．，， D．，，

【解析】解：根据题意，函数是定义在上的奇函数，且在上单调递减，

则在上递减，

又由，则（3），则函数的草图如图：

若，则有，解可得，

即不等式的解集为，，；

故选：．

5．已知两点，，动点在直线上运动，则的最小值为　　

A． B． C．4 D．5

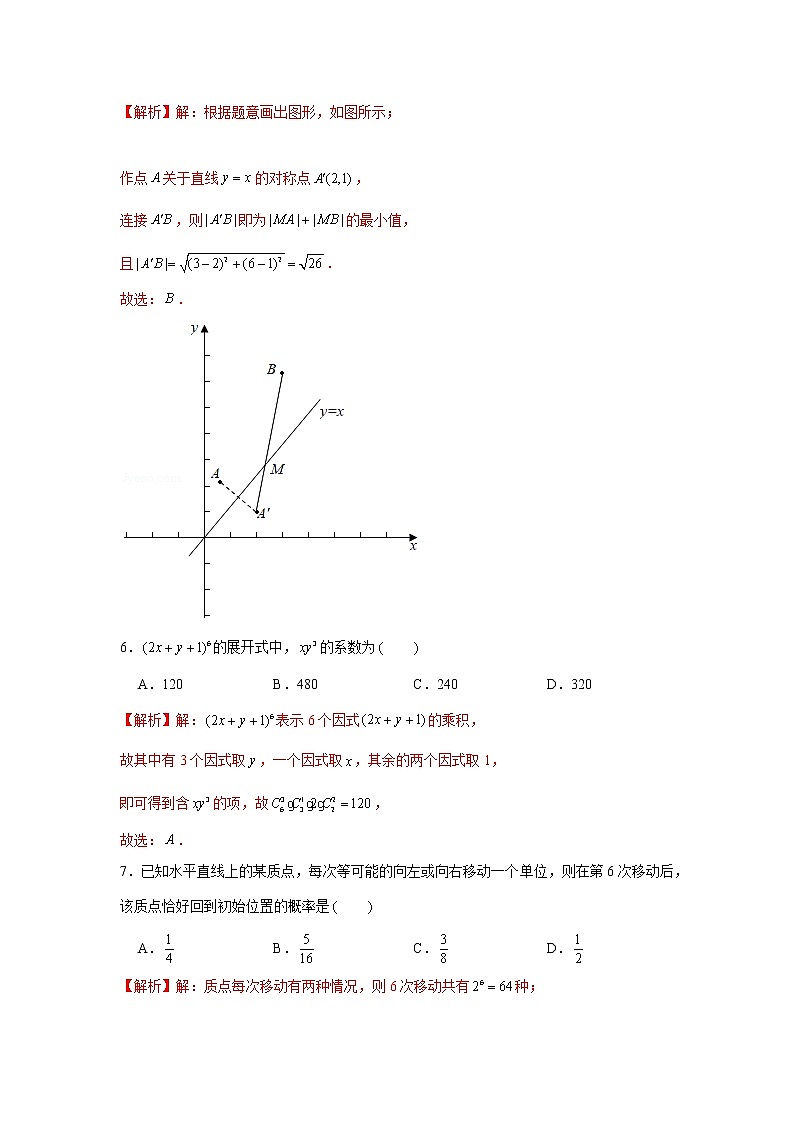
【解析】解：根据题意画出图形，如图所示；

作点关于直线的对称点，

连接，则即为的最小值，

且．

故选：．

6．的展开式中，的系数为　　

A．120 B．480 C．240 D．320

【解析】解：表示6个因式的乘积，

故其中有3个因式取，一个因式取，其余的两个因式取1，

即可得到含的项，故，

故选：．

7．已知水平直线上的某质点，每次等可能的向左或向右移动一个单位，则在第6次移动后，该质点恰好回到初始位置的概率是　　

A． B． C． D．

【解析】解：质点每次移动有两种情况，则6次移动共有种；

若6次移动后回到原位置，说明6次移动有3次向左，3次向右共有种，

则质点恰好回到初始位置的概率．

故选：．

8．若函数在区间，上不是单调函数，则实数的取值范围是　　

A． B． C． D．

【解析】解：函数的导数

若在区间，上不是单调函数，

则在区间，上有解，

即在区间，上有解（变号解），

即，

则，（此处千万不能取等号）

故选：．

二．多选题（共4小题）

9．已知函数，其导函数为，则　　

A． B． C． D．

【解析】解：，，

，，

．

故选：．

10．下列选项中，正确的有　　

A．若，都是第一象限角，且，则 

B．函数的最小正周期是 

C．若是定义在上的奇函数，且最小正周期是，则 

D．函数的最小值为

【解析】解：，都是第一象限角，且，取，，可得，所以不正确；

函数的图象如图：

不是周期函数，所以不正确；

若是定义在上的奇函数，且最小正周期是，则，因为，

所以，所以正确；

函数，当时，函数取得最小值．

故选：．

11．已知函数，的最小正周期为，且，则的值可以为　　

A． B． C． D．

【解析】解：由题意得，，因为，所以直线为函数图象的一条对称轴，所以，．

因为，所以或．

故选：．

12．已知函数，其导函数为，下列命题中为真命题的是　　

A．的单调减区间是， 

B．的极小值是 

C．过点只能作一条直线与的图象相切 

D．有且只有一个零点

【解析】解：，

令，解得：或，令，解得：，

则在递增，在，递减，在递增，

故（1），，

故只有1个零点，故错误，正确，

过点只能作1条直线与的图象相切，

设切点为，，，，

故切线方程是，

将代入得：，

令，则，

故在，，递增，在递减，

，，

故方程只有1个解，

即过点只能作一条直线与的图象相切，

故正确，

故选：．

三．填空题（共4小题）

13．2018年5月至2019年春，在阿拉伯半岛和伊朗西南部，沙漠蚂虫迅速繁衍，呈现几何式的爆发，仅仅几个月，蝗虫数量增长了8000倍，引发了蝗灾，到2020年春季蝗灾已波及印度和巴基斯坦，假设蝗虫的日增长率为，最初有只．则经过　199　天能达到最初的16000倍（参考数据：，，，．

【解析】解：设过天能达到最初的16000倍，由已知，

即，

所以，

又，所以过199天能达到最初的16000倍，

故答案为：199．

14．双曲线的左、右焦点分别为、，过且斜率为的直线与双曲线的左、右两支分别交于点、在右侧），若，则的离心率为　．　．

【解析】解：由，

得，

由双曲线定义得，，

．

由直线的斜率为，得．

在△中，由余弦定理得，

解得（舍去），或．

故答案为：．

15．已知函数，若存在实数，满足，且，则的最大值为　　．

【解析】解：根据题意得，，，即，

又，，此时，

构造函数，可得，

函数在，上单调递增，

即（e）．

故答案为：．

16．在数列中，，且，则数列的前2021项和为　　．

【解析】解：由且，变形为：，

，

数列是等比数列，首项为，公比为3．

，

．

数列的前2021项和．

故答案为：．

四．解答题（共6小题）

17．已知函数只能同时满足下列三个条件中的两个：

①函数的最大值为2；②函数的图象可由的图象平移得到；③函数图象的相邻两条对称轴之间的距离为．

（1）请写出这两个条件序号，并求出的解析式；

（2）求方程在区间，上所有解的和．

【解析】解：（1）函数满足条件为①③：

理由如下：由题意可知条件①②互相矛盾，

故③为函数满足的条件之一．

由③可知：，所以．

故②不合题意．

所以函数满足条件为①③：

由①知：．

所以．

（2）由于．

所以，

所以或，

解得：或，

由于，，

所以的取值为．

所以方程的所有的解的和为．

18．已知数列的前项和为，，且．

（1）求数列的通项公式；

（2）设，数列的前项和为，求．

【解析】解：（1）由题意，可知

当时，，

当时，，

数列是以3为首项，1为公差的等差数列，

故，

，，

则当时，

，

当时，也满足上式，

，，

（2）由（1），可得

，

，

，

两式相减，可得

，

令，则

，

两式相减，可得

，

，

，

．

19．如图，四棱锥中，底面为矩形，侧面为正三角形，且平面平面，为中点，．

（1）求证：平面平面；

（2）若二面角的平面角大小满足，求线段的长．

【解析】解：（1）取的中点，

侧面为正三角形，，

又平面平面，平面，平面平面，平面，

如图所示，以为原点，建立空间直角坐标系，设，则，0，，，，，，0，，，0，，，0，，

，，，

，即，，

、平面，且，平面，

又平面，平面平面．

（2）由（1）可知，，，平面的法向量为，

设平面的法向量为，则，即，

令，则，，，

，

由题可知，二面角的平面角为锐角，

，解得或（舍负），

线段的长为．

20．在全球抗击新冠肺炎疫情期间，我国医疗物资生产企业加班加点生产口罩．防护服、消毒水等防疫物品，保障抗疫一线医疗物资供应，在国际社会上赢得一片赞誉．我国某口罩生产厂商在加大生产的同时，狠抓质量管理，不定时抽查口罩质量，该厂质检人员从某日所生产的口罩中随机抽取了100个，将其质量指标值分成以下五组：，，，，，，，，，，得到如图频率分布直方图．

（1）规定：口罩的质量指标值越高，说明该口罩质量越好，其中质量指标值低于130的为二级口罩，质量指标值不低于130的为一级口罩．现从样本口罩中利用分层抽样的方法随机抽取8个口罩，再从中抽取3个，记其中一级口罩个数为，求的分布列及数学期望；

（2）在2020年“五一”劳动节前，甲计划在该型号口罩的某网络购物平台上参加店一个订单“秒杀”抢购，同时乙计划在该型号口罩的某网络购物平台上参加店一个订单“秒杀”抢购，其中每个订单均由个该型号口罩构成．假定甲、乙两人在，两店订单“秒杀”成功的概率均为，记甲，乙两人抢购成功的订单总数量、口罩总数量分别为，．

①求的分布列及数学期望；

②当的数学期望取最大值时正整数的值．

【解析】解：（1）按分层抽样抽取8个口罩，则其中二级、一级口罩个数分别为6，2．

故的可能取值为0，1，，，，

所以．

（2）①由题知，的可能取值为0，1，2，，，

所以．

②因为，所以，

当且仅当时取等号，所以取最大值时，的值为2．

21．已知椭圆的离心率为，以原点为圆心，椭圆的短半轴长为半径的圆与直线相切．

（1）求椭圆的方程；

（2）设，过点作与轴不重合的直线交椭圆于，两点，连接，分别交直线于，两点，若直线、的斜率分别为、，试问：是否为定值？若是，求出该定值，若不是，请说明理由．

【解析】解：（1）由题意得，，

以原点为圆心，椭圆的短半轴长为半径的圆与直线相切，可得

，解得，，，

故椭圆的方程为；

（2）设，，，，

直线的方程为，代入椭圆方程，

得，

，，

由，，三点共线可知，，即；

同理可得．

所以．

因为，

所以

．

即为定值．

22．设，．

（1）讨论在，上的单调性．

（2）令，试证明在上有且仅有三个零点．

【解析】解：（1），

令，则，或，

时，，单调递增，

时，，单调递减，

时，，单调递增，

时，，单调递减，

证明：（2），则，

故是的一个零点，

即是偶函数，

要确定在上的零点个数只需确定时，的零点个数即可，

①当时，，

令，即，，

时，，单调递减，，

时，，单调递增，，

在有唯一零点．

②当时，由于，，，

而在单调递增，，故，

故在无零点，

在有一个零点，

由于是偶函数，在有一个零点，而，

故在上有且仅有3个零点